Hình thoi là gì? Tính chất và cách nhận biết hình thoi?

1. Hình thoi là gì?

Hình thoi là hình tứ giác có bốn cạnh bằng nhau, là hình bình hành có hai cạnh liền kề bằng nhau hoặc có đường chéo vuông góc với nhau.

Ví dụ: Tứ giác ABCD là hình thoi <=> AB=BC=CD=DA.

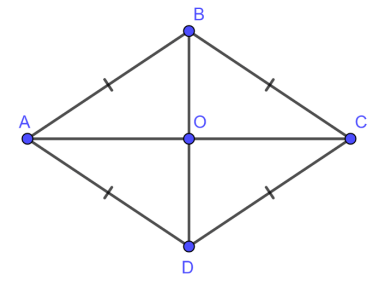
Hình thoi cũng chính là hình bình hành đặc biệt.

2. Tính chất của hình thoi:

Trong một hình thoi có những tính chất sau đây:

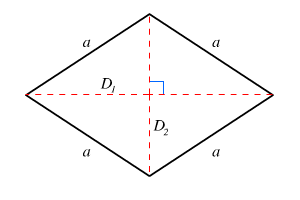
– Có các góc đối diện bằng nhau.

– Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.

– Hai đường chéo chia các góc hình thoi thành hai góc bằng nhau (đường phân giác).

– Hình thoi có tất cả các tính chất của hình bình hành (có cạnh đối song song và bằng nhau; có các góc đối bằng nhau; hai đường chéo cắt nhau tại trung điểm mỗi đường).

3. Dấu hiệu nhận biết của hình thoi:

– Hình thoi là hình tứ giác đặc biệt:

+ Hình thoi là hình tứ giác có bốn cạnh bằng nhau.

+ Hình thoi là hình tứ giác có hai đường chéo là đường phân giác của cả bốn góc.

+ Hình thoi là hình tứ giác có hai đường chéo là đường trung trực của nhau.

– Hình thoi là hình bình hành đặc biệt:

Do hình thoi là một dạng đặc biệt của hình bình hành nên sẽ bao gồm tất cả tính chất của hình bình hành, ngoài ra có thêm một số tính chất khác như:

+ Hình bình hành có hai cạnh bên bằng nhau là hình thoi.

+ Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

+ Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

4. Công thức tính chu vi hình thoi:

Chu vi của hình thoi bằng độ dài của một cạnh nhân với 4.

P = a x 4.

Trong đó:

P : Chu vi

a : Độ dài của 1 cạnh.

Ví dụ: Cho hình thoi có độ dài các cạnh bằng 5 (cm). Hãy tính chu vi của hình thoi.

Giải: Chu vi của hình thoi là:

P = a x 4 = 5 x 4 = 20 (cm).

5. Công thức tính diện tích của hình thoi:

Diện tích hình thoi bằng một nửa tích độ dài của hai đường chéo.

S = 1/2 x d1 x d2 = h x a.

Trong đó:

S: Diện tích hình thoi.

d1, d2: hai đường chéo hình thoi.

h: chiều cao của hình thoi.

a: độ dài cạnh của hình thoi.

Ví dụ: Cho hình thoi có hai đường chéo lần lượt là 3cm và 6cm. Hãy tính diện tích của hình thoi đó.

Giải: S = 1/2 x d1 x d2 = 1/2 x 3 x 6 = 9 (cm).

6. Một số bài tập vận dụng:

Bài 1: Hãy chọn câu sai. Để nhận biết một tứ giác là hình thoi ta có các cách sau:

A. Tứ giác có bốn cạnh bằng nhau.

B. Tứ giác có hai đường chéo vuông góc và bằng nhau.

C. Hình bình hành có một đường chéo là phân giác của một góc.

D. Hình bình hành có hai đường chéo vuông góc.

Đáp án: B. Vì A, C, D là dấu hiệu nhận biết của hình thoi.

Bài 2: Hình thoi có chu vi bằng 16cm thì cạnh của nó bằng bao nhiêu?

A. 2cm.

B. 4cm.

C. 8cm.

D. Cả A, B, C đều sai.

Đáp án: B. Dựa vào công thức tính chu vi của hình thoi nên ta có cạnh của hình thoi là 16 : 4 = 4 (cm).

Bài 3: Hình thoi có độ dài hai đường chéo lần lượt bằng 12cm và 16cm. Độ dài cạnh hình thoi đó là:

A. 14cm.

B. 28cm.

C. 100cm

D. 10cm.

Đáp án: D.

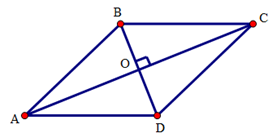
Giả sử hình thoi ABCD có hai đường chéo AC = 16cm, BD = 12cm cắt nhau tại O.

Theo tính chất hình thoi ta có AC vuông góc với BD, O là trung điểm của AC, BD.

Do đó: OA = 1/2 AC = 16 : 2 = 8 (cm); OB = 1/2 BD = 12 : 2 = 6 (cm).

Áp dụng định lý Pytago cho tam giác ABO vuông tại O ta có:

AB² = OA² + OB² = 6² = 8² = 100 => AB = 10 (cm).

Vậy độ dài cạnh hình thoi là 10cm.

Bài 4: Trong các khẳng định sau, khẳng định nào sai đối với hình thoi:

A. Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

B. Hai đường chéo là các đường phân giác của các góc của hình thoi.

C. Hai đường chéo bằng nhau.

D. Hai đường chéo vuông góc với nhau.

Đáp án: C. Dựa vào tính chất của hình thoi.

Bài 5: Tập hợp tất cả các điểm cách đều đường thằng a cố định một khoảng bằng 2,5cm là:

A. Tia phân giác của góc aOb.

B. Hai đường thằng song song với a và cách a một khoảng bằng 2,5cm.

C. Đường tròn tâm O bán kính 2,5cm.

D. Đường trung trực của đoạn thẳng AB.

Đáp án: B. Tập hợp tất cả các điểm cách đều đường thẳng a cố định một khoảng bằng 2,5cm là hai đường thẳng song song với a và cách a một khoảng bằng 2,5cm.

Bài 6: Cho điểm M trong hình chữ nhật ABCD có AB bằng 10cm và AD bằng 6cm. Trong đó, M cách AB một khoảng bằng 2cm, cách AD một khoảng bằng 4cm. Vậy khoảng cách từ M đến đỉnh C là bao nhiêu?

A. 26cm.

B. 52cm.

C. √26cm.

D. √52cm.

Đáp án: D.

Gọi H, K, I lần lượt là chân đường vuông góc kẻ từ M đến AB, AD, DC.

Ta có MI = AD – AK = AD – MH = 6 – 2 = 4.

IC = DC – DI = AB = KM = 10 – 4 = 6.

Áp dụng định lý Pytago cho tam giác MIC ta có:

MC²  = MI^{2 +} IC² = 4² + 6² = 52 cm.

=> MC = √52cm.

Bài 7: Cho hình chữ nhật ABCD, P, Q lần lượt là trung điểm của BC và AD. Gọi M là giao điểm của AP và BQ, N là giao điểm của CQ và DP. Chứng minh tứ giác MNPQ là hình thoi.

Giải:

Ta có P, Q lần lượt là trung điểm của AD và BC nên AQ = QD = BP = PC.

Ta lại có AQ // CP, DQ // BP.

Do đó các tứ giác APCQ và BPDQ là hình bình hành.

AP // CQ, BQ // DP

MNPQ là hình bình hành.

Mặt khác tứ giác ABPQ là hình chữ nhật do AQ // BP, AQ = BP.

Vậy MNPQ là hình thoi.

Bài 8:  Cho hình bình hành ABCD có AB = AC. Kéo dài trung tuyến AM của tam giác ABC lấy ME = MA.

a) Chứng minh tứ giác ABEC là hình thoi.

b) Chứng minh C là trung điểm của DE.

Giải:

a) Ta có MB = MC, MA = ME nên tứ giác ABEC là hình bình hành. (1)

Mặt khác cân có trung tuyến AM đồng thời là đường cao hay (2)

Từ (1) và (2) suy ra ABEC là hình thoi.

b) Ta có CD // AB, CE // AB

CE và CD trùng nhau. Vậy C, D, E thẳng hàng.

ABEC là hình thoi (3)

ABCD là hình bình hành (4)

Từ (3), (4) suy ra CD = CE hay C là trung điểm của DE.

7. Một số bài tập tự luyện:

Bài 1: Cho tam giác ABC, phân giác AD. Qua D kẻ đường thẳng song song với AC cắt AB tại E, qua D kẻ đường thẳng song song với AB cắt AC tại F. Chứng minh È là phân giác của góc AED.

Bài 2: CHo tam giác ABC cân tại A, trung tuyến AM. Qua M kẻ đường thẳng song song với AC cắt AB tại P và đường thẳng song song với AB cắt AC tại Q.

a) Tứ giác APMQ là hình gì? Vì sao?

b) Chứng minh PQ // BC.

Bài 3: Cho hình bình hành ABCD. Trên các cạnh của AB và CD lần lượt lấy các điểm M và N sao cho AM = DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F.

a) Chứng minh E và F đối xứng nhau qua AB.

b) Chứng minh tứ giác MEBF là hình thoi.

c) Hình bình hành ABCD có thêm điều kiện gì để tứ giác BCNE là hình thang cân.

Bài 4:  Cho hình bình hành ABCD, các đường chéo cắt nhau tại O. Gọi E, F, G, H theo thứ tự là giao điểm của các đường phân giác của các tam giác AOB, BOC, COD, DOA. Chứng minh EFGH là hình thoi.

Bài 5: Cho hình bình hành ABCD có AB = 2BC. Gọi M, N lần lượt là trung điểm của AB và CD.

a) Chứng minh tứ giác AMND là hình thoi.

b) Gọi E là giao điểm của AN và DM; F là giao điểm của BN và MC. Tứ giác MENF là hình gì? Vì sao?

Bài 6: Cho hình bình hành ABCD, hai đường chéo cắt nhau ở O. Hai đường thẳng d1 và d2 cùng đi qua O và vuông góc với nhau. Đường thẳng d1 cắt các cạnh AB và CD ở M và P. Đường thẳng d2 cắt các cạnh BC và AD ở N và Q. Chứng minh tứ giác MNPQ là hình thoi.