Hàm số chẵn là gì? Hàm số lẻ là gì? Xác định tính chẵn lẻ?

1. Hàm số chẵn là gì? 

Hàm số y = f (x) có tập xác định D gọi là hàm số chẵn nếu thoả mãn 2 điều kiện sau:

∀ x ∈ D ⇒ − x ∈ D

∀ x ∈ D : f ( − x ) = f ( x )

Ví dụ: Hàm số y = x² là hàm số chẵn

2. Hàm số lẻ là gì?

Hàm số y = f ( x ) có tập xác định D gọi là hàm số lẻ nếu thoả mãn 2 điều kiện sau:

∀ x ∈ D ⇒ − x ∈ D

∀ x ∈ D : f (−x)= − f(x)

Ví dụ: Ví dụ: Hàm số y = x là hàm số lẻ

Chú ý. Điều kiện thứ nhất gọi là điều kiện tập xác định đối xứng qua số 0.

Ví dụ D = (-2;2) là tập đối xứng qua số 0, còn tập D’ = [-2;3] là không đối xứng qua 0.

Tập R = (−∞;+∞) là tập đối xứng.

Chú ý: Một hàm số không nhất thiết phải là hàm số chẵn hoặc hàm số lẻ.

Ví dụ: Hàm số y = 2x + 1 không là hàm số chẵn, cũng không là hàm số lẻ vì:

Tại x = 1 có f(1) = 2.1 + 1 = 3

Tại x = -1 có f(-1) = 2.(-1) + 1 = -1

→ Hai giá trị f(1) và f(-1) không bằng nhau và cũng không đối nhau.

Đồ thị của hàm số chẵn, lẻ

– Hàm số chẵn có đồ thị nhận trục tung Oy làm trục đối xứng

– Hàm số lẻ có đồ thị nhận gốc tọa độ O là tâm đối xứng

3. Cách xác định tính chẵn lẻ:

3.1. Cách xác định tính chẵn lẻ bằng định nghĩa:

Để xét tính chẵn lẻ của hàm số các bạn cần sử dụng định nghĩa và quy trình xét hàm số chẵn, lẻ cụ thể như sau:

Cho hàm số $y$ xác định trên 

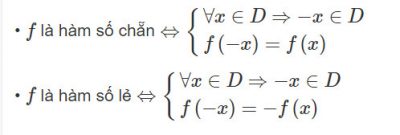
Các bước xét tính chẵn, lẻ của hàm số:

Bước 1. Tìm tập xác định  của hàm số.

Bước 2. Kiểm tra:

– Nếu $\forall x\in D$ thì chuyển qua bước 3.

– Nếu tồn tại $x_0\in D$ mà $-x_0\notin D$ thì kết luận hàm không chẵn cũng không lẻ.

Bước 3. Xác định $f(-x)\; và$so sánh với $f\left(x\right):$

– Nếu $f\left(-x\right)$ thì kết luận hàm số là chẵn.

– Nếu $f\left(-x\right)$thì kết luận hàm số là lẻ.

3.2. Cách xác định hàm số chẵn lẻ bằng máy tính:

Ý tưởng dùng Casio để xét dựa trên tổng giá trị f ( x ) và f ( – x ) bằng nhau hoặc đối nhau. Để triển khai ta dùng tính năng Table ở chính sách hai hàm số .

Ví dụ: Xét tính chẵn lẻ của hàm số y = x³ + 2 x² – 3

Giải: Trên máy tính cầm tay Vinacal 570 ES Plus II ta bấm như sau ( những máy tính bỏ túi khác bấm tương tự như ): MODE 7

Ta triển khai nhập hàm số đã cho trong đề bài

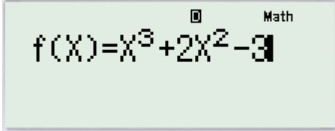
Tiếp theo ta nhập hàm số g ( x ) = f ( − x ) ( Tức là vị trí nào của x ta bấm − x )

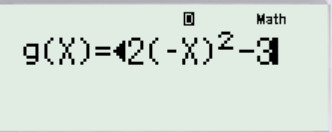
Các mục tiếp theo là START, END, STEP ta để mặc định cho nhanh (khả năng chọn cũng được). Ta được kết quả như sau:

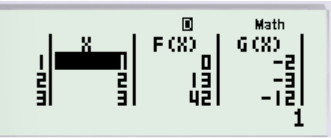
Đến đây ta dò hai cột tổng giá trị F ( X ) và G ( X ) thì thấy rằng tại x = 1 hai tổng giá trị không bằng nhau cũng không đối nhau. vì vậy hàm đã cho không phải hàm chẵn cũng không phải hàm lẻ. Lưu ý chiêu thức này mang tính ước đạt và không thay thế sửa chữa cho chứng tỏ được. mặc khác dùng trong giải toán trắc nghiệm năng lực dùng được .

4.  Ví dụ minh họa: 

Ví dụ 1: Xét tính chẵn lẻ của các hàm số sau:

a) y = |x|;

b) y = (x + 2)2;

c) y = x3 + x;

d) y = x2 + x + 1.

Hướng dẫn giải:

a) Đặt y = f(x) = |x|.

° TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.

° f(–x) = |–x| = |x| = f(x).

→ Vậy hàm số y = |x| là hàm số chẵn.

b) Đặt y = f(x) = (x + 2)2.

° TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.

° f(–x) = (–x + 2)² = (x – 2)² ≠ (x + 2)² = f(x)

° f(–x) = (–x + 2)² = (x – 2)² ≠ – (x + 2)² = –f(x).

→ Vậy hàm số y = (x + 2)² làm hàm số không chẵn, không lẻ.

c) Đặt y = f(x) = x3 + x.

° TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.

° f(–x) = (–x)3 + (–x) = –x3 – x = – (x3 + x) = –f(x)

→ Vậy y = x3 + x là hàm số lẻ.

d) Đặt y = f(x) = x2 + x + 1.

° TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.

° f(–x) = (–x)² + (–x) + 1 = x² – x + 1 ≠ x² + x + 1 = f(x)

° f(–x) = (–x)² + (–x) + 1 = x² – x + 1 ≠ –(x² + x + 1) = –f(x)

→ Vậy hàm số y = x2 + x + 1 là hàm số không chẵn, không lẻ.

Ví dụ 2: Xét tính chẵn lẻ của hàm số : y = f(x) = x³ + x

TXĐ : D = R

=> D là tập đối xứng.

lấy x ∈ D => – x ∈ D.

Xét f(-x) = (-x)³ + (-x) = -( x + x)= -f(x)

=> f(-x) = – f(x)

vậy : hàm số y = x3 + x là hàm số lẻ.

Bài tập minh họa: xét tính chẵn lẻ của các hàm số:

Bài 1: Chứng minh rằng với hàm số f(x) bất kỳ, f(x) có thể biểu diễn duy nhất dưới dạng tổng của một hàm số chẵn và một hàm số lẻ.

Bài 2: Cho hàm số y=f(x), y=g(x) có cùng tập xác định D. Chứng minh rằng:

Nếu hai hàm số trên lẻ thì hàm số y=f(x)+g(x) là hàm số lẻ.

Nếu hai hàm số trên một chẵn, một lẻ thì hàm số y=f(x)g(x) là hàm số lẻ.

Bài 3: Cho hàm số f(x) = (m – 2)x² + (m – 3)x + m² – 4

a) Tìm m để hàm f(x) là hàm chẵn

b) Tìm m để hàm f(x) là hàm lẻ.

Bài 4: Khảo sát tính chẵn lẻ của các hàm số có trị tuyệt đối sau

a) f(x) = |2x + 1| + |2x – 1|

b) f(x) = (|x + 1| + |x – 1|)/(|x + 1| – |x – 1|)

5. Xét tính chẵn lẻ của hàm số lượng giác: 

Phương pháp chung: Dựa vào định nghĩa hàm chẵn, hàm lẻ tương tự như chúng ta đã biết ở chương trình lớp 10. Chúng ta lần lượt thực hiện theo các bước sau:

Bước 1: Tìm tập xác định D của hàm số, khi đó:

+ Nếu D là tập đối xứng (tức ∀x ∈ D ⇒ -x ∈ D) ta chuyển qua bước 2

+ Nếu D không là tập đối xứng (tức là ∃x ∈ D mà –x ∉ D), ta kết luận hàm số không chẵn cũng không lẻ.

Bước 2: Thay x bằng –x và tính f(-x).

Bước 3: Kiểm tra (so sánh):

Nếu f(-x) = f(x) kết luận hàm số là hàm chẵn

Nếu f(-x) = -f(x) kết luận hàm số là hàm lẻ

Trường hợp khác kết luận hàm số không chẵn cũng không lẻ

Ví dụ:

Xét tính chẵn lẻ của các hàm số sau:

a. y = sinx.

b. y = cos(2x).

Hướng dẫn giải

a. Tập xác định D = R. Lấy x ∈ D thì – x ∈ D. Ta có: sin (-x) = -sinx. Vậy hàm số đã cho là hàm số lẻ.

b. Tập xác định D = R. Lấy x ∈ D thì – x ∈ D. Ta có: cos(-2x) = cos(2x). Vậy hàm số đã cho là hàm số chẵn.

Lưu ý:

1) Hàm số y = 0 vừa là hàm số chẵn, vừa là hàm số lẻ vừa là hàm hằng.

2) Khi xét tính chẵn lẻ của hàm số ta cần chú ý xét tập xác định đầu tiên để giải quyết bài toán
một cách chính xác.

3) Đồ thị hàm số lẻ thì đối xứng qua tâm O.

4) Đồ thị hàm số chẵn thì đối xứng qua trục Oy.

Tính chẵn lẻ của các hàm lượng giác cơ bản:

1. Hàm số y = sinx

– Là hàm số lẻ

– Có vô số tâm đối xứng: Ik(kπ; 0), k∈Z

2. Hàm số y = cosx

– Là hàm số chẵn

– Có vô số tâm đối xứng: x =kπ; k∈Z

3. Hàm số y = tanx

– Là hàm số lẻ

– Có vô số tâm đối xứng: Ik(kπ/2; 0), k∈Z

4. Hàm số y = cotx

– Là hàm số lẻ

– Có vô số tâm đối xứng: Ik(kπ/2; 0), k∈Z

Như vậy, trên đây là những thông tin cơ bản về hàm số chẵn, lẻ và cách tính hàm số chẵn, lẻ. Mong rằng những thông tin này giúp các bạn học sinh trong quá trình làm bài.