Số hữu tỉ là một khái niệm quan trọng trong toán học, thường được biểu diễn dưới dạng phân số a/b, với a và b là số nguyên, b≠0. Dưới đây là bài viết về chủ đề: Cách giải các dạng bài tập về số hữu tỉ lớp 7 hay nhất, mời bạn đọc theo dõi.
Mục lục bài viết
1. Cách giải các dạng bài tập về số hữu tỉ lớp 7 hay nhất:
Cộng, trừ hai số hữu tỉ
– Ta có thể cộng, trừ hai số hữu tỉ x, y bằng cách viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi áp dụng quy tắc cộng, trừ phân số
– Phép cộng số hữu tỉ có các tính chất của phép cộng phân số:
- Tính chất giao hoán
- Tính chất kết hợp
- Cộng với số 0
– Mỗi số hữu tỉ đều có một số đối.
Quy tắc “chuyển vế”
Khi chuyển vế một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó.
Nhân, chia hai số hữu tỉ
– Ta có thể nhân, chia hai số hữu tỉ bằng viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.
– Phép nhân số hữu tỉ có các tính chất của phép nhân phân số:
- Tính chất giao hoán
- Tính chất kết hợp
- Nhân với số 1
- Tính chất phân phối của phép nhân đối với phép cộng.
- Mỗi số hữu tỉ khác 0 đều có một số nghịch đảo
Cộng, trừ, nhân chia số thập phân
Để cộng, trừ, nhân, chia số thập phân, ta có thể viết chúng dưới dạng phân số thập phân rồi làm theo quy tắc các phép tính đã biết về phân số.
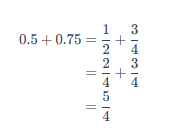
Lũy thừa với số mũ tự nhiên
Lũy thừa bậc n của một số hữu tỉ x, kí hiệu là , là tích của n thừa số x (n là một số tự nhiên lớn hơn 1)
Quy ước: 
Ví dụ: 2^{3}=2.2 .2 ; 3^{5}=3.3 .3 .3 .3
Tích và thương của hai lũy thừa cùng cơ số
(Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ)
(Khi chia hai lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia).
Lũy thừa của lũy thừa
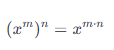(Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ.
Lũy thừa của một tích
(Lũy thừa của một tích bằng tích các lũy thừa)
Lũy thừa của một thương
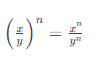(Lũy thừa của một thương bằng thương các lũy thừa)
Ví dụ: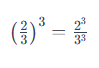
2. Lý thuyết về số hữu tỉ:
– Số hữu tỉ và tập hợp Q: Số hữu tỉ là một khái niệm quan trọng trong toán học, thường được biểu diễn dưới dạng phân số a/b, với a và b là số nguyên, b≠0. Tập hợp tất cả các số hữu tỉ được kí hiệu là Q.
– Biểu diễn trên trục số: Một đặc điểm quan trọng của số hữu tỉ là chúng có thể được biểu diễn trên trục số dưới dạng điểm. Điểm biểu diễn số hữu tỉ x trên trục số được gọi là điểm x. Việc này giúp chúng ta thấy rõ sự tương quan và khoảng cách giữa các số hữu tỉ.
– So sánh và phân loại số hữu tỉ: Với hai số hữu tỉ x và y, có ba trường hợp: x=y, x<y, hoặc x>y. Để so sánh chúng, ta có thể viết chúng dưới dạng phân số và so sánh các phân số tương ứng.
So sánh điểm trên trục số: Nếu x<y, trên trục số, điểm x sẽ ở bên trái điểm y, cho ta cái nhìn trực quan về sự so sánh giữa chúng.
Số hữu tỉ dương và âm: Số hữu tỉ lớn hơn 0 được gọi là số hữu tỉ dương, trong khi số nhỏ hơn 0 là số hữu tỉ âm. Sự phân biệt này không chỉ giúp xác định dấu của số mà còn gợi ý về vị trí của nó trên trục số.
Số 0 trong số hữu tỉ: Số 0 không thuộc phân loại số hữu tỉ dương cũng không là số hữu tỉ âm. Nó nằm ở trung tâm trên trục số, là điểm giao điểm của hai hướng số.
Ưu điểm của biểu diễn trên trục số: Biểu diễn số hữu tỉ trên trục số không chỉ là một cách hiệu quả để thể hiện sự liên quan giữa chúng mà còn mang lại sự hình dung và thị giác. Việc so sánh các số, xác định dấu, và quan sát vị trí trên trục số giúp học sinh phát triển sự hiểu biết sâu sắc về số hữu tỉ và cách chúng tương tác với nhau. Đồng thời, nó tạo ra một nền tảng cho việc học các khái niệm toán học phức tạp hơn trong tương lai.
3. Bài tập Số hữu tỉ có đáp án:
Bài tập 1: Tìm x ∈ Q biết : −25 + 56x = −415.
Lời giải:
−25 + 56x = −415
⇔ 56x = −415 − (−25)
⇔ 56x = −416 + 25
⇔ 56x = −390
⇔ x = -195/28
Bài tập 2: Thực hiện các phép tính sau:
a) (−35+511):(−37)+(−25+611):(−37)
b) (−25+14:−7101).(5517−47.23).(1−513:513).
Lời giải:
a) (−35+511):(−37)+(−25+611):(−37)
= (−35+511+−25+611):(−37)
= (−3−25+5+611):(−37) =0:(−37)=0.
b) (−25+14:−7101).(5517−47.23).(1−513:513)
= (−25+14:−7101).(5517−47.23).(1−1)
= (−25+14:−7101).(5517−47.23).0=0.
Bài tập 3: Tính giá trị các biểu thức sau:
B = −1/10−1/100−1/1000−1/10000−1/100000−1/1000000.
Lời giải:
B = −1/10−1/100−1/1000−1/10000−1/100000−1/1000000
= −(0,1+0,01+0,001+0,0001+0,00001+0,000001) = −0,111111.
Bài tập 4.
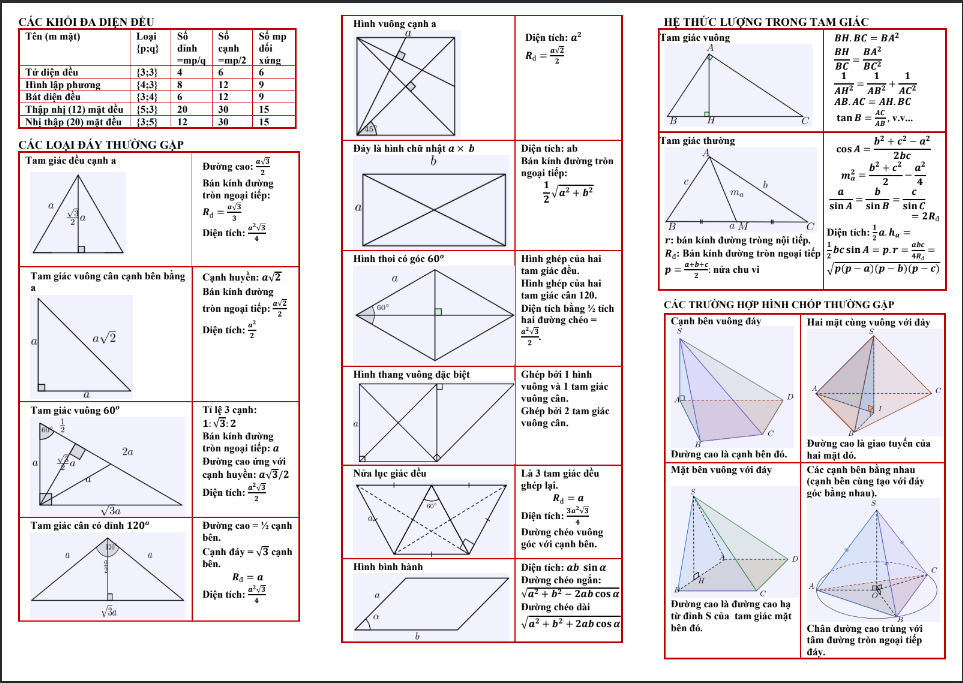
ZLời giải
Ta có:
2/3+4/5=10/15+12/15=22/15
Chọn đáp án A
Bài tập 5. Chọn kết luận đúng nhất về kết quả của phép tính -2/13+(-11)/26
A. Là số nguyên âm
B. Là số nguyên dương
C. Là số hữu tỉ âm.
D. Là số hữu tỉ dương.
Lời giải
Ta có:
-2/13+(-11)/26=(-4)/26+(-11)/26=(-15)/26
Là số hữu tỉ âm
Chọn đáp án C.
Bài tập 6: Số -3/14 là hiệu của hai số hữu tỉ nào dưới đây?
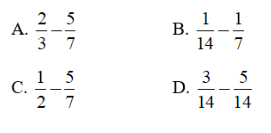
Lời giải
Ta có:
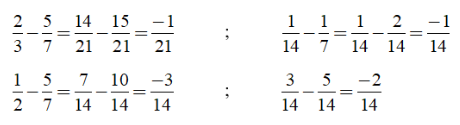
Chọn đáp án C.
Bài tập 7: Tìm x,y,z biết rằng: (x−15)(y+12)(z−3)= 0 Và x+1 = y+2 = z+3.
Lời giải
Ta có: (x−15)(y+12)(z−3)=0
⇔x−15=0 hoặc y+12=0 hoặc z−3=0
⇔x=15 hoặc y=−12 hoặc z=3
+ Nếu x=15, kết hợp với x+1=y+2=z+3 ta suy ra y=−45;z=−95
+ Nếu y=−12, kết hợp với x+1=y+2=z+3 ta suy ra x=12;z=−32
+ Nếu z=3, tương tự ta suy ra x=5;y=4
Vậy ta có ba bộ số thỏa mãn đó là:
15;−45;−95 hoặc 12;−12;−32 hoặc 5;4;3.
Bài tập 8: Tìm x∈Q biết: (23x−15)(35x+23)<0.
Lời giải
Ta có: (23x−15)(35x+23)<0
⇔[23(x−310)][35(x+109)]<0
⇔23.35(x−310)(x+910)<0
⇔(x−310)(x+109)<0
Từ đó suy ra: x−310 và x+109 trái dấu, mặt khác ta lại có x−310
Nên suy ra: x−310<0 và x+109>0⇔−109
Vậy các số hữu tỉ x thỏa mãn bài toán là −109
Bài tập tự luyện
Bài toán 1: Trong các câu sau, câu nào đúng, câu nào sai?
a) Số hữu tỉ dương lớn hơn số hữu tỉ âm
b) Số hữu tỉ dương lớn hơn số tự nhiên
c) Số 0 là số hữu tỉ âm
d) Số nguyên dương là số hữu tỉ.
Bài toán 6: Sắp xếp các số hữu tỉ sau theo thứ tự giảm dần:
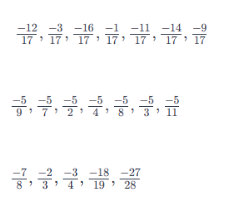
Bài toán 7: Cho số hữu tỉ 
với giá trị nào của a thì:
a) x là số nguyên dương;
b) x là số âm;
c) x không là số dương và cũng không là số âm.
Bài toán 8: Cho số hữu tỉ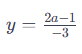 
Với giá trị nào của a thì:
a) y là số nguyên dương;
b) y là số âm;
c) y không là số dương và cũng không là số âm.
Bài toán 9: Cho số hữu tỉ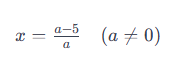 
. Với giá trị nào của a thì x là số nguyên.
Bài toán 10: Cho số hữu tỉ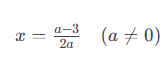 
. Với giá trị nào của a thì x là số nguyên.
Bài toán 11: Tìm các số nguyên dương n, biết:
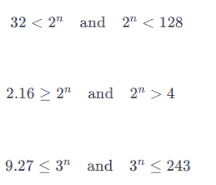
Bài toán 12: Chứng minh rằng với mọi số nguyên dương n, thì:
a)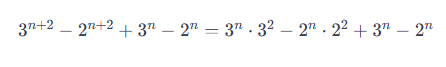 
chia hết cho 10
b) 
chia hết cho 6.
Bài toán 13: Tính
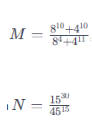
Bài 14
Trọng lượng của một vật thể trên Mặt Trăng bằng khoảng 1/6 trọng lượng của nó trên Trái Đất. Biết trọng lượng của một vật trên Trái Đất được tính theo công thức: P=10M với P là trọng lượng của vật tính theo đơn vị Niu-tơn (kí hiệu N; m là khối lượng của vật tính theo đơn vị ki-lô-gam.
(Nguồn: Khoa học tự nhiên 6, NXB Đại học Sư phạm, 2021)
Nếu trên Trái Đất một nhà du hành vũ trụ có khối lượng là 75.5 kg thì trọng lượng của người đó trên Mặt Trăng sẽ là bao nhiêu Niu-tơn (làm tròn kết quả đến hàng phần trăm)?
