Tìm tập xác định của hàm số là kiến thức cơ bản và cần phải nắm vững trong môn Toán Đại số lớp 10 THPT. Dưới đây là bài viết về chủ đề: Tập xác định của hàm số y = tan2x là gì?, là tài liệu tham khảo quan trọng cho các em học sinh cũng như thầy cô giáo.
Mục lục bài viết
1. Tập xác định của hàm số y = tan2x là gì?
Câu hỏi Tập xác định của hàm số y = tan2x là:
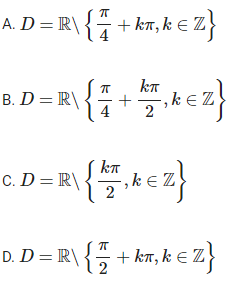
Giải chi tiết:
Điều kiện ![]()
Tập xác định: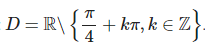
Chọn đáp án A
2. Tập xác định của hàm số là gì?
Tập xác định của một hàm số, được ký hiệu là D(f), là một tập con của tập số thực R, chứa tất cả các giá trị của biến độc lập mà khi thay vào hàm số, biểu thức đó vẫn xác định và không dẫn đến bất kỳ phép tính không hợp lệ nào. Trong bối cảnh này, việc hàm số “xác định” có nghĩa là mỗi giá trị trong tập xác định cho phép chúng ta tính toán một giá trị tương ứng của hàm số mà không gặp phải các vấn đề không thể giải quyết.
Ví dụ, xét hàm số f(x) = 1/(x-3). Để xác định tập xác định của hàm số này, ta cần loại bỏ những giá trị của biến mà dẫn đến việc chia cho 0, vì phép chia cho 0 là không xác định trong toán học. Do đó, ta không thể có x=3 trong tập xác định của hàm số này, vì khi thay x=3 vào biểu thức 1/(x−3), ta sẽ phải chia cho 0.
Tuy nhiên, với mọi giá trị x khác 3, biểu thức 1/(x−3) sẽ cho ra một kết quả xác định, nghĩa là nó thuộc vào tập xác định của hàm số. Chẳng hạn, khi x=5
x=5, ta có 1/ (5-3) = 1/2, và kết quả này là xác định.
Điều này cho thấy rằng tập xác định của hàm số f(x)= 1/(x-3) là tất cả các số thực x mà x≠3. Tức là ![]()
Các giá trị khác như 1, 2, 4,… đều thuộc vào tập xác định này.
Vì vậy, việc tìm tập xác định của một hàm số đồng nghĩa với việc xác định tất cả các giá trị của biến độc lập mà khi thay vào hàm số, ta vẫn có thể thực hiện các phép tính một cách hợp lệ và nhận được kết quả xác định.
Trong chương trình toán lớp 10, việc tìm tập xác định của các hàm số thường được phân loại theo các loại cơ bản dựa trên biểu thức của hàm số. Cụ thể, chúng ta có thể chia thành ba loại cơ bản như sau:
Loại 1: Hàm không chứa căn và không chứa mẫu
Trong loại này, các hàm số không chứa căn bậc 2 hoặc biểu thức dưới mẫu. Trong trường hợp này, tập xác định là toàn bộ tập số thực R.
Ví dụ:
Hàm số bậc nhất y=ax+b và
Hàm số bậc 2
y=ax^2+bx+c với a≠0
Loại 2: Hàm số chứa ẩn dưới mẫu
Trong trường hợp này, để hàm số xác định, mẫu của hàm số không thể bằng 0.
Ví dụ:
Tìm tập xác định của hàm số chứa mẫu:
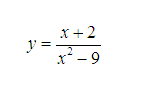
Lời giải:
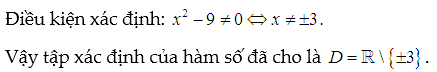
Loại 3: Hàm số chứa ẩn trong căn bậc chẵn
Trong trường hợp này, để hàm số xác định, biểu thức trong căn phải là số không âm (căn không dưới mẫu) hoặc nếu biểu thức trong căn là số âm, thì phải có mẫu dưới dạng căn để biểu thức trong căn không bị âm (căn dưới mẫu).
Ví dụ:
Tìm tập xác định của hàm số chứa căn:
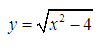
Lời giải:
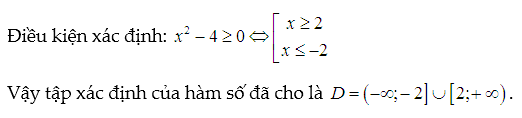
Chú ý:
Trong một số trường hợp, hàm số có thể chứa nhiều loại như đã nêu ở trên. Khi đó, để xác định tập xác định của hàm số, ta phải kiểm tra tất cả các điều kiện và có thể đặt chúng trong dấu hệ để đảm bảo rằng tất cả các điều kiện đều được thỏa mãn.
Ví dụ:
Tìm tập xác định của hàm số:
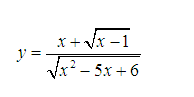
Lời giải:
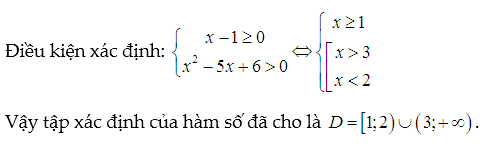
Đây là một phân tích chi tiết và phân loại cụ thể về cách xác định tập xác định của các loại hàm số thường gặp trong chương trình toán lớp 10. Điều này giúp học sinh hiểu rõ hơn về điều kiện để hàm số được xác định và áp dụng chúng trong việc giải các bài tập.
3. Tìm tập xác định hàm số bằng máy tính cầm tay:
Phương pháp sử dụng máy tính cầm tay để tìm tập xác định của hàm số là một công cụ hữu ích trong việc giải các bài toán trắc nghiệm. Không chỉ trả về kết quả chính xác mà còn giải quyết vấn đề một cách nhanh chóng và hiệu quả. Ý tưởng này khai thác chức năng của máy tính cầm tay, như CALC hoặc TABLE, để kiểm tra và xác định tập xác định của hàm số. Dưới đây là một ví dụ cụ thể để minh họa cách thức hoạt động của phương pháp này.
Khi bắt đầu, bạn mở máy tính cầm tay của mình và chuyển sang chế độ CALC bằng cách nhấn MODE 7. Tiếp theo, bạn nhập hàm số cần kiểm tra vào máy tính. Sau đó, bạn sẽ tiến hành kiểm tra từng đáp án để xác định tập xác định của hàm số.
Ví dụ, nếu có các đáp án A, B, C, D, bạn sẽ bắt đầu kiểm tra từng đáp án một. Đối với đáp án A, bạn sẽ thiết lập giới hạn của biến độc lập trong khoảng mà đáp án đó đề cập. Chẳng hạn, nếu đáp án A nằm trong khoảng từ 2 đến 4, bạn sẽ đặt giới hạn bắt đầu là 2 và kết thúc là 4 trên máy tính. Sau đó, bạn sẽ thiết lập bước nhảy để kiểm tra các giá trị trên khoảng đó. Ví dụ, nếu bạn chọn 20 điểm trên khoảng từ 2 đến 4, bạn sẽ đặt bước nhảy là
(4−2)/20.
Sau khi thiết lập các thông số này, máy tính sẽ tính toán và hiển thị giá trị của hàm số tại mỗi điểm trong khoảng đã chọn. Nếu có bất kỳ giá trị nào trong khoảng đó tạo ra lỗi (ERROR) hoặc không xác định, bạn sẽ loại bỏ đáp án đó khỏi danh sách.
Tiếp tục quá trình kiểm tra này cho đến khi bạn tìm ra đáp án đúng – đó là đáp án mà tất cả các giá trị trong khoảng đã chọn không tạo ra lỗi khi được thay vào hàm số.
Phương pháp này cho phép bạn kiểm tra và xác định tập xác định của hàm số một cách nhanh chóng và dễ dàng, giúp bạn giải quyết các bài toán trắc nghiệm một cách hiệu quả.
4. Bài tập về tập xác định của hàm số:
Bài tập số 1. Cho các hàm số sau, hãy tìm TXĐ của chúng:
a, f(x)=x-3
b, g(x)=x+3×2-4
c, h(x)=2x-1-3x-2
Hướng dẫn
a, Hàm số đã cho xác định khi và chỉ khi: x−3 ⩾ 0 ⇔ x ⩾ 3.
Kết luận: TXĐ D= [3,+∞).
b, Hàm số đã cho xác định khi và chỉ khi: x2−4 ≠ 0 ⇔ x ≠ ±2.
Kết luận: TXĐ D = R∖{±2}.
c, Hàm số đã cho xác định khi và chỉ khi: x−1 ⩾ 0; |x|−2 ≠ 0 ⇔ x ⩾ 1 và x ≠ ±2 ⇔ x ⩾ 1 và x ≠ 2.
Kết luận: TXĐ D = [1,2)∪(2,+∞).
Bài tập số 2. Cho các hàm số sau, hãy tìm TXĐ của chúng:
f(x)=2x-3+x+23-x
Hướng dẫn
Hàm số đã cho xác định khi và chỉ khi: 2x−3 ⩾ 0 và 3−x > 0 ⇔ x ⩾ 32 và x < 3.
Kết luận: TXĐ D= [32,3).
Bài tập số 3. Cho các hàm số sau, hãy tìm TXĐ của chúng:
f(x)=x2-2x+3+1x+1
Hướng dẫn
Hàm số đã cho xác định khi và chỉ khi: x2−2x+3 ⩾ 0 và |x|+1 ≠ 0 ⇔ (x-1)2+2 ⩾ 0 và |x|+1 ≠ 0.
Các điều kiện này đều luôn luôn đúng với mọi số thực x do đó, tập xác định của hàm số là D=R.
Bài tập số 4. Tìm m để hàm số f(x)=2xx-m+1 xác định trên (0,2).
Hướng dẫn
Hàm số đã cho xác định khi và chỉ khi: x≠m−1.
Do đó, muốn hàm số xác định trên (0,2) thì m−1 không được nằm trong khoảng (0,2). Tức là: m−1 ⩽ 0 hoặc m−1 ⩾ 2.
Từ đó tìm được đáp số m ⩽ 1 hoặc m ⩾ 3.
Bài tập số 5. Tìm m để hàm số f(x)=x-m+1+2x-m xác định với mọi x > 0.
Hướng dẫn
Hàm số đã cho xác định khi và chỉ khi x−m+1 ⩾ 0 và 2x−m ⩾ 0 ⇔ x ⩾ m−1 và x ⩾ m2.
Do đó, muốn hàm số xác định với mọi x > 0 thì m−1 ⩽ 0 và m2 ⩽ 0.
Từ đó tìm được đáp số m ⩽ 0.
THAM KHẢO THÊM:




