Tích phân là một công cụ quan trọng trong toán học và có nhiều ứng dụng rộng rãi trong các lĩnh vực khác nhau. Một trong những ứng dụng quan trọng của tích phân là tính toán thể tích khối tròn xoay. Để nắm chắc kiến thức, mời các bạn tham khảo bài viết Ứng dụng tích phân tính thể tích khối tròn xoay và cách giải dưới đây.
Mục lục bài viết
1. Ứng dụng tích phân tính thể tích khối tròn xoay:
Tích phân là một công cụ quan trọng trong toán học và có nhiều ứng dụng rộng rãi trong các lĩnh vực khác nhau. Một trong những ứng dụng quan trọng của tích phân là tính toán thể tích khối tròn xoay. Thể tích khối tròn xoay là một khái niệm cơ bản trong hình học và được áp dụng trong nhiều lĩnh vực khác nhau như vật lý, kỹ thuật và thiết kế.
– Trong vật lý, tính toán thể tích khối tròn xoay là một phần quan trọng của việc xác định đặc tính và tính chất của các vật thể quay. Ví dụ, khi nghiên cứu về động học chất lỏng, tính toán thể tích của một bể chứa chất lỏng có hình dạng khối tròn xoay giúp chúng ta hiểu được lượng chất lỏng tối đa mà bể có thể chứa và quá trình tràn đổ khi vượt quá giới hạn đó. Ngoài ra, trong nghiên cứu về động lực học cơ học, tính toán thể tích khối tròn xoay của các vật thể quay, như đĩa máy, trục động cơ và cánh quạt, giúp xác định khối lượng và động lượng của chúng, từ đó phân tích hiệu suất và tính toán các thông số quan trọng.
– Trong kỹ thuật, tính toán thể tích khối tròn xoay được áp dụng rộng rãi trong thiết kế và sản xuất các chi tiết và linh kiện có hình dạng tròn xoay. Ví dụ, trong công nghệ ô tô, tính toán thể tích của các bình chứa nhiên liệu, hệ thống làm mát và các bộ phận khác có hình dạng tròn xoay giúp xác định dung tích và hiệu suất của chúng. Trong công nghệ xây dựng, tính toán thể tích của các cột thép, cột nước và các vật liệu xây dựng có hình dạng tròn xoay giúp ước lượng lượng vật liệu cần thiết và tính toán các thông số kỹ thuật.
– Ngoài ra, tính toán thể tích khối tròn xoay cũng được áp dụng trong các lĩnh vực như thiết kế đồ họa và nghệ thuật. Trong thiết kế đồ họa, tính toán thể tích của các hình dạng quay giúp xây dựng mô hình 3D và tạo ra các hiệu ứng đặc biệt trong các phần mềm thiết kế. Trong nghệ thuật, tính toán thể tích của các tác phẩm điêu khắc và hình dạng nghệ thuật khác có hình dạng tròn xoay giúp nghệ sĩ hiểu và sử dụng không gian một cách sáng tạo.
Tổng quát, ứng dụng của tích phân trong việc tính toán thể tích khối tròn xoay rất đa dạng và quan trọng trong nhiều lĩnh vực. Nó cho phép chúng ta hiểu và phân tích các đặc tính và tính chất không gian của các hình dạng tròn xoay, từ đó áp dụng vào thiết kế, nghiên cứu và giải quyết các vấn đề thực tế. Tích phân và tính toán thể tích khối tròn xoay cung cấp cho chúng ta một phương pháp chính xác và linh hoạt để nắm bắt và ứng dụng các khái niệm không gian trong thế giới xung quanh chúng ta.
2. Cách giải tích phân tính thể tích khối tròn xoay:
Để tính thể tích của vật thể H, ta sử dụng công thức tích phân:
![]()
Trong đó, S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x.
Để tính toán, ta cần biết hàm S(x), tức là diện tích thiết diện tại mỗi điểm x.
Nếu bạn cung cấp hàm S(x) cụ thể, tôi có thể giúp bạn tính toán thể tích V bằng cách thay thế hàm S(x) vào công thức tích phân và tính giá trị của nó từ a đến b.
Công thức tính thể tích vật thể tròn xoay khi quay miền D được giới hạn bởi các đường y = f(x), y = 0, x = a, x = b quanh trục Ox là:
![]()
Trong đó:
V là thể tích vật thể tròn xoay.
π là số pi, có giá trị xấp xỉ 3.14159.
Phép tích phân từ a đến b của hàm f^2(x), tức là tích phân của bình phương của hàm f(x) trên khoảng từ a đến b.
Lưu ý: Công thức này chỉ áp dụng khi miền D được giới hạn bởi đường y = f(x), đường y = 0, và đường x = a, x = b.
2. Bài tập vận dụng:
Câu 1: Thể tích của khối tròn xoay tạo nên khi quay quanh trục Ox hình phẳng giới hạn bởi (C): y = lnx, trục Ox và đường thẳng x = e là:
A. V=π(e+1).
B. V=π(e−1).
C. V=πe.
D. V=π(e−2).
Câu 2: Tính thể tích V của khối tròn xoay khi quay hình phẳng (H) giới hạn bởi đồ thị hàm số
y=4−x, đường thẳng x =2 và trục Ox quanh trục Ox
A. 3π3
B. 2π2
C. π
D. 4π
Câu 3: Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y=x12.ex2,x=1,x=2,y=0 Y=x12.ex2 , x=1 , x=2 , y=0 quanh trục Ox là:
A. πe^2
B. πe
C. π(e^2−e)
D. π(e^2+e)
Câu 4: Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y=√x,y=0,x=4, quay quanh trục Ox. Đường thẳng x = a (0 < a < 4) cắt đồ thị hàm số y=√x tại M (hình vẽ bên). Gọi V1 là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng V = 2V1. Giá trị của a thỏa mãn là?
A [1; 2).
B. [2; 3).
C. [3; 4).
D. (0; 1).
Câu 5: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số y = f(x) trục Ox và hai đường thẳng x = a, x = b (a < b) xung quanh trục Ox.
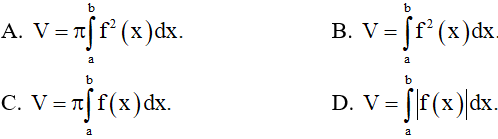
Câu 6: Viết công thức tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm x = a, x = b (a < b), có thiết diện bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (a ≤ x ≤ b) là S(x).

Câu 7: Hình phẳng C giới hạn bởi các đường y = x2 + 1 , trục tung và tiếp tuyến của đồ thị hàm số y = x2 + 1 tại điểm (1; 2), khi quay quanh trục Ox tạo thành khối tròn xoay có thể tích bằng:
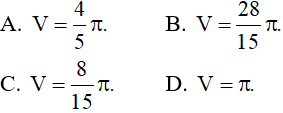
Câu 8: Cho hình phẳng D giới hạn bởi đường cong y = ex, trục hoành và các đường thẳng x = 0; x = 1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ?
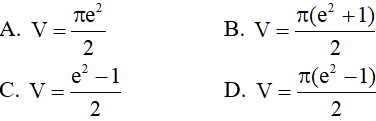
Câu 9: Hình phẳng giới hạn bởi đồ thị hai hàm số y = 2x – x2 và y = x khi quay quanh trục Ox tạo thành khối tròn xoay có thể tích bằng:
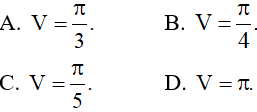
Câu 10: Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bởi các parabol y = 4 – x2 và y = 2 + x2 quay quanh trục Ox là kết quả nào sau đây?
A. V = 10π
B. V = 12π
C. V= 14π
D. V = 16π
Câu 11: Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường 4y = x2 ,y = x qua quanh trục hoành bằng bao nhiêu?
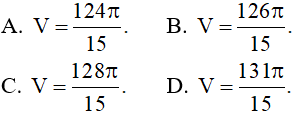
Câu 12: Thể tích của khối tròn xoay tạo nên khi quay quanh trục Ox hình phẳng giới hạn bởi (C): y = lnx, trục Ox và đường thẳng x = e là:
A. V = π(e – 2)
B. V = π(e – 1)
C. V = πe
D. V = π(e + 1)
Câu 13: Tính thể tích V của khối tròn xoay khi quay hình phẳng (H) giới hạn bởi đồ thị hàm số y = x4 – 1 và trục Ox quanh trục Ox.

Câu 14: Tính thể tích V của khối tròn xoay khi quay hình phẳng (H) giới hạn bởi đồ thị hàm số y = x2 + 1, đường thẳng x = 0, đường thẳng x = 3 và trục Ox quanh trục Ox.
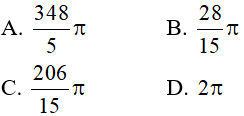
Câu 15: Tính thể tích V của khối tròn xoay khi quay hình phẳng (H) giới hạn bởi đồ thị hàm số y = x3 + 2,đường thẳng x = -1, đường thẳng x = 1 và trục Ox quanh trục Ox.

Câu 16: Tính thể tích V của khối tròn xoay khi quay hình phẳng (H) giới hạn bởi đồ thị hàm số y = (x + 1)2, trục hoành và trục tung quanh trục Ox.

Câu 17: Tính thể tích khối tròn xoay khi quay hình phẳng (H) giới hạn bởi (C):y = -x2 + 2x và trục Ox quanh trục Ox.
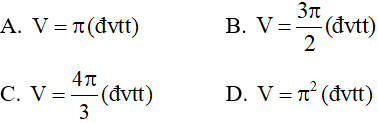
Câu 18: Thể tích của khối tròn xoay tạo nên do quay quanh trục hình phẳng giới hạn bởi các đường y = (1 – x2), y = 0,x = 0 và x = 2 bằng:
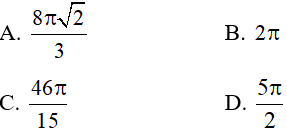
Câu 19: Cho (H) là hình phẳng giới hạn bởi (P)y = x2 – 4x + 4, y = 0, x = 0, x = 3 .Thể tích V khi quay (H) quanh trục Ox là:

Câu 20: Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường ![]() quanh trục Ox là:
quanh trục Ox là:
A. π(e2 + e)
B. π(e2 – e)
C. πe2
D. πe
Câu 21: Cho hình chữ nhật ABCD có AB = 4, AD = 8 (như hình vẽ).
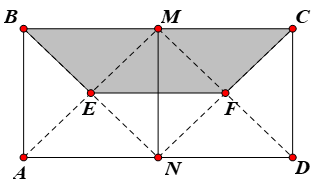
Gọi M, N , E, F lần lượt là trung điểm của BC, AD, BN và NC. Tính thể tích V của vật thể tròn xoay khi quay hình tứ giác BEFC quanh trục AB.
A. 100π. B. 96π.
C. 84π. D. 90π
Câu 22: Thể tích của khối tròn xoay do hình phẳng (H) giới hạn bởi các đường y = sinx; y = 0; x = 0; x = π khi quay xung quanh Ox là:





