Tập xác định của hàm số là một bước nhỏ những rất quan trọng trong các bài tập liên quan đến hàm số mũ và logarit. Nắm chắc cách làm bài tập về tập xác định của hàm số giúp các bạn làm các dạng bài về hạm số mũ và logarit đơn giản hơn và nhanh chóng. Để hiểu rõ, mời các bạn tham khảo bài viết Tập xác định của hàm số y = log2(x-1) là gì? dưới đây.
Mục lục bài viết
1. Tập xác định của hàm số y = log2(x-1) là gì?
Câu hỏi: Tập xác định của hàm số y = log2(x – 1) là:
A. [1; +∞);
B. [1; +∞) {2};
C. (1; +∞);
D. (0; +∞).
Lời giải:
Đáp án đúng là: C
Điều kiện: x – 1 > 0 hay x > 1.
Suy ra tập xác định của hàm số log2(x – 1) là (1; +∞).
2. Phương pháp tìm tập xác định của hàm số:
Trước hết các em cần phải hiểu thật chính xác tìm tập xác định của hàm số là gì? Tìm tập xác định có nghĩa là ta phải xét các điều kiện làm sao cho hàm số có nghĩa.
– Hàm số có chữa mẫu thì điều kiện để hàm số có nghĩa là mẫu phải ≠ 0.
– Hàm số có chứa căn thức thì biểu thức trong căn phải ≥ 0 để hàm số có nghĩa.
– Hàm số logarit có nghĩa khi biểu thức của loga ≥ 0
– Hàm số lũy thừa chia thành 3 trường hợp:
Nếu hàm số có mũ nguyên dương thì cơ số ∈ R
Mũ nguyên âm hoặc mũ = 0 thì cơ số phải ≠ 0
Mũ không nguyên thì cơ số phải > 0
Những kiến thức trên đây là kiến thức bắt buộc mà học sinh lớp 12 phải nhớ nếu muốn làm được dạng bài tập này. Bây giờ chúng ta sẽ lần lượt đi tìm phương pháp giải cho các dạng hàm số nhé.
Cách giải phương trình Logarit bằng máy tính
– Giải phương trình trắc nghiệm
Bước 1: Chuyển phương trình về 1 vế > Nhập phương trình vào trong máy tính.
Bước 2: Bấm CALC thử lần lượt các đáp án A, B, C, D vào phương trình > Bấm “=” > Nếu kết quả bằng 0 thì đáp án đó là đáp án đúng.
– Giải phương trình Logarit bằng tính năng SOLVE
Tính năng SOLVE trên máy tính cầm tay là tính năng cho phép giải nhanh để tìm nghiệm X bất kỳ, phù hợp với một số bài toán trắc nghiệm, cần giải nhanh. Tuy nhiên tính năng này không làm tròn được một số giá trị phức tạp, cũng như không rà được toàn bộ nghiệm phương trình.
Bước 1: Chuyển phương trình về 1 vế và nhập trực tiếp phương trình vào máy tính cầm tay.
Bước 2: Ấn SHIFT + CALC.
– Giải phương trình Logarit bằng tính năng TABLE
Bước 1: Bấm MODE > 7 > Nhập hàm số: f(x) = Log3(3X) Log3(9X) – 4.
Bước 2: Nhấn “=” > Chọn START = 0 > “=” > Chọn END = 29 > “=” > Chọn STEP = 1 > “=”.
Bước 3: Dò cột f(x) để tìm những khoảng hàm số đổi dấu. Ví dụ như hình dưới đây ta thấy khoảng (0;1) và (1;2) hàm số đổi dấu từ âm sang dương. Vậy trên khoảng này sẽ có khả năng có nghiệm, ta sẽ xét tiếp 2 khoảng này.
Dò khoảng nghiệm của phương trình
Bước 4: Bấm AC và dấu = để làm lại các bước trên. Với khoảng (0;1) ta chọn START = 0 > END = 1 > STEP 1/29. Ta được khoảng (0;0,0344) có thể có nghiệm, ta sẽ dò tiếp khoảng này để tìm nghiệm gần đúng nhất.
Dò tiếp khoảng nghiệm nhỏ hơn
Bước 5: Với khoảng (0;0,0344) ta chọn START = 0 > END = 1 > STEP = 0,0344/29. Ta được nghiệm nằm trong khoảng (0,0189-0,0201).
Ra khoảng nghiệm gần đúng thứ 2
Bước 6: Muốn có nghiệm chính xác hơn nữa ta lặp lại với START = 0,0189 > END = 0,0201 > STEP = (0,0201-0,0189)/29. Ta được nghiệm đúng thứ nhất là 0,01997586207.
Tìm ra nghiệm thứ nhất của bài toán
Bước 7: Làm tương tự với khoảng (1;2). Ta được nghiệm đúng thứ hai là 1,852482759.
Tìm ra nghiệm thứ hai của bài toán
Bước 8: Bấm tích hai nghiệm với nhau ta thu được kết quả của bài toán.
3. Bài tập vận dụng có đáp án:
Bài 1: Tìm tập xác định D của hàm số
![]()
Lời giải:
Hàm số xác định khi và chỉ khi 1-x2 ≠ 0 ⇔ x ≠ ±1
Bài 2: Tìm tập xác định D của hàm số
![]()
Lời giải: Hàm số xác định khi và chỉ khi 1-2x > 0 ⇔ x < 1/2
Bài 3: Tìm tập xác định D của hàm số
y = (2x – 4) -2018
Lời giải: Hàm số xác định khi và chỉ khi 2x-4 ≠ 0 ⇔ x ≠ 2
Bài 4: Tìm tập xác định D của hàm số
y = (4 – x) 3/11
Lời giải: Hàm số xác định khi và chỉ khi 4-x > 0 ⇔ x < 4
Bài 5: Tìm tập xác định D của hàm số
![]()
Lời giải: Hàm số xác định khi và chỉ khi 1+x-2x2 > 0 ⇔ -1/2 < x < 1
Bài 6: Tìm tập xác định D của hàm số
![]()
Lời giải: Hàm số xác định khi và chỉ khi
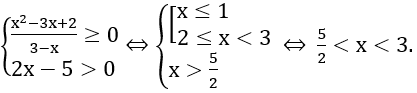
Vậy tập xác định của hàm số là D= (5/2; 3).
Bài 7: Tìm tập xác định D của hàm số
![]()
Lời giải: Hàm số xác định khi và chỉ khi
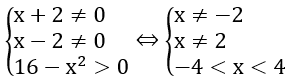
Vậy tập xác định của hàm số là D=(-4 ; 4){-2 ,2}.
Bài 8: Tìm tập xác định của hàm số
y = log2 (5x + 2) – 125)
Lời giải: Hàm số xác định khi 5x+2-125 > 0 ⇔ 5x+2 > 53 ⇔ x > 1.
Vậy tập xác định D=(1;+∞).
Lời giải: Để hàm số y=log(x2-2x-m+1) có tập xác định là R
Bài 9: Tìm mệnh đề đúng trong các mệnh đề sau:
A. Đồ thị hàm số y = ax và đồ thị hàm số y = logax đối xứng nhau qua đường thẳng y = x.
B. Hàm số y = ax với 0 < a < 1 đồng biến trên khoảng (-∞; +∞).
C. Hàm số y = axvới a > 1 nghịch biến trên khoảng (-∞; +∞)
D. Đồ thị hàm số y = ax với a > 0 và a ≠ 1 luôn đi qua điểm M (a;1).
Lời giải:
Đáp án: A
Giải thích:
Chọn A
Câu B sai vì hàm số y = ax với 0 < a < 1 nghịch biến trên khoảng (-∞; +∞).
Câu C sai vì hàm số y = ax với a > 1 đồng biến trên khoảng (-∞; +∞).
Câu D sai vì đồ thị hàm số y = ax với a < 0 và a ≠ 1 luôn đi qua điểm M(a; aa) hoặc M(0;1) chứ không phải M(a;1).
Bài 10: Với a > 0 và a ≠ 1. Phát biểu nào sau đây không đúng?
A. Hai hàm số y = ax và y = logax có cùng tính đơn điệu
B. Hai hàm số y = ax và y = logax có cùng tập giá trị
C. Đồ thị hai hàm số y = ax và y = logax đối xứng nhau qua đường thẳng y=x.
D. Đồ thị hai hàm số y = ax và y = logax đều có đường tiệm cận
Lời giải:
Đáp án: B
Giải thích:
Tập giá trị của hàm số y = ax là (0; +∞), tập giá trị của hàm số y = logax là R.
Bài 11: Cho hàm số y=(√2-1)x. Phát biểu nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng (-∞; +∞).
B. Hàm số đồng biến trên khoảng (0; +∞)
C. Đồ thị hàm số có đường tiệm cận ngang là trục tung.
D. Đồ thị hàm số có đường tiệm cận đứng là trục hoành
Lời giải:
Đáp án: A
Giải thích:
Vì 0 < √2-1 < 1 nên hàm số y = (√2-1)x nghịch biến trên khoảng (-∞; +∞)
Bài 12: Tìm giá trị lớn nhất của hàm số f(x)=x2 e2 trên đoạn [-1;1]
A. 2e
B. 1/e
C. e
D. 0
Lời giải:
Đáp án: C
Giải thích:
Trên đoạn [-1;1], ta có: f’ (x)=xex (x+2); f’ (x)=0 ⇔ x = 0 hoặc x = -2 (loại).
Bài 13: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=2|x| trên [-2;2]
A. maxy=4; miny=-1/4
B. maxy=4; miny=1/4
C. maxy=1; miny=1/4
D. maxy=4; miny=1
Lời giải:
Đáp án: D
Giải thích : Đặt t = |x|, với x ∈ [-2;2] ⇒ t ∈ [0;2]
Xét hàm f(t) = 2t trên đoạn [0;2]; f(t) đồng biến trên [0;2]
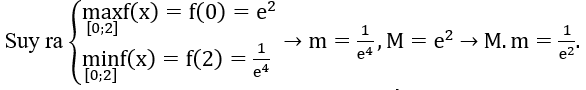
Hoặc với x ∈ [-2;2] ⇒ |x| ∈ [0;2]. Từ đây, suy ra: 20 ≤ 2|x| ≤ 22 ⇔ 1 ≤ 2|x| ≤ 4
Bài 14: Gọi m và M lần lượt là giá trị nhỏ nhất và lớn nhất của hàm số f(x)=e2-3x trên đoạn [0;2]. Mệnh đề nào sau đây là đúng?
A. m+M = 1
B. M-m = e.
C. M.m = 1/e2
D. M/m = e2
Lời giải:
Đáp án: C
Giải thích:
Hàm số f(x) xác định và liên tục trên đoạn [0;2].
Đạo hàm f'(x) = -3e2-3x < 0, ∀x ∈ R. Do đó hàm số f(x) nghịch biến trên [0;2].
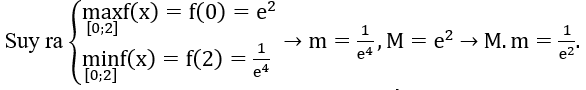
Bài 15: Chọn khẳng định đúng khi nói về hàm số y=(lnx)/x
A. Hàm số không có cực trị.
B. Hàm số có một điểm cực đại
C. Hàm số có một điểm cực tiểu
D. Hàm số có một điểm cực đại và một điểm cực tiểu
Lời giải:
Đáp án: C
Giải thích:
Hàm y’ đổi dấu từ âm sang dương khi qua x=e nên x=e là điểm cực tiểu của hàm số.
THAM KHẢO THÊM:




