Tính nhanh nguyên hàm tích phân bằng máy tính Casio

Bước 1 Nhập tích phân

Bước 2 Nhấn phím =

Vậy phương án D là đáp án

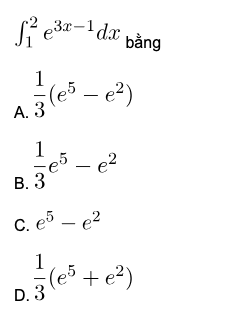
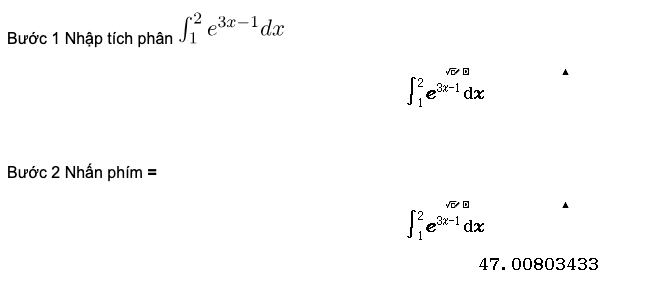
Bước 3 Chuyển các giá trị ở bốn phương án sang dạng hiển thị thập phân

 

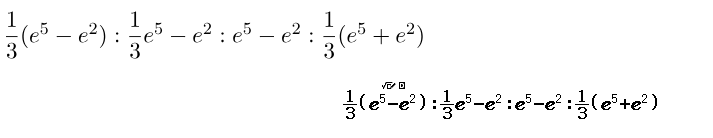
Bước 4 Nhấn phím =

Vậy phương án A là đáp án

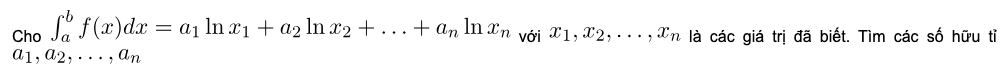
Bước 1 Biến đổi sơ cấp

Bước 2 Chọn phương thức tính toán Table

Bước 3 Nhập tích phân

Bước 4 Nhập  Start=1, End=45, Step=1 

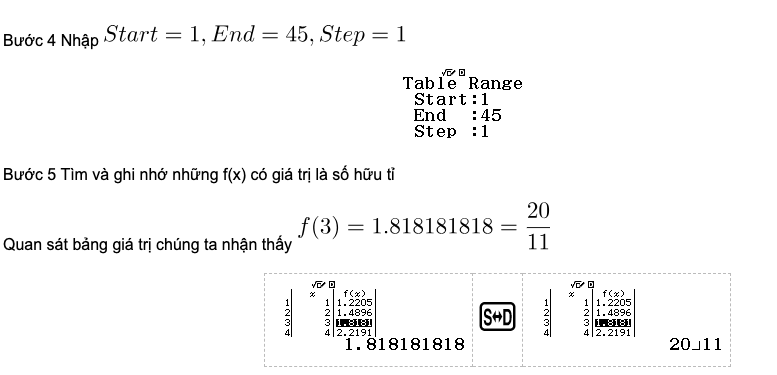
Bước 5 Tìm và ghi nhớ những f(x) có giá trị là số hữu tỉ

Bước 6 Chọn phương thức tính toán Calculate

Bước 7 Sử dụng tính năng FACT phân tích tử số và mẫu số thành thừa số nguyên tố

Bước 8 Biến đổi sơ cấp rồi suy ra các giá trị a1,a2,….,an

Bước 1 Biến đổi sơ cấp

Bước 2 Chọn phương thức tính toán Table

Bước 3 Nhập tích phân

 

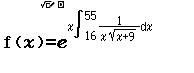
Bước 6 Chọn phương thức tính toán Calculate

Bước 7 Sử dụng tính năng FACT phân tích tử số và mẫu số thành thừa số nguyên tố

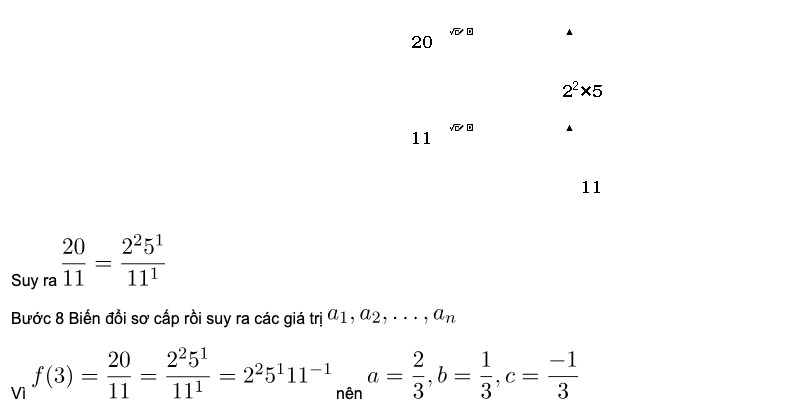
Vậy phương án A là đáp án

4. Một số dạng bài tập vận dụng các tính nhanh nguyên hàm tích phân bằng máy tính Casio: 

Dạng ∫ P(x)/Q(x) trong đó bậc của p(x) >= Q (x). Ta thực hiện phép chia đa thức. Áp dụng phương pháp CALC 100

Ta giả sử Q(x) = (x – x1)(x – x2)(x – x3) (nhiều hay ít hơn cũng làm tương tự):

)(x) / Q(x) = A /(x- x1) + B / (x – x2) + C/ (x – x3) + R(x) là biểu thức dư của phép chia

Tím A = d/dx (P(x) / (x – x2)(x – x3) | x = x1

B = d/dx P(x) / (x – x1)( x- x3) | x = x2

C = d/dx P(x) / (x – x1)(x – x2) | x = x3

Tìm R(x) = d/dx (P(x)/(x – x1)(x – x2)(x – x3) – A/(x – x1) – B/(x – x2) – C/(x – x3)) | x = 100 sử dụng cachs tách 100

Dạng f(x) = (ax + b)/(x – x1)(x – x2) cần tách đưa về dạng A/(x – x1) + B/(x – x2)

Cách 1. Bấm: (aX + b) /( d/dx (X – x1)(X – x2))|x = X

CALC X = x1 -> A

CALC X = x2 -> B

Cách 2. Bấm: (aX + b) /(X – x1)(X – x2) x (X – x1)

CALC X = x1 + 0,0000001 -> A

CALC X = x2 + 0,0000001 -> B

Tách phân thức (ax + b)/(cx + d) = a/c + K/(cx + d)

Nhập máy tính: (aX + b / cX + d – a/c)(cX + d) CALC X = 10

Khi đó: ∫ ax + b / cx + d dx = ∫ ( a/c + K/ cx + d)dx = ax/c + Kc Ln |cx + d|

Bài tập 1: Tìm 1 nguyên hàm F(x) của hàm số f(x), biết F(x0) = M

Cú pháp: F1(A) – M – ∫(x0->A)f(x) dx

Ví dụ: Tìm nguyên hàm F(x) của hàm số f(x) = (x3 +  3×2 + 3x -1) / (x2 + 2x + 1), biết F(1) = 1/3

A. F(x) = x2/2 + x + 2/x+1 – 6/13

B. F(x) = x2/2 + x + 2/(x+1)

C. F(x) = x2/2 + x + 2/x+1 + 13/6

D. F(x) = x2/2 + x + 2/x+1 – 13/6

A2/2 + A + 2/A+1 – 6/13 – ∫(1-> A) (x3 + 3×2 + 3x -1)/(x2 + 2x + 1) gán A = 0,1; 1 đều nhận kết quả khác 0 => loại đáp án A

A2/2 + A + 2/(A+1) – 13/6 – ∫(1-> A) (x3 + 3×2 + 3x – 1)/(x2 + 2x + 1) gán A = 0,1; 1 nhận kết quả 0, kiểm tra thêm => chọn D

Bài tập 2: Tính tích phân ∫(a->b) f(x)dx (Trong các đáp án đều là số vô tỷ, dạng căn, số e, số pi các bạn nên bấm máy ghi nhận lại các kết quả trên)

Cú pháp:

Ví dụ:  bằng

A. (e2 + 1)/4

B. (2e3 + 1)/9

C. (3e3 + 2)/8

D. (2e2 + 3)/3

(e2 + 1)/4 xấp xỉ 2,097264025

(2e3 + 1)/9 xấp xỉ 4,574563716

(3e3 + 2)/8 xấp xỉ 7,782076346

(2e3 + 3)/3 xấp xỉ 5,926037399

Bài tập 3: Diện tích hình phẳng – Thể tích khối tròn xoay

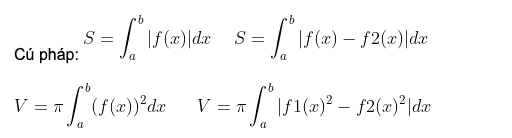
Ví dụ: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x2 – 2x , y = x là

A. 9/4

B. 9/2

C. 13/4

D. 7/4

Phương trình hoành độ giao điểm f1(x) – f2(x) = 0 <=> x2 – 3x = 0 <=> x = 0; x = 3

S = ∫(0->1)|x (e^x – e)|dx = e/2 – 1 = 0,35140914

Ví dụ: Hình (H) giới hạn bởi các đường thẳng y = x2 – 2x; y = 0; x = -1; x = 2. Tính thể tích của vật thể tròn xoay khi (H) xoay quanh trục Ox

A. 18 pi/5      B. 17 pi/5

C. 5 pi/18     D. 16 pi/5

V = pi x ∫(-1->2)(x2 – 2x)^2 dx = 18 pi/5

Bài tập 4:  Cho hàm số y = f(x) thỏa mãn f'(x) = (x + 1) e^x và ∫ f(x)dx = (ax + b). e^x + C với a, b thuộc R. Tính a + b

A. 0

B. 3

C. 2

D. 1

Ta có F(x) = (ax + b)e^x + C là nguyên hàm của f(x) và f'(x) =(x + 1).e^x

Đặt F”(x) = f'(x)

∫ f'(x)dx = ∫(x + 1)e^xdx = x.e^x + C = f(x)

∫f(x)dx = ∫x.e^x dx = (x -1).e^x + C

Vậy a = 1, b = -1 => a + b = 0

Bài tập 5: Gọi F(x) là một nguyên hàm của hàm số f(x) = 2^x, thỏa mãn F(x) = 1/Ln2. Tính giá trị của biểu thức T = F(0) + F(1) + F(2) + …. + F(2017)

A. T = 1009. (2^2017 + 1)/In2

 B. T = 2 ^2017.2018

C. T = (2^2017 – 1) / In 2

D.T = (2^2018 -1)/In 2

Ta có: F(x) = ∫2^xdx = 2^x / In2

T = F(0) + F(1) + F(2) + … + F(2017) = 2^0/In2 + 2/In2 + 2^1/In2 +…. + 2^2017/In2 = 1/In2. 91 – 2^2018)/-1 = (2^2018 -1)/In2

Bấm máy: ta cũng biến đổi để ra được F(x) = 2^x/In2

Bấm SHIFT Log

Bấm gán vào A, lấy A trừ đi đáp án đã rút gọn. Chọn D

Bài tập 6: Tìm nguyên hàm F(x) của hàm số f(x)

Cú pháp: f(A) – d/dx(Fi(x))|x = A

Trong đó: f(A): giá trị của f(x) tại x = A (A là hằng số bất kỳ thuộc tập xác định và A lấy giá trị bé 0,1;0,2;0,3…1,;1,1

F(x): các kết quả nguyên hàm

Ví dụ: 

 

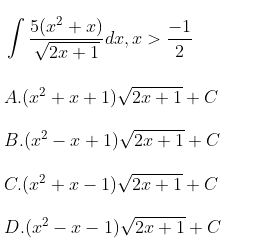
Bước 1: Nhập 5(A² + A) /(căn 2A + 1) – d/dx(x² + x + 1) căn(2x+1) | x = A (RCL – A; Shift )

Bước 2: Gán x = A = 1 hoặc 0,1 (bấm CALC -> A) cho kết quả khác 0 ta loại ngay đáp án đó => Loại A

Thay F1(x) bởi đáp án B và gán A như trên ta nhận kết quả khác 0 => Loại B

Thay F1(x) bởi đáp án C và gán A như trên ta nhận kết quả bằng 0; chắc ăn kiểm tra thêm vài giá trị của A như 0; 0,2; 0,5, 1

=> Chọn C (Không nên gắn x = A giá trị quá lớn máy sẽ lag)