Bộ giải toán Tập nghiệm của bất phương trình đã được biên soạn và đăng tải trên Luật Dương Gia. Sau đây là các dạng bài tìm Tập nghiệm của bất phương trình kèm bài tập có đáp án. Xin mời các em học sinh cùng đón xem.
Mục lục bài viết
1. Bất phương trình tuyến tính:
Bất phương trình tuyến tính là sự so sánh hai biểu thức bằng cách sử dụng các ký hiệu như < (nhỏ hơn), > (lớn hơn), ≤ (nhỏ hơn hoặc bằng), ≥ (lớn hơn hoặc bằng) và ≠ (không bằng).
* Ví dụ :
Tìm tập nghiệm của bất phương trình 7 – 2x < 3
Lời giải:
7 – 2x < 3
⇒ -2x < -4
⇒ x > 2
⇒ x ∈ (-∞,2)
Lưu ý: Khi chia cả hai vế của bất đẳng thức cho -2, ta phải đổi chiều của bất phương trình. Có thể tham khảo đồ thị của các hàm ở hai bên của bất phương trình.
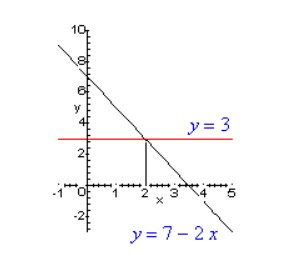
Để thỏa mãn bất phương trình, 7 – 2x cần phải nhỏ hơn 3. Vậy ta đang tìm số x sao cho điểm trên đồ thị y = 7 – 2x nằm dưới điểm trên đồ thị y = 3. Điều này đúng với x > 2. Trong ký hiệu khoảng, tập nghiệm là (-∞,2).
* Bài tập:
Bài 1: Tìm tập nghiệm của bất phương trình 4 – x > 1 + 3x
Lời giải:
4 – x > 1 + 3x
⇒ -4x > -3
⇒ x < ¾
⇒ x ∈ (-∞,¾)
Giải thích chi tiết:
Để giải bất phương trình 4 – x > 1 + 3x, ta làm như sau:
Trước hết, ta chuyển các số hạng có chứa x về một phía và các số hạng không chứa x về phía còn lại:
– x – 3x > 1 – 4
Tiếp theo, ta gộp các số hạng có chứa x và không chứa x:
-4x > -3
Sau đó, ta chia cả hai vế cho -4 (lưu ý rằng khi nhân hoặc chia cả hai vế của bất phương trình cho một số âm thì dấu của bất phương trình sẽ đổi chiều):
x < ¾
Vậy tập nghiệm của bất phương trình là x ∈ (-∞,¾)
Bài 2: Tìm tập nghiệm của bất phương trình x + 3 <= 10
Lời giải:
x + 3 ≤ 10
⇒ x ≤ 7
⇒ x ∈ (-∞,7]
Giải thích chi tiết:
Để giải bất phương trình x + 3 ≤ 10 một cách chi tiết hơn, ta làm như sau:
– Đầu tiên, ta có bất phương trình ban đầu: x + 3 ≤ 10.
– Bước tiếp theo, ta cần “cô lập” x bằng cách loại bỏ số 3 khỏi vế trái. Ta làm điều này bằng cách trừ 3 từ cả hai vế của bất phương trình: (x + 3) – 3 ≤ 10 – 3.
– Khi thực hiện phép trừ, ta được: x ≤ 7.
– Vậy, tập nghiệm của bất phương trình là tất cả các giá trị của x sao cho x ≤ 7. Điều này có nghĩa là x có thể là bất kỳ số nào không lớn hơn 7.
2. Hệ bất phương trình:
* Ví dụ: Tìm tất cả các số x sao cho -3 < 5 – 2x và 5 – 2x < 9.
Lời giải:
-3 < 5 – 2x
⇒-8 < -2x
⇒ x < 4
Và
5 – 2x < 9
⇒-2x < 4
⇒ x > -2
⇒ x ∈ (-2,4)
Giải thích chi tiết:
Để thỏa mãn cả hai bất phương trình, một số phải có trong cả hai tập nghiệm. Vì vậy, các số thỏa mãn cả hai bất phương trình là các giá trị nằm trong giao của hai tập nghiệm, chính là tập hợp (-2, 4) trong ký hiệu khoảng. Bài toán trên thường được viết dưới dạng bất phương trình kép.
-3 < 5 – 2x < 9 là viết tắt của -3 < 5 – 2x và 5 – 2x < 9.
Lưu ý: Khi ta giải hai bất phương trình riêng biệt thì các bước thực hiện của hai bài toán là như nhau. Vì vậy, ký hiệu bất phương trình kép có thể được sử dụng để giải các hệ phương trình
-3 < 5 – 2x < 9
⇒-8 < -2x < 4
⇒ 4 > x > -2
⇒ x ∈ (-2,4)
Về mặt đồ thị, bài toán này tương ứng với việc tìm các giá trị của x sao cho điểm tương ứng trên đồ thị của y = 5 – 2x nằm giữa hai đồ thị của y = -3 và y = 9.
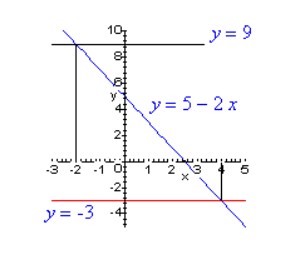
* Bài tập:
Bài 1: Tìm tập nghiệm của bất phương trình 1 < 3 + 5x < 7
Lời giải:
1 < 3 + 5x < 7
⇒ -2 < 5x < 4
⇒ -⅖ < x < ⅘
⇒ x ∈ (-⅖,⅘)
Giải thích chi tiết:
Để giải bất phương trình: 1 < 3 + 5x < 7, ta làm như sau:
– Bước 1: Trừ 3 vào cả ba vế của bất phương trình, ta được:
-2 < 5x < 4
– Bước 2: Chia cả ba vế cho 5, ta được:
-⅖ < x < ⅘
Vậy nghiệm của bất phương trình là x nằm trong khoảng (-⅖,⅘).
Bài 2: Tìm tập nghiệm của hệ bất phương trình 2 – x < 1 hoặc 2 – x > 5
Lời giải:
2 – x < 1
⇒ x > 1
Hoặc
2 – x > 5
⇒ x < -3
⇒ x ∈ (1,+∞) hoặc x ∈ (-∞,-3)
Giải thích chi tiết
Để giải hệ phương trình với các bất phương trình 2 – x < 1 hoặc 2 – x > 5, ta thực hiện các bước sau:
– Bước 1: Giải bất phương trình thứ nhất: 2 – x < 1.
Chuyển vế để tìm x: x > 1.
– Bước 2: Giải bất phương trình thứ hai: 2 – x > 5.
Chuyển vế để tìm x: x < -3.
Vậy, để thỏa mãn hệ phương trình, x cần lớn hơn 1 hoặc nhỏ hơn -3.
3. Bất phương trình chứa giá trị tuyệt đối:
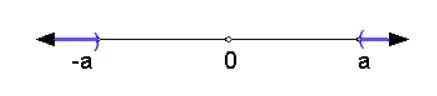
Các bất phương trình chứa giá trị tuyệt đối có thể được viết lại dưới dạng tổ hợp của các bất phương trình. Cho a là một số dương. |x| < a nếu và chỉ nếu -a < x < a. |x| > a nếu và chỉ khi x < -a hoặc x > a. Để hiểu về điều này, hãy nghĩ về một trục số. Giá trị tuyệt đối của một số là khoảng cách từ số đó đến số 0 trên trục số. Vậy bất phương trình |x| < a được thỏa mãn bởi các số có khoảng cách từ 0 nhỏ hơn a. Đây là tập hợp các số giữa -a và a.

Bất đẳng thức |x| > a được thỏa mãn bởi những số có khoảng cách từ 0 lớn hơn a. Điều này có nghĩa là các số lớn hơn a hoặc nhỏ hơn -a.
* Ví dụ: Giải tập nghiệm của bất phương trình | 3 + 2x | ≤ 7
Lời giải:
| 3 + 2x | ≤ 7
⇒-7 ≤ 3 + 2x ≤ 7
⇒-10 ≤ 2x ≤ 4
⇒-5 ≤ x ≤ 2
⇒ x ∈ [-5,2]
Về mặt đồ thị, chúng ta đang tìm các giá trị x sao cho điểm tương ứng trên đồ thị của y = | 3 + 2x | nằm dưới hoặc bằng điểm trên đồ thị y = 7.
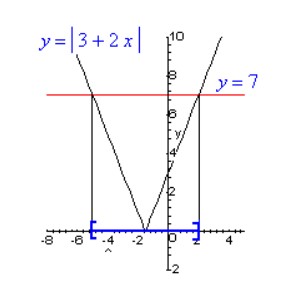
* Bài tập
Bài 1: Tìm tập nghiệm của bất phương trình |3 + x| < 4
Lời giải:
|3 + x| < 4
⇒ -4 < 3 + x < 4
⇒ -7 < x < 1
⇒ x ∈ (-7,1)
Giải thích chi tiết:
Để giải bất phương trình chứa dấu giá trị tuyệt đối |3 + x| < 4, ta sẽ thực hiện theo các bước sau:
– Bước 1: Xác định điều kiện để loại bỏ dấu giá trị tuyệt đối. Ta biết rằng giá trị tuyệt đối của một số là khoảng cách từ số đó đến 0 trên trục số, không phụ thuộc vào dấu của số. Do đó, ta cần xét hai trường hợp: khi 3 + x dương và khi 3 + x âm.
– Bước 2: Giải bất phương trình cho từng trường hợp.
+ Trường hợp 1: Khi 3 + x > 0 (nghĩa là x > -3), ta có |3 + x| = 3 + x. Bất phương trình trở thành 3 + x < 4. Đơn giản hóa, ta được x < 1.
+ Trường hợp 2: Khi 3 + x < 0 (nghĩa là x < -3), ta có |3 + x| = -(3 + x). Bất phương trình trở thành -(3 + x) < 4. Đơn giản hóa, ta được -3 – x < 4, suy ra -x < 7, và cuối cùng là x > -7.
– Bước 3: Kết hợp kết quả từ cả hai trường hợp để tìm tập nghiệm cuối cùng. Tập nghiệm của bất phương trình là giao của hai khoảng (-∞, -3) và (-7, 1), tức là -7 < x < 1.
Vậy, tập nghiệm của bất phương trình |3 + x| < 4 là -7 < x < 1.
Bài 2: Tìm tập nghiệm của bất phương trình |2 – x| > 3
Lời giải:
Để giải bất phương trình chứa dấu giá trị tuyệt đối |2 – x| > 3, ta thực hiện các bước sau:
– Bước 1: Xác định hai trường hợp của giá trị tuyệt đối
+ Trường hợp 1: 2 – x > 0, tức là x < 2
+ Trường hợp 2: 2 – x < 0, tức là x > 2
– Bước 2: Giải bất phương trình cho mỗi trường hợp
Trường hợp 1: |2 – x| = 2 – x
Ta có bất phương trình: 2 – x > 3
Giải ra ta được: x < -1
Trường hợp 2: |2 – x| = -(2 – x)
Ta có bất phương trình: -(2 – x) > 3
Giải ra ta được: x > 5
– Bước 3: Kết hợp nghiệm của cả hai trường hợp
Vậy tập nghiệm của bất phương trình là x < -1 hoặc x > 5.
4. Bất phương trình đa thức:
* Bài tập:
Bài 1: Tìm tập nghiệm của bất phương trình 1.2 x^3 + 3.07 x^2 – x – 3.71 > 0
Lời giải:
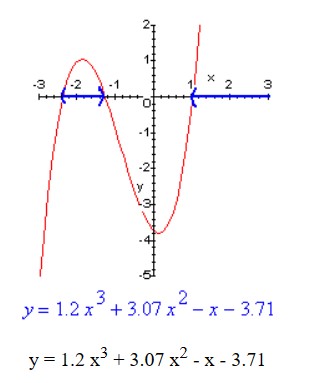
y = 1.2 x^3 + 3.07 x^2 – x – 3.71
Các số tới hạn xấp xỉ -2,35, -1,25 và 1,05. Trong bài toán này, chúng ta tìm kiếm các vùng có đồ thị nằm phía trên trục. Tập nghiệm của bất phương trình là: (-2,35, -1,25) và (1,05, +∞).
Bài 2: Tìm tập nghiệm của bất phương trình x² + 3x – 4 > 0
Lời giải:
Để giải bất phương trình x² + 3x – 4 > 0, ta cần tìm các giá trị của x sao cho biểu thức x² + 3x – 4 có giá trị dương.
Bước đầu tiên là phân tích biểu thức thành nhân tử:
x² + 3x – 4 = (x + 4)(x – 1)
Bây giờ, ta cần xác định các khoảng giá trị của x mà tại đó tích của hai nhân tử này là dương. Điều này xảy ra khi cả hai nhân tử đều dương hoặc cả hai đều âm.
Nhân tử thứ nhất (x + 4) dương khi x > -4 và nhân tử thứ hai (x – 1) dương khi x > 1. Vì vậy, để tích của chúng dương, x phải lớn hơn 1.
Tuy nhiên, nếu cả hai nhân tử đều âm, điều này xảy ra khi x < -4 và x < 1. Nhưng vì không có giá trị nào của x là nhỏ hơn -4 và đồng thời nhỏ hơn 1, nên không có khoảng giá trị nào của x thỏa mãn điều kiện này.
Vậy nên, tập nghiệm của bất phương trình là x > 1.
5. Bất phương trình hữu tỉ:
Bất phương trình hữu tỉ là một dạng đa thức chia cho đa thức. Nói chung, đồ thị của hàm số hữu tỷ có điểm ngắt. Chúng không xác định được khi mẫu số bằng 0. Đây là những chỗ duy nhất có điểm ngắt, vì vậy chúng ta có thể sử dụng kỹ thuật tương tự để giải các bất phương trình hữu tỉ mà chúng ta sử dụng cho các bất phương trình đa thức.
* Bài tập:
Bài 1: Tìm tập nghiệm của bất phương trình x < 1/x
Lời giải:
Để giải bất phương trình x < 1/x, ta cần xét hai trường hợp dựa trên điều kiện của x.
– Trường hợp 1: Nếu x > 0, bất phương trình trở thành x² < 1. Điều này dẫn đến -1 < x < 1.
– Trường hợp 2: Nếu x < 0, bất phương trình trở thành x² > 1. Điều này dẫn đến x < -1.
Kết hợp cả hai trường hợp, ta có tập nghiệm của bất phương trình là x thuộc (-∞, -1) ∪ (-1, 1).
Bài 2: Tìm tập nghiệm của bất phương trình x² – 3x – 11 < x + 10
Lời giải:
Để giải bất phương trình x² – 3x – 11 < x + 10, ta thực hiện các bước sau:
– Chuyển vế các hạng tử để thu được bất phương trình dạng chuẩn: x² – 4x – 21 < 0.
– Phân tích thành nhân tử: (x – 7)(x + 3) < 0.
– Xác định các khoảng nghiệm của bất phương trình từ việc phân tích nhân tử.
– Kết luận nghiệm của bất phương trình là các giá trị x nằm trong khoảng (-3, 7).
Vậy tập nghiệm của bất phương trình là S = {x | -3 < x < 7}.




