Tam giác vuông là gì? Cách chứng minh tam giác vuông?

1. Cách chứng minh Tam giác vuông:

Để chứng minh một tam giác là tam giác vuông có tất cả 5 như sau:

– Chứng minh trong một tam giác có một góc bằng 90 độ

– Chứng minh trong một tam giác có tổng hai góc nhọn bằng 90 độ

– Chứng minh trong một tam giác có bình phương độ dài một cạnh bằng tổng bình phương độ dài hai cạnh kia. Áp dụng định lý Pitago.

– Chứng minh trong một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy.

– Chứng minh trong một tam giác nội tiếp một nửa đường tròn (có 1 cạnh trùng đường kính).

* Cách 1: Để chứng minh một tam giác là tam vuông ta phải chứng minh tam giác đó có tổng 2 góc nhọn bằng 90 độ (2 góc nhọn phụ nhau).

Ví dụ 1: Tam giác ABC có góc C + B = 90°

⇒ Tam giác ABC vuông tại A.

* Cách 2: Để chứng minh một tam giác là tam giác vuông ta chứng minh tam giác đó có bình phương độ dài một cạnh bằng tổng bình phương độ dài hai cạnh còn lại.

Ví dụ 2: Tam giác ABC có AC2 + AB2 = BC2

⇒ Tam giác ABC vuông tại A.

* Cách 3: Để chứng minh một tam giác là tam vuông ta phải chứng minh tam giác đó có đường trung tuyến ứng với bằng nửa cạnh ấy (cạnh huyền).

Ví dụ 3: Tam giác ABC có M là trung điểm BC, biết AM = MB = MC = ½ BC

=> Tam giác ABC vuông tại A.

* Cách 4: Chứng minh trong tam giác có một góc bằng 90 độ (2 góc còn lại tổng bằng 90 độ).

+ Cách chứng minh: Đưa góc cần chứng minh vào góc của một tứ giác rồi chứng minh tứ giác đó là hình chữ nhật, hình vuông, hoặc góc tạo bởi 2 đường chéo của hình thoi, hình vuông.

* Cách 5: Để chứng minh một tam giác là tam vuông ta phải chứng minh tam giác đó nội tiếp đường tròn và có một cạnh là đường kính.

Ví dụ 4: Tam giác MAB nội tiếp đường tròn đường kính AB

=> Tam giác MAB vuông tại M.

2. Định nghĩa về tam giác vuông:

Tam giác vuông là tam giác chỉ có một góc vuông ( tức là 1 góc 90 độ)

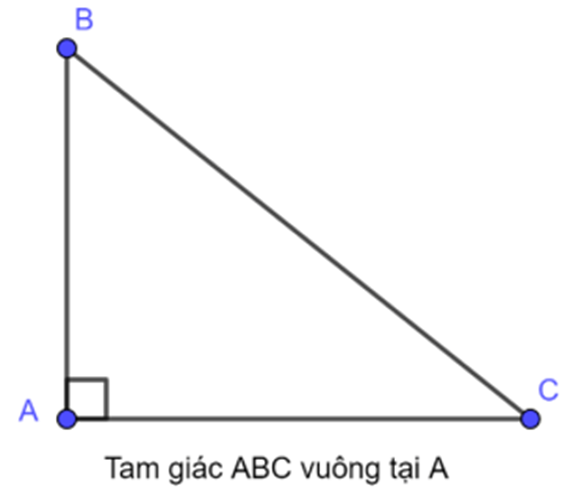
Tam giác ABC vuông tại A:

+ Hai cạnh AB và AC kề với góc vuông gọi là cạnh bên ( hay còn gọi là cạnh góc vuông)

+ Cạnh BC đối diện với góc vuông gọi là cạnh huyền.

3. Định lý Pytago liên quan đến tam giác vuông:

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh còn lại. 

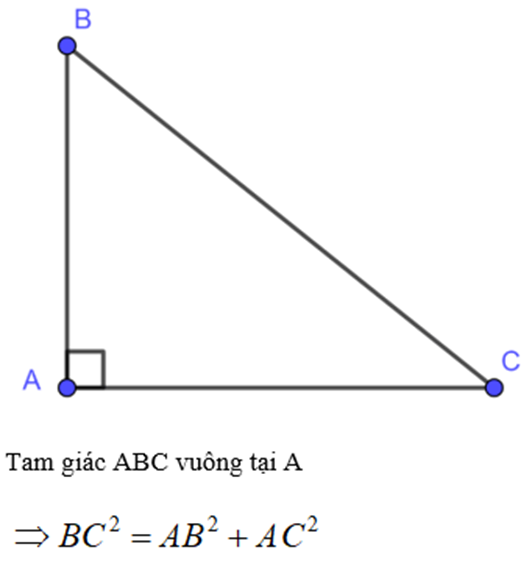
4. Đường trung tuyến trong tam giác vuông:

Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.

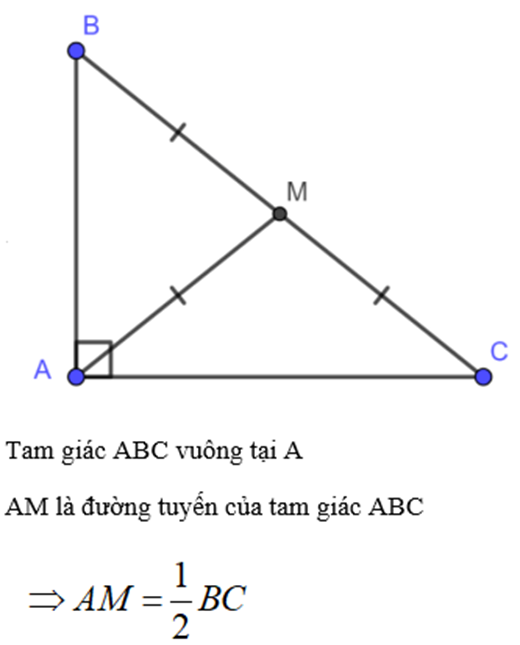
5. Dấu hiệu nhận biết tam giác vuông:

• Tam giác có một góc vuông là tam giác vuông.

• Tam giác có hai góc nhọn phụ nhau là tam giác vuông.

• Tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia là tam giác vuông.

• Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy là tam giác vuông.

• Tam giác nội tiếp đường tròn có một cạnh là đường kính của đường tròn là tam giác vuông.

6. Cách dựng tam giác ABC vuông tại A:

Cho trước cạnh huyền BC = 5 cm và cạnh góc vuông AC = 3 cm.

– Dựng đoạn AC = 3 cm

– Dựng góc CAx bằng 90 độ.

– Dựng cung tròn tâm C bán kinh 5 cm cắt Ax tại B. Nối BC ta có Δ ABC cần dựng.

7. Tính chất của Tam giác vuông:

– Tính chất 1: Trong tam giác vuông, hai góc nhọn phụ nhau (do có 1 góc bằng 90 độ).

Ví dụ: Tam giác DAB vuông tại D

=> Góc A + B = 90°

– Tính chất 2: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh còn lại.

Ví dụ: Tam giác DAB vuông tại D

=> DA2 + DB2 = AB2

– Tính chất 3: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một phần hai cạnh huyền.

Ví dụ: Tam giác DAB vuông tại D có M là trung điểm AB

=> DM = DA = B = ½ AB

8. Bài tập về chứng minh tam giác vuông:

Bài 1: Cho tam giác ABC vuông tại A. Biết AC=57. Đường cao là AH = 15cm. Hãy áp dụng hệ thức lượng trong tam giác vuông, hãy tính HB, HC.

Bài 2: Cho tam giác ABC vuông tại A. Trong đó AB = 12cm, AC = 16cm, phân giác AD, đường cao AM. Tính MD, MB, MC.

Bài 3: Cho ∆ABC vuông tại A. Vẽ đường cao AH, hãy tính chu vi ∆ABC biết AH = 14cm, HB, HC=14.

Bài 4: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 20cm, HC = 9cm. Tính độ dài đường cao AH.

Bài 5: Cho tam giác ABC vuông tại A có BD là đường phân giác góc B. Biết rằng AD = 2cm; BD = 12 cm. Tính độ dài của cạnh BC.

Bài 6: Cho tam giác ABC biết góc B = 60 độ, BC = 8cm; AB + AC = 12cm. Tính độ dài cạnh AB.

Bài 7: Cho hình thang cân ABCD. Trong đó có đáy lớn của hình thang là CD = 10cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên của hình thang. Tính độ dài đường cao của hình thang cân ABCD.

Bài 8: 

a. Cho tam giác ABC biết rằng Góc B = 60 độ, Góc C = 50 độ, AC = 35cm . Hãy tính diện tích tam giác ABC.

b. Cho tứ giác ABCD có góc A = Góc D = 90 độ, Góc C = 40 độ, AB = 4cm, AD=3cm. Hãy tính diện tích tứ giác ABCD.

c. Cho tứ giác ABCD có hai đường chéo cắt nhau tại O. Cho biết AC=4. BD=5, Góc AOB = 50 độ. Tính diện tích tứ giác ABCD bằng công thức lượng giác.

Bài 9: Cho ∆ABC vuông tại A, đường cao là AH, biết rằng chu vi tam giác AHB = 40cm, chu vi tam giác ACH = 5dm. Tính chu vi tam giác ABC và cạnh BH, CH.

Bài 10: Chu vi của một tam giác bằng 120cm. Độ dài các cạnh tỉ lệ lần lượt với 8, 15, 17.

 a) Chứng minh rằng tam giác là một tam giác vuông.

 b) Tính khoảng cách từ giao điểm của ba đường phân giác đến mỗi cạnh của tam giác.

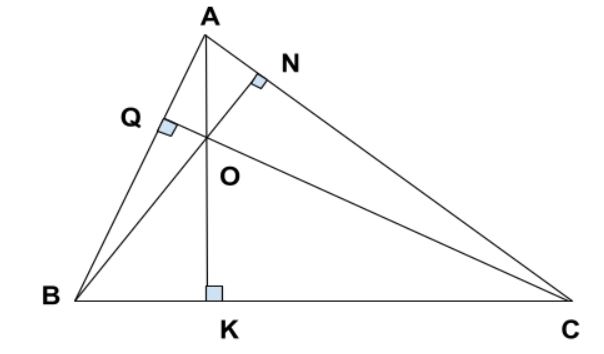
Bài 11: Cho tứ giác lồi ABCD có AB = AC = AD = 10cm, góc B bằng 60 độ và góc A là 90 độ

 a) Tính độ dài đường chéo BD. 

b) Tìm khoảng cách giữa BH và DK từ B và D đến cạnh AC.

c) Tính độ dài HK. 

d) Kẻ BE vuông góc DC kéo dài, tính BE, CE và DC.

Bài 12: Cho tam giác ABC vuông tại A. Trong đó AB = a, AC = 3a. Ở trên cạnh AC lấy các điểm D và E sao cho AD = DE = EC.

 a) Chứng minh DEDB=DBDC.

 b) Chứng minh tam giác BDE đồng dạng với tam giác CDB.

 c) Tính tổng góc AFB + góc BCD

Bài 14: Cho đoạn thẳng AB = 2a. Từ trung điểm M của AB, ta bắt đầu vẽ tia Mx vuông góc với AB. Trên Mx lấy điểm D sao cho OD=a2. Từ B ta tiếp tục vẽ BC vuông góc với đường thẳng AD của tam giác.

 a) Tính độ dài cạnh AD, AC và BC theo a.

 b) Kéo dài DO sao cho ME = a. Chứng minh bốn điểm A, B, C và E cùng nằm trên một đường tròn ( thuộc đường tròn).

Bài 15: Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm.

a. Chứng minh tam giác ABC là tam giác vuông tại A.

b. Kẻ tia phân giác BE của góc B (E thuộc AC), từ E có EP vuông góc với BC (P thuộc BC). Chứng minh EA = EP.

Bài 16: Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính khoảng cách từ trọng tâm G của tam giác ABC đến các đỉnh còn lại của tam giác.

Bài 17: Cho tam giác ABC vuông tại A. Biết AB = 6cm, AC = 8cm. Đường thẳng đi qua trung điểm M của BC và vuông góc với BC cắt AC tại O.

a. Tính độ dài cạnh BC

b. Chứng minh góc CBO bằng góc OCB.

c. Trên tia đối của tia OB lấy điểm F sao cho OF = OC. Chứng minh rằng tam giác BEC vuông.

Bài 18: Cho tam giác ABC vuông tại A, biết AB = 5cm, BC = 13cm

a. Tính độ dài cạnh AC

b. Kẻ AH vuông góc với BC. Tính độ dài 3 cạnh AH, BH, CH.

c. Gọi E là trung điểm BC. Tính độ dài AE

d. Trên tia đối tia EA lấy O sao cho EO = EA. Chứng minh BO = AC và BO // AC

Bài 19: Cho tam giác ABC vuông tại A.

a. Tính độ dài cạnh AC biết AB = 5cm và BC = 13cm

b. Trên cạnh BC lấy điểm E sao cho BE = BA. Đường thẳng đi qua E cắt AC tại I sao cho IE vuông góc với BC tại E. So sánh 2 góc ABI và góc CBI

c. Nếu tam giác ABC có góc A = 30O và EC = 6cm. Hãy tính chu vi của tam giác ABC

Bài 20:

Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.

a) Chứng minh rằng tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.

b) Hỏi rằng điểm M nằm ở đâu thì diện tích tam giác MBC bằng diện tích tam giác ABC?