Hình elip là quỹ tích của tất cả các điểm trong mặt phẳng sao cho tổng khoảng cách của chúng đến hai điểm cố định trong mặt phẳng là không đổi. Phương trình chính tắc là một dạng phương trình để biểu diễn đường thẳng trong mặt phẳng tọa độ Oxy. Dưới đây là hướng dẫn cách viết phương trình chính tắc của Elip.
Mục lục bài viết
1. Hướng dẫn cách viết phương trình chính tắc của Elip:
Phương trình chính tắc là một dạng phương trình để biểu diễn đường thẳng trong mặt phẳng tọa độ Oxy. Phương trình chính tắc của đường thẳng có dạng:
Trong đó, (x0, y0) là tọa độ của một điểm nằm trên đường thẳng, t là tham số và (x, y) là tọa độ của các điểm khác trên đường thẳng. Phương trình chính tắc còn được gọi là phương trình tham số vì nó biểu diễn các tọa độ x, y qua một tham số t. Phương trình chính tắc có ưu điểm là dễ dàng xác định được vector chỉ phương của đường thẳng và không bị giới hạn bởi các trường hợp đặc biệt như đường thẳng song song với trục tung hay trục hoành.
Phương trình này được sử dụng nhiều trong giải tích hình học để giải quyết các bài toán liên quan đến giao điểm, khoảng cách, góc giữa các đường thẳng hay các hình học khác như tam giác, tứ giác, đường tròn, elip, parabol, hyperbol…
Khi tâm của hình elip nằm ở gốc tọa độ (0,0) và các tiêu điểm nằm trên trục x và trục y, thì chúng ta có thể dễ dàng rút ra phương trình elip.
Phương trình của hình elip được cho bởi;
x2/a2 + y2/b2 = 1
1.1. Đạo hàm của phương trình Elip:
ãy xem nó có nguồn gốc như thế nào.
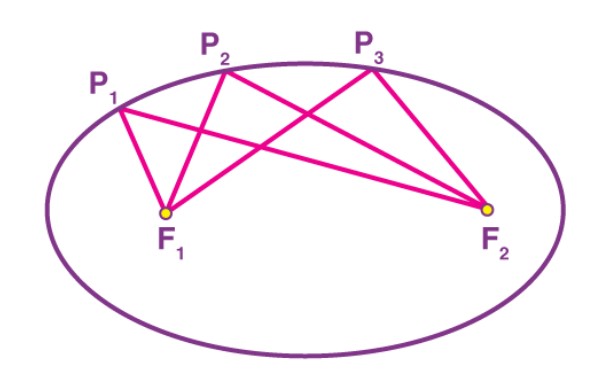
Hình trên biểu thị một hình elip sao cho P1F1 + P1F2 = P2F1 + P2F2 = P3F1 + P3F2 là một hằng số. Hằng số này luôn lớn hơn khoảng cách giữa hai tiêu điểm. Khi cả hai tiêu điểm được nối với sự trợ giúp của một đoạn đường thì điểm giữa của đoạn đường này nối các tiêu điểm được gọi là tâm, O đại diện cho tâm của hình elip trong hình dưới đây:
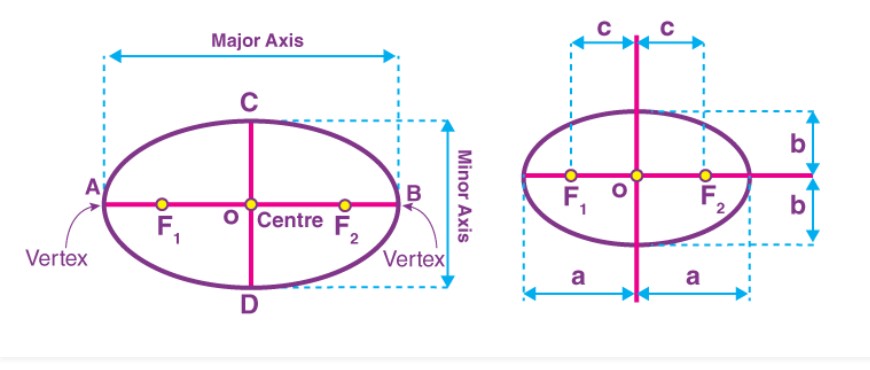
Đoạn thẳng đi qua tiêu điểm của elip là trục chính, đoạn thẳng vuông góc với trục chính và đi qua tâm elip là trục nhỏ. Các điểm cuối A và B như được hiển thị được gọi là các đỉnh biểu thị giao điểm của các trục chính với hình elip. ‘2a’ biểu thị độ dài của trục chính và ‘a’ là độ dài của bán trục lớn. ‘2b’ là độ dài của trục nhỏ và ‘b’ là độ dài của bán trục nhỏ. ‘2c’ biểu thị khoảng cách giữa hai tiêu điểm.
1.2. Chứng minh:
Chúng ta hãy xét các điểm cuối A và B trên trục chính và các điểm C và D ở cuối trục nhỏ.
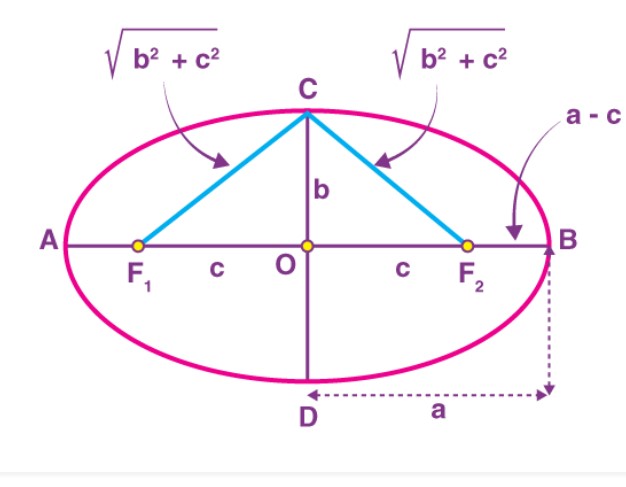
Tổng khoảng cách của B đến F1 là F1B + F2B = F1O + OB + F2B
⇒ c + a + a – c = 2a
Tổng khoảng cách từ điểm C đến F1 là F1C + F2C
⇒ F1C + F2C = √(b2 + c2) + √(b2 + c2) = 2√(b2 + c2)
Theo định nghĩa của hình elip;
2√(b2 + c2) = 2a
⇒a = √(b2 + c2)
⇒ a2 = b2 + c2
⇒c2 = a2 – b2
Các trường hợp đặc biệt:
– Nếu c = 0 thì F1 và F2, tức là cả hai tiêu điểm đều hợp nhất với tâm của hình elip. Ngoài ra a2 sẽ bằng b2, tức là a = b nên bây giờ chúng ta có một đường tròn trong trường hợp này.
Nếu c = a thì b trở thành 0 và ta được đoạn thẳng F1F2.
2. Phương trình chuẩn của Elip:
Phương pháp đơn giản nhất để xác định phương trình của một hình elip là giả sử rằng tâm của hình elip nằm ở gốc tọa độ (0, 0) và các tiêu điểm nằm trên trục x hoặc trục y của mặt phẳng Cartesian.
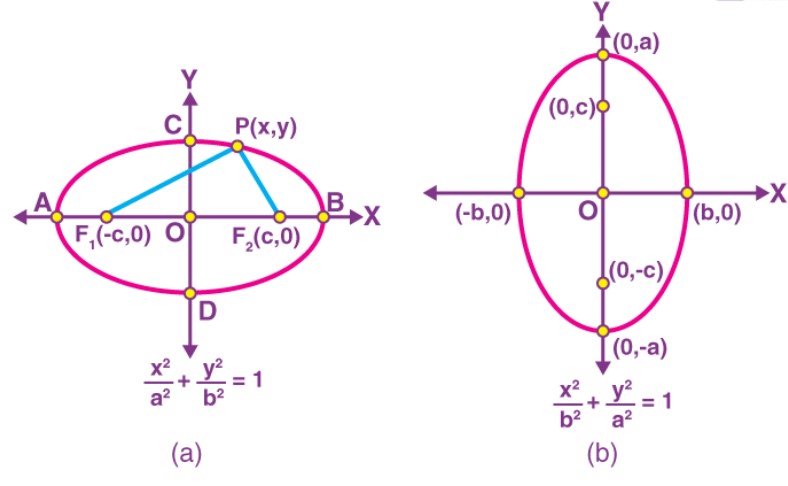
Cả hai tiêu điểm đều nằm trên trục x và tâm O nằm ở gốc tọa độ.
Chúng ta hãy xét hình (a) để suy ra phương trình của một hình elip. Đặt tọa độ của F1 và F2 lần lượt là (-c, 0) và (c, 0) như hình vẽ. Chúng ta hãy xét một điểm P(x, y) nằm trên hình elip sao cho P thỏa mãn định nghĩa, tức là tổng khoảng cách của P đến F1 và F2 trong mặt phẳng là hằng số 2a.
⇒ PF1 + PF2 = 2a – – – (1)
Sử dụng công thức khoảng cách, khoảng cách có thể được viết là:
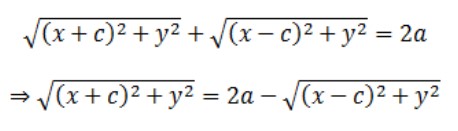
Bình phương và rút gọn cả hai vế ta được;
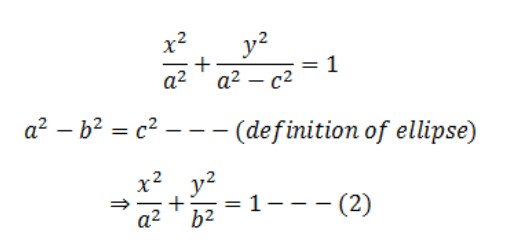
Bây giờ vì P nằm trên hình elip nên nó phải thỏa mãn phương trình 2 sao cho 0 < c < a.
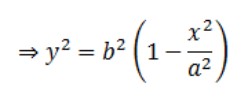
Vì vậy,
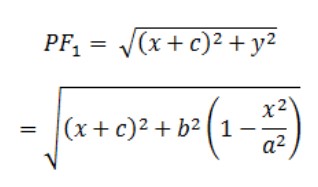
Về việc đơn giản hóa,
PF1 = a + (c/a)x
Tương tự,
PF2 = a – (c/a)x
Vì thế,
PF1 + PF2 = 2a
Do đó phương trình của hình elip có tâm tại gốc và trục chính dọc theo trục x là:
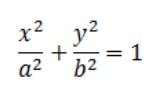
trong đó –a ≤ x ≤ a.
Tương tự, phương trình của hình elip có tâm tại gốc và trục chính dọc theo trục y là:
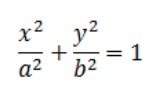
nơi có –b ≤ y ≤ b.
3. Hình Elip:
Hình elip là một đường cong phẳng xung quanh hai tiêu điểm, sao cho với mọi điểm trên đường cong, tổng khoảng cách đến hai tiêu điểm là hằng số. Hình tròn là trường hợp đặc biệt của đường elip khi hai tiêu điểm trùng nhau. Độ dẹt của hình elip được biểu diễn bằng tâm sai e của nó, chạy từ e = 0 (trường hợp của đường tròn) đến e = 1 (độ dẹt vô hạn, không còn là elip mà là một parabol ).
* Hình elip được xác định bởi hai trục của nó dọc theo trục x và y:
– Trục chính là đường kính dài nhất của hình elip (thường được ký hiệu là ‘a’), đi qua tâm từ đầu này đến đầu kia, ở phần rộng của hình elip. Trong khi đó trục nhỏ là đường kính ngắn nhất của hình elip (ký hiệu là ‘b’), đi qua tâm ở phần hẹp nhất.
– Một nửa trục lớn gọi là bán trục lớn và một nửa trục nhỏ gọi là bán trục nhỏ.
* Hình elip có nhiều tính chất quan trọng, ví dụ như:
– Hai trục lớn và nhỏ của hình elip cắt nhau ở tâm và đều bằng nhau về độ dài.
– Khoảng cách từ tâm đến các điểm trên đường elip là như nhau và bằng độ dài trục lớn.
– Diện tích hình elip được tính bằng công thức S = π*a*b, trong đó a và b lần lượt là độ dài nửa trục lớn và nửa trục nhỏ của elip.
– Hình elip có thể được tạo thành bằng cách xoay một hình cầu quanh trục không trùng với đường kính của nó.
– Hình elip có thể được xác định bằng một tiêu điểm và một đường thẳng nằm ngoài elíp gọi là đường chuẩn: elíp là quỹ tích các điểm có tỉ số khoảng cách tới tiêu điểm và đường chuẩn là hằng số.
– Hình elip rất thông dụng trong vật lý, thiên văn và kỹ thuật. Ví dụ, quỹ đạo của mỗi hành tinh trong hệ Mặt Trời gần giống một hình elíp với Mặt Trời là một tiêu điểm.
.* Độ lệch tâm của hình elip
Tỷ lệ khoảng cách từ tâm của hình elip từ tiêu điểm đến bán trục lớn của hình elip được xác định là độ lệch tâm của hình elip.
Độ lệch tâm của hình elip, e = c/a
Trong đó c là tiêu cự và a là chiều dài bán trục lớn.
Vì c ≤ a nên độ lệch tâm luôn nhỏ hơn 1 trong trường hợp hình elip.
Mà, c2 = a2 – b2
Do đó, độ lệch tâm trở thành:
e = √(a2 – b2)/a
e = √[(a2 – b2)/a2] e = √[1-(b2/a2)]
* Làm thế nào để vẽ một hình elip?
Để vẽ một hình elip trong toán học, cần phải tuân theo một số bước nhất định. Phương pháp từng bước để vẽ một hình elip có kích thước cho trước được đưa ra dưới đây.
– Quyết định chiều dài của trục chính sẽ là bao nhiêu, vì trục chính là đường kính dài nhất của hình elip.
– Vẽ một đường ngang theo chiều dài của trục chính.
– Đánh dấu điểm giữa bằng thước kẻ. Điều này có thể được thực hiện bằng cách lấy chiều dài của trục chính và chia nó cho hai.
– Xây dựng một vòng tròn có đường kính này bằng một la bàn.
– Quyết định độ dài của trục nhỏ sẽ là bao nhiêu, vì trục nhỏ là đường kính ngắn nhất của hình elip.
– Bây giờ, tại điểm giữa của trục chính, bạn lấy thước đo góc và đặt gốc tọa độ của nó. Ở 90 độ, đánh dấu điểm. Sau đó xoay 180 độ bằng thước đo góc và đánh dấu vị trí. Bây giờ bạn có thể vẽ trục nhỏ giữa hoặc trong hai điểm tại điểm giữa của nó.
– Vẽ một vòng tròn có đường kính này bằng compa như chúng ta đã làm với trục chính.
– Dùng compa để chia toàn bộ hình tròn thành 12 phần 30 độ. Đặt thước đo góc của bạn trên trục chính ở điểm gốc và dán nhãn các khoảng 30 độ bằng các dấu chấm sẽ thực hiện được điều này.
– Sau đó, bằng các đường kẻ, bạn có thể liên kết các dấu chấm ở giữa.
– Vẽ các đường ngang (trừ trục chính và trục phụ) từ vòng tròn bên trong.
– Chúng song song với trục chính và từ tất cả các điểm nơi đường tròn bên trong và đường 30 độ hội tụ, chúng đi ra ngoài.
– Hãy thử vẽ các đường ngắn hơn một chút ở gần trục phụ nhưng hãy vẽ chúng dài hơn một chút khi bạn di chuyển về phía trục chính.
– Vẽ các đường thẳng đứng (trừ trục chính và trục phụ) từ vòng tròn bên ngoài.
– Chúng song song với trục nhỏ và từ tất cả các điểm nơi đường tròn bên ngoài và đường 30 độ hội tụ, chúng đi vào trong.
– Cố gắng vẽ các đường dài hơn một chút ở gần trục phụ, nhưng khi bạn bước về phía trục chính, hãy vẽ chúng ngắn hơn một chút.
– Bạn có thể lấy thước kẻ và kéo giãn ra một chút trước khi vẽ đường thẳng đứng nếu phát hiện đường ngang quá xa.
– Hãy cố gắng hết sức bằng cách vẽ tự do để vẽ các đường cong giữa các điểm bằng tay.




