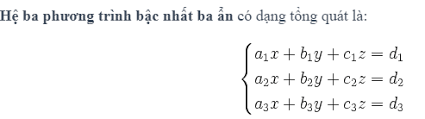Công thức và cách tính góc giữa hai vecto kèm bài tập

11/09/202411/09/2024

11/09/2024

Góc giữa 2 vecto: là góc ngắn nhất mà tại đó quay bất kỳ của hai vecto nào về vecto kia với điều kiện cả hai vecto có cùng phương. Để nắm chắc kiến thức cũng như ôn tập tốt về góc giữa hai vecto, mời các bạn tham khảo bài viết Công thức và cách tính góc giữa hai vecto kèm bài tập dưới đây.

Mục lục bài viết

1 1. Công thức và cách tính góc giữa hai vecto:
2 2. Phương pháp nào được áp dụng trong hệ tọa độ để tính cosin (cos) góc giữa hai vectơ?
3 3. Bài tập vận dụng có đáp án:

1. Công thức và cách tính góc giữa hai vecto:

Công thức tính góc giữa 2 vecto là công thức cosin (cos) của góc giữa hai vecto trong mặt phẳng. Để tính góc giữa 2 vecto, ta cần tính tích vô hướng của chúng và độ dài của từng vecto.

Bước 1: Tính tích vô hướng của hai vecto a và b bằng công thức: a·b = |a| |b| cos(θ)

Trong đó, |a| và |b| là độ dài của từng vecto, cos(θ) là góc giữa hai vecto a và b.

Bước 2: Tính độ dài của từng vecto a và b. Đối với vecto a, tính độ dài bằng cách tính căn bậc hai của tổng các thành phần của vecto a bình phương: |a| = √(a₁² + a₂² + a₃²)

Tương tự, tính độ dài của vecto b.

Bước 3: Áp dụng công thức cosin (cos) để tính góc giữa hai vecto: cos(θ) = (a·b) / (|a| |b|)

Trong đó, (a·b) là tích vô hướng của hai vecto a và b được tính ở bước 1, |a| và |b| là độ dài của từng vecto được tính ở bước 2.

Bước 4: Sử dụng công thức cơ bản của cosin (cos) để tính góc: θ = arccos(cos(θ))

Ở đây, arccos là hàm nghịch đảo của cosin (cos) và được tính bằng sử dụng hàm nghịch đảo trên máy tính hoặc bằng sử dụng bảng giá trị của cosin (cos).

Ví dụ: Giả sử chúng ta có hai vecto a = (2, 3, 4) và b = (1, 5, -2). Để tính góc giữa hai vecto này, ta thực hiện các bước như sau:

1. Tính tích vô hướng của hai vecto a và b: a·b = (2*1) + (3*5) + (4*(-2)) = 2 + 15 – 8 = 9

2. Tính độ dài của vecto a và b:

|a| = √(2² + 3² + 4²) = √(4 + 9 + 16) = √29

|b| = √(1² + 5² + (-2)²) = √(1 + 25 + 4) = √30

3. Áp dụng công thức cosin (cos): cos(θ) = (a·b) / (|a| |b|) = 9 / (√29 * √30)

4. Tính góc giữa hai vecto: θ = arccos(cos(θ))

2. Phương pháp nào được áp dụng trong hệ tọa độ để tính cosin (cos) góc giữa hai vectơ?

Phương pháp được áp dụng trong hệ tọa độ để tính cosin (cos) góc giữa hai vectơ là sử dụng công thức tính cos (cosin) của góc giữa hai vectơ trong mặt phẳng với hệ trục tọa độ vuông góc Oxy và trong không gian với hệ trục Oxyz.

Công thức được sử dụng để tính cos (cosin) góc giữa hai vectơ A và B là: cos(θ) = (A·B) / (||A||·||B||)

Trong đó, A·B là tích vô hướng của hai vectơ A và B, ||A|| là độ dài của vectơ A và ||B|| là độ dài của vectơ B.

Đầu tiên, tính tích vô hướng của hai vectơ A và B bằng cách nhân các thành phần tương ứng của hai vectơ lại với nhau và cộng kết quả lại: A·B = A1*B1 + A2*B2 + A3*B3

Tiếp theo, tính độ dài của vectơ A bằng cách tính căn bậc hai của tổng bình phương các thành phần của vectơ A:

||A|| = √(A1^2 + A2^2 + A3^2)

Tương tự, tính độ dài của vectơ B:

||B|| = √(B1^2 + B2^2 + B3^2)

Sau đó, thay các giá trị đã tính vào công thức cos(θ) = (A·B) / (||A||·||B||) để tính cosin (cos) của góc giữa hai vectơ A và B.

Với phương pháp này, ta có thể tính được góc giữa hai vectơ trong hệ tọa độ.

3. Bài tập vận dụng có đáp án:

Bài 1: Cho hai vecto khác vecto . Khẳng định nào sau đây đúng?

A. Hai vecto cúng phương khi và chỉ khi giá chủa chúng song song với nhau

B. Hai vecto cùng phương khi và chỉ khi giá của chúng trùng nhau

C. Nếu hai vecto cùng phương thì chúng cùng hướng

D. Hai vecto cùng phương khi và chỉ khi giá của chúng song song hoặc trùng nhau.

Đáp án: D. Hai vecto cùng phương khi và chỉ khi giá của chúng song song và bằng nhau.

Bài 2: Nếu hai vecto cùng ngược hướng với một vecto thứ ba (và cả 3 vecto đều khác vecto không) thì ba vecto đó:

A. Cùng hướng

B. Cùng độ dài

C. Bằng nhau

D. Ngược hướng

Đáp án: chọn A. Nếu hai vecto cùng ngược hướng với một vecto thứ ba và cả ba vecto đề khác vecto không thì ba vecto đó bằng nhau.

Bài 3: Gọi G là trọng tâm tam giác vuông ABC với cạnh hyền BC = 12. Vecto có độ dài bằng bao nhiêu?

A. Độ dài bằng 2

B. Độ dài bằng 4.

C. Độ dài bằng 8

D. Độ dài bằng 5

Đáp án: Chọn A. Vecto có độ dài bằng 2

Bài 4: Chọn khẳng định đúng:

A. Hai vecto có giá vuông góc thì cùng phương

B. Hai vecto cùng phương thì chúng ngược hướng

C. Hai vecto cùng phương thì giá của chúng song song hoặc trùng nhau

D. Hai vecto cùng ngược hướng với 1 vecto thứ ba thì cùng hướng

Bài 5: Cho hai vecto có độ dài bằng 1 và thoả mãn điều kiện, Tính góc giữa 2 vecto

a. 30 độ

B. 60 độ

C. 90 độ

D. 120 độ

Đáp án bài 6: Chọn D, ta có cosa = -1/2 => góc giữa 2 vecto bằng 120 độ (áp dụng lý thuyết bình phương cô hướng bằng bình phương độ dài).

Đáp án bài 5: Chọn C. Hai vecto cùng phương thì giá của chúng song song hoặc trùng nhau là khẳng định đúng.

Bài 6: Giả sử và lần lượt là vecto chỉ chỉ phương của 2 đường thẳng a và b. Giả sử . Tính góc giữa a và b

A. -30 độ

B. 30 độ

C. 150 độ

D. 170 độ

Đáp án: D. Góc giữa a và b là 170 độ

Bài 7: Tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và đều có độ dài là I. Gọi M là trung điểm của canh AB, Góc giữa hai vecto bằng:

A. 0 độ

B. 45 độ

C. 60 độ

D. 120 độ

Đáp án: Chọn D. 120 độ

Bài 8: Cho hình chóp S.ABCD có đấy là hình vuộng cạnh a√2, SA vuông góc với mặt phẳng đáy tại A, SA = a√2 . Góc giữa đường thẳng SC và mặt phẳng ABCD

A. 20 độ

B. 30 độ

C. 45 độ

D. 60 độ

Đáp án, Chọn B. Góc giữ đường thẳng SC và mặc phảng ABCD là 30 độ.

Lời giải chi tiết:

Ta có SA vuông góc với mặt phẳng ABCD nên AC là hình chiếu của SC trên mặt phẳng ABC. Do đó góc giữa SC và mặt phẳng ABCD bằng góc của SC và AC bằng góc SCA.

Xet hình vuôn ABCD, ta có AC = a√6

Xét tam giác SAC vuông tại A, ta có => = 30 độ

Bài 9: Cho hình chíp S.ABCD có đấy ABCD là hình bình hành với BC = 2a, SA vuông góc với mặt phẳng đáy, Góc giữa hai đườn thẳng SD và BC nằm trong khoảng nào

A. (20^o; 30^o)

B. (40^o; 50^o)

C. (30^o; 40^o)

D. (50^o; 60^o)

Lời giải chi tiết: Đáp án D. (50; 60)

Ta có BC // AD <=> góc (SD, BC) = góc SDA ( Do tam giác SAD vuông tạ A nên góc SDA < 90 độ)

Xét tam giác SAD vuông tại A, ta có tan = SA/AD = 3a/2a =3/2 => góc SDA xấp xỉ 56 độ và nằm trong khoảng (50^o; 60^o)

Bài 10: Cho tứ diện ABCD có AC = BD = 2a. Gọi M, N lần lượt là trung điểm BC, AD. Biết tằng MN = a√6. Tính góc giữa AC và BD.

A . 30 độ

B. 45 độ

C. 60 độ

D. 90 độ

Lời giải chi tiết: Chọn đáp án C. 60 độ

Gọi I là trung điểm của AB, ta có IM = IN = a

Áp dụng định lý của cossin cho tam giác IMN ta có: góc MIN bằng 120 độ => góc giữa AC và BD bằng 60 độ.

Bài 11: Cho hình chóp đều S.ABCD có cạnh đáy a√2, canh bên 2a. Góc giữa cạnh bên và mặt đáy bằng

A. 30 độ

B. 45 độ

C. 60 độ

D. 90 độ

Lời giải chi tiết: Chọn đáp án C. 60 độ

Ta có góc giữa cạnh bên và mặt đáy alf góc giữa SD và (ABCD). Gọi O là giao điểm của AC và BD. Vì A.ABCD là hình chóp đều nên SO vuông góc với mặt phẳng ABCD.

=> OD là hình chiếu cua SD trên mặt phảng ABCD

Do đó góc giữa SD và mặt phảng ABCD là góc SDO

Xát hình vuông ABCD có OD = BD/2 = a

Xét tam giác SOD vuông tại O => góc SDO bằng 60 độ

Trên đây là bài viết của Luật Dương Gia về Công thức và cách tính góc giữa hai vecto kèm bài tập thuộc chủ đề Toán lớp 10, thư mục Toán học. Mọi thắc mắc pháp lý, vui lòng liên hệ Tổng đài Luật sư 1900.6568 hoặc Hotline dịch vụ 037.6999996 để được tư vấn và hỗ trợ.