Tài liệu bao gồm các dạng Toán về trung điểm của đoạn thẳng và cách giải chi tiết cho từng bài tập cho các em học sinh tham khảo, ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán lớp 6 phần Hình học Chương 1. Mời các bạn cùng tham khảo và tải tài liệu tại đây.
Mục lục bài viết
1. Kiến thức cần nhớ:
– Trung điểm M của đoạn thẳng AB là điểm nằm giữa A, B và cách đều hai điểm này (MA = MB)
Cho một đoạn thẳng, yêu cầu tìm trung điểm của đoạn thẳng đó (có thể cho biết số đo hoặc không biết số đo của đoạn thẳng đó).
– Cách xác định trung điểm của đoạn thẳng: Để xác định trung điểm M của AB thì ta dùng thước đo độ dài đoạn AB rồi xác định vị trí điểm M nằm giữa A , B và chia đoạn AB thành hai đoạn bằng nhau.
2. Các dạng Toán về trung điểm của đoạn thẳng lớp 6:
Dạng 1. Nhận biết một điểm là trung điểm của đoạn thẳng
Phương pháp giải
Vận dụng định nghĩa trung điểm của đoạn thẳng. Để chứng tỏ M là trung điểm của AB, phải có đủ để
hai điều kiện :
– M nằm giữa A và B (hoặc AM + MB = AB)
– MA = MB.
Ví dụ 1. (Bài 60 trang 125 SGK)
Trên tia Ox, vẽ hai điểm A, B sao cho OA = 2cm ; OB = 4cm.
a) Điểm A có nằm giữa hai điểm o và B không ?
b) So sánh OA và AB.
c) Điểm A có là trung điểm của đoạn thẳng OB không ? Vì sao ?
Giải
a) Điểm A nằm giữa O và B vì A và B đều nằm trên tia Ox và OA < OB.
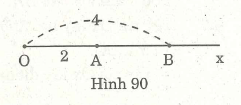
b) Điểm A nằm giữa O và B nên :
OA + AB = OB;
AB = OB – OA = 4 – 2 = 2 (cm)
Vậy : OA = AB.
c) Điểm A là trung điểm của OB vì A nằm giữa O và B và OA = AB.
Ví dụ 2. (Bài 61 trang 126 SGK)
Cho hai tia đối nhau Ox, Ox’. Trên tia Ox vẽ điểm A sao cho OA = 2cm. Trên tia Ox’ vẽ điểm B sao cho
OB = 2cm. Hỏi O có là trung điểm của đoạn thẳng AB không ? Vì sao ?
Giải
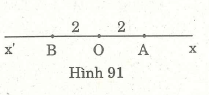
Hai tia OA, OB đối nhau nên O nằm giữa A và B. Lại có OA = OB = 2cm nên O là trung
điểm của AB.
Ví dụ 3. (Bài 62 trang 126 SGK)
Gọi O là giao điểm của hai đường thẳng xx’, yy’. Trên xx’ vẽ đoạn thẳng CD dài 3cm, trên yy‘ vẽ đoạn
thẳng EF dài 5cm sao cho o là trung điểm chung của cả hai đoạn thẳng ấy.
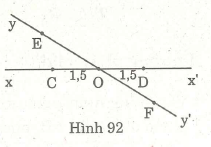
Hướng dẫn
Trên tia Ox vẽ điểm C sao cho : OC = 3:2 = 1,5 (cm).
Bạn đọc tự vẽ các điểm D, E , F.
Ví dụ 4. (Bài 64 trang 126 SGK)
Cho đoạn thẳng AB dài 6cm. Gọi c là trung điểm của AB. Lấy D và E là hai điểm thuộc đoạn thẳng AB
sao cho AD = BE = 2cm . Vì sao C là trung điểm của DE ?
Giải
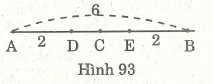
Vì C là trung điểm của AB nên C nằm giữa A, B (1) và CA = CB = 6:2 = 3(cm).
Trên tia AB có : AD < AC (2 < 3) nên điểm D nằm giữa A và c (2) do đó :
CD = AC – AD = 3 – 2 = 1(cm).
Lập luận tương tự ta được điểm E nằm giữa B và c (3) và CE = 1 cm .
Từ (1), (2), (3) suy ra điểm C nằm giữa D và E . Mặt khác có:
CD = CE (= 1 cm) nên c là trung điểm của DE.
Ví dụ 5 . Cho điểm o nằm giữa hai điểm A và B sao cho AO = 1/2 AB .
Chứng tỏ rằng O là trung điểm của AB.
Giải
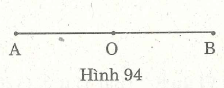
Điểm O nằm giữa A và B (1) nên :
AO + OB = AB ; OB = AB – OA ;
OB = AB – 1/2AB = 1/2 AB.
Do đó OA = OB (2).
Từ (1) và (2) suy ra o là trung điểm của AB.
Ví dụ 6 . Vẽ đoạn thẳng AB = 6cm. Điểm c nằm giữa A và B sao cho
AC = 1/3 AB. Điểm o nằm trên tia CB sao cho CO = 1/2 AC.
Chứng tỏ rằng O là trung điểm của AB.
Giải
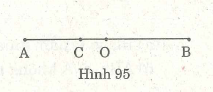
AC = 1/3 .6 = 2(cm); CO = 1.2 .2 = 1 (cm)
Hai tia CA , CO đối nhau nên C nằm giữa A và O do đó :
AO = AC + CO = 2 + 1 = 3(cm).
Trên tia AB có AO < AB (3 < 6) nên O nằm giữa A và B, mặt khác
AO = 1/2 AB nên o là trung điểm của AB . *
Dạng 2. Chọn câu trả lời đúng, điều vào chỗ trống
Phương pháp giải
Chọn câu bao gồm đủ hai điều kiện của định nghĩa trung điểm của đoạn thẳng.
Ví dụ 7. (Bài 63 trang 126 SGK)
Khi nào ta kết luận được điểm I là trung điểm của đoạn thẳng AB ? Em hãy chọn những câu trả lời
đúng trong các câu trả lời sau :
a) Cho biết IA = IB ;
b) Cho biết AI + IB = AB ;
c) Cho biết AI + IB = AB và IA = IB ;
d) Cho biết IA = IB = AB/2 .
Hướng dẫn
Câu c), câu d) đúng.
Ví dụ 8. (Bài 65 trang 126 SGK)
Xem hình 96. Đo các đoạn thẳng AB, BC, CD, CA rồi điền vào chỗ trống trong các phát biểu sau :
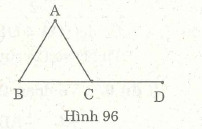
a) Điểm C là trung điểm của … vì…
b) Điểm C không là trung điểm của … vì C không thuộc đoạn thẳng AB.
c) Điểm A không là trung điểm của BC vì…
Hướng dẫn
a) BD vì C nằm giữa B, D và CB = CD (= 2,5 cm);
b) AB ;
c) A không nằm giữa B và C .
Dạng 3. Tính độ dài đoạn thẳng
Phương pháp giải
Dựa vào nhận xét : khoảng cách từ trung điểm của đoạn thẳng đến mỗi đầu đoạn thẳng bằng nửa độ
dài của đoạn thẳng ấy.
Ví dụ 9. Cho đoạn thẳng AB. Gọi M và N lần lượt là trung điểm của AB và AM. Giả sử AN = l,5cm.
Tính AB.
Hướng dẫn
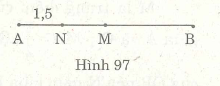
Trước hết tính AM được AM = 3cm, sau đó tính AB được AB = 6cm.
Ví dụ 10. Cho đoạn thẳng AB và trung điểm M của nó. Lấy điểm o nằm giữa A và M.
Hãy chứng tỏ rằng OM = (OB – OA)/2.
Giải
Điểm o nằm giữa A và M nên AO < AM;
M là trung điểm của AB nên AM = MB < AB.
Suy ra AO < AM < AB,
Do đó M nằm giữa o và B, ta có OM = OB – MB (1)
Mặt khác OM = MA – OA (2)
Từ (1) và (2) suy ra OM + OM = OB – MB + MA – OA hay
2OM = OB – OA, do đó OM= (OB – OA)/2.
Dạng 4. Tìm trung điểm của đoạn thẳng
Phương pháp giải
Xét từng điểm, chọn điểm nào thỏa mãn định nghĩa trung điểm của đoạn thẳng.
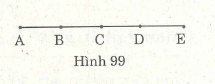
Ví dụ 11. Tìm trên hình 99, những điểm là trung điểm của đoạn thẳng,
biết rằng AB = BC = CD = DE.
Hướng dẫn
B là trung điểm của đoạn thẳng AC;
C là trung điểm của đoạn thẳng BD; AE;
D là trung điểm của đoạn thẳng CE.
Ví dụ 12. Cho điểm O nằm giữa A và B. Gọi M và N thứ tự là trung điểm của OA và OB.
Biết AB = a, tính MN.
Giải

M là trung điểm của OA nên M nằm
giữa A và O ; MO = 1/2 AO . N là trung điểm của OB nên N nằm giữa B và O ; ON = 1/2 OB.
Ta lại có O nằm giữa A và B (đề bài) nên O nằm giữa M và N. Suy ra :
MN = MO + ON = (AO+OB)/2 = AB/2 = a/2.
3. Bài tập vận dụng:
Bài 1: Gọi M là trung điểm của đoạn thẳng AB. Tính độ dài hai đoạn thảng AM và MB, biết AB = 4cm.
Bài 2: Gọi C là trung điểm của đoạn thẳng AB. Tính độ dài hai đoạn thảng AC và BC, biết AB= 6cm.
Bài 3: Cho điểm O thuộc đường thẳng xy. Trên tia Ox lấy điểm M sao cho OM = 4cm. Trên tia Oy lấy điểm N sao cho ON=2cm. Gọi A, B lần lượt là trung điểm của OM và ON.
a) Chứng tỏ O nằm giữa A và B.
b) Tính độ dài đoạn thẳng AB.
Bài 4: Cho Ox và Oy là hai tia đối nhau. Trên tia Ox lấy điểm A sao cho OA = 6cm. Trên tia Oy lấy điểm B sao cho OB=3cm. Gọi M vàN lần lượt là trung điểm của OA và OB.
a) Tong ba điểm M,O,N điểm nào nằm giữa hai điểm còn lại? Vì sao?
b) Tính độ dài các đoạn thẳng OM, ON và MN.
Bài 5: Trên Ox lấy hai điểm A,B sao cho OA=2cm, OB =6cm. Gọi M là trung điểm của đoạn thẳn OB.
a) Tính độ dài đoạn thẳng AB.
b) Chứng tỏ A nằm giữa O và M.
c) Tính đọ dài AM.
Bài 6: Trên tia Ox, lấy hai điểm A và B sao cho OA= 4cm, OB = 6cm. Gọi M là trung điểm của đoạn thẳng OB.
a) Tinh độ dài AB.
b) Chứng tỏ M nằm giữa hai điểm O và A.
Bài 7: Cho điểm O nằm giữa hai điểm A và B. Gọi M và N theo thứ tự là trung điểm của OA và OB. Tính độ dài MN, biết AB = a
Bài 8: Cho đoạn thẳng AB= 6cm. Lấy điểm C thuộc đoạn thẳng AB sao cho AC=4cm. Gọi M và N lần lượt là trung điểm của các đoạn thẳng AC và BC.
a) Tính độ dài MC và NC.
b) Chứng tỏ điểm C nằm giữa hai điểm M và N.
c) Tính độ dài MN.