Tính bằng cách thuận tiện nhất là một dạng toán thường gặp ở cấp tiểu học, nhất là trong phần dạng bài tính giá trị biểu thức phức tạp trong chương trình toán lớp 4. Mời các bạn cùng tham khảo bài viết dưới đây.
Mục lục bài viết
1. Cách tính và mẹo tính bằng cách thuận tiện nhất:
Cách 1: Nhóm/tách các số trong biểu thức thành từng nhóm có tổng (hoặc hiệu) là các số tròn chục, tròn trăm, tròn nghìn, hoặc để xuất hiện nhân số chung
Ví dụ : Tính bằng cách thuận tiện nhất
A = 189 + 555 + 211 + 45 = (189 + 211) + (555 + 45) = 400 + 600 = 1000.
B = 1587 + 2550 – 187 = (1587 – 187) + 2550 = 1400 + 2550 = 3950.
C = 25 + 46 + 23 + 75 + 77 + 54 = (25 + 75) + (46 + 54) + (23 + 77) = 100 + 100 + 100 = 300
D = 31 + 52 + 33 + 24 + 45 + 26 + 17 + 48 + 19 = (31 + 19) + (52 + 48) + (33 + 17) + (24 + 26) + 45 = 50 + 100 + 50 + 50 + 45 = 250 + 45 = 295
Cách 2: Phép cộng các số giống nhau được biểu diễn bằng phép nhân
Ví dụ:
a) 7 + 7 + 7 + 7+ 7 + 7 +7+ 7 + 7 +7 = 7 x 10 = 70
b) 25 + 25 + 25 + 25 + 25 + 25 +25 + 25 = 25 x 8 = 200
Cách 3: Vận dụng các tính chất của phép cộng, phép nhân, phép trừ, phép chia
+ Nhân một số với một tổng: a x (b + c) = a x b + a x c
Ví dụ : 123 x 10 + 137 x 10 = 10 x (123 + 137) = 10 x 260 = 2600
+ Nhân một số với một hiệu: a x (b – c) = a x b – a x c
Ví dụ : 450 x 20 – 120 x 20 = 20 x (450 – 120) = 20 x 330 = 6600
+ Một tổng chia cho một số: (a + b) : c = a : c + b : c
Ví dụ : 240 : 12 + 360 : 12 = (240 + 360) : 12 = 600 : 12 = 50
+ Một số trừ đi một tổng: a – (b + c) = a – b – c
Ví dụ : 467 – ( 167 + 50) = 467 – 167 – 50 = 300 – 50 = 250.
Cách 4: Vận dụng các tính chất với các số đặc biệt
+ 0 nhân với một số: 0 x a = a x 0 = 0
+ 0 chia cho một số: 0 : a = 0
+ 1 nhân với một số: 1 x a = a x 1 = a
+ Chia một số cho 1: a : 1 = a
Ví dụ:
A = 897 x 548 x (246 – 123 x 2) = 897 x 548 x (246 – 246) = 897 x 548 x 0 = 0
B = (540 – 240) x ( 127 – 42 x 3) = 300 x (127 – 126) = 300 x 1 = 300
C = 199 : (489 – 122 x 4) = 199 : (489 – 488) = 199 : 1 = 199
D = 123 x 456 x (450 – 225 x 2) = 123 x 456 x (450 – 450) = 123 x 456 x 0 = 0
Quy tắc 5: Tính thuận tiện với biểu thức có phân số
Kết hợp các thao tác sau:
– Nhóm các phân số trong biểu thức thành từng nhóm có tổng (hoặc hiệu) bằng 1 hoặc 0.
– Vận dụng tính chất của 4 phép tính để tách hoặc ghép ở tử số hoặc ở mẫu số để tạo ra thừa số giống nhau ở cả mẫu số và tử số rồi thực hiện rút gọn biểu thức.
– Phép cộng các số giống nhau được biểu diễn bằng phép nhân
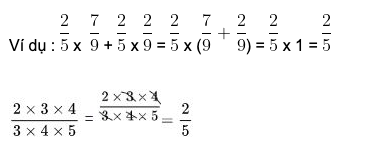
2. Một số bài tập tính bằng cách thuận tiện nhất:
Bài 1 : Tính bằng cách thuận tiện nhất các biểu thức sau :
A = 25 x 16 x 4 x 5
B = 137 x 92 + 137 x 8
C = 56 x 89 – 46 x 89
D = 4550 – 4 x 155 – 6 x 155
E = 5231 – 2 x 456 + 2 x 156
Bài 2: Tính bằng cách thuận tiện nhất các biểu thức dưới đây
A = 25 x 15 x 4 x 6
B = 124 x 92 + 124 x 8
C = 76 x 52 – 66 x 52
D = 4550 – 4 x 155 – 6 x 155
E = 231 – 2 x 122 + 2 x 22
Bài 3: Tính bằng cách thuận tiện nhất :
a) 456 + 675 + 244 – 375
b) 2667 + 590 – 567 + 310
c) 1789 x 5467 x (460 – 230 x 2)
d) 700 + 197 – 200 + 203
e) (237 + 113) : (419 – 209 x 2)
Bài 4: Tính bằng cách thuận tiện nhất các biểu thức sau
a) 556 + 670 + 444 – 270
b) 2632 + 527 – 532 + 373
c) 1425 x 5890 x (250 – 125 x 2)
d) 700 + 197 – 200 + 203
e) (237 + 113) : (419 – 209 x 2)
Bài 5: Tính bằng cách thuận tiện nhất :
A = 11/20 x 5/8 + 3/8 x 11/20
B = 2/9 : 6/7 + 7/9 x 7/6
C = 5/6 + 1/4 – 2/6 + 7/4
D = 7/3 – 20/21 + 13/21 – 2/3
Bài 6: Tính bằng cách thuận tiện nhất :
A = 46 x 17 + 38 x 46 + 46 x 44 + 46
B = 125 x 25 + 25 x 874 + 25
C = 47 x 105 – 6 x 47 + 47
D = 52 x 315 + 48 x 315
E = 422 x 19 + 422 x 77 + 422 x 4
Bài 7: Tính bằng cách thuận tiện nhất :
A = 0,12 X 400
B = 0,25 x 1,25 x 4 x 8
C = 8,3 x 7,9 + 7,9 x 1,7
D = 32,5 x 6,5 + 3,5 x 32,5
E = 9,9 x 5 x 0,2
3. Đáp án bài tập tính bằng cách thuận tiện nhất:
Bài 1 :
A = 25 x 16 x 4 x 5 = 25 x 4 x 16 x 5 = 100 x 80 = 8000
B = 137 x 92 + 137 x 8 = 137 x (92 + 8) = 137 x 100 = 13700
C = 56 x 89 – 46 x 89 = (56 – 46) x 89 = 10 x 89 = 890
D = 4550 – 4 x 155 – 6 x 155 = 4550 – (4 + 6) x 155 = 4550 – 10 x 155 = 4550 – 1550 = 3000
E = 5231 – 2 x 456 + 2 x 156 = 5231 – 2 x (456 – 156) = 5231 – 2 x 300 = 5231 – 600 = 4631
Bài 2:
A = 25 x 15 x 4 x 6 = 25 x 4 x 15 x 6 = 100 x 90 = 9000
B = 124 x 92 + 124 x 8 = 124 x (92 + 8) = 124 x 100 = 12400
C = 76 x 52 – 66 x 52 = (76 – 66) x 52 = 10 x 52 = 520
D = 4550 – 4 x 155 – 6 x 155 = 4550 – (4 + 6) x 155 = 4550 – 10 x 155 = 4550 – 1550 = 3000
E = 231 – 2 x 122 + 2 x 22 = 231 – 2 x (122 – 22) = 231 – 2 x 100 = 231 – 200 = 31
Bài 3:
a) 456 + 675 + 244 – 375 = (456 + 244) + (675 – 375) = 700 + 300 = 1000
b) 2667 + 590 – 567 + 310 = (2667 – 567) + (590 + 310) = 2100 + 900 = 3000
c) 1789 x 5467 x (460 – 230 x 2) = 1789 x 5467 x (460 – 460) = 1789 x 5467 x 0 = 0
d) 700 + 197 – 200 + 203 = 700 – 200 + (197 + 203) = 500 + 400 = 900
e) (237 + 113) : ( 419 – 209 x 2) = 450 : (419 – 418) = 450 : 1 = 450
Bài 4:
a) 556 + 670 + 444 – 270 = (556 + 444) + (670 – 270) = 1000 + 400 = 1400
b) 2632 + 527 – 532 + 373 = (2632 – 532) + (527 + 373) = 2100 + 900 = 3000
c) 1425 x 5890 x (250 – 125 x 2) = 1425 x 5890 x (250 – 250) = 1425 x 5890 x 0 = 0
d) 700 + 197 – 200 + 203 = 700 – 200 + (197 + 203) = 500 + 400 = 900
e) (237 + 113) : ( 419 – 209 x 2) = 450 : (419 – 418) = 450 : 1 = 450
Bài 5:
A = 11/20 x 5/8 + 3/8 x 11/20 = 11/20 x (5/8 + 3/8) = 11/20 x 1 = 11/20
B = 2/9 : 6/7 + 7/9 : 6/7 = (2/9 + 7/9) : 6/7 = 1 : 6/7 = 7/6
C = 5/6 + 1/4 – 2/6 + 7/4 = (5/6 – 2/6) + (1/4 + 7/4) = 1/2 + 2 = 5/2
D = 7/3 – 20/21 + 13/21 – 2/3 = (7/3 – 2/3) – (20/21 – 13/21) = 5/3 – 1/3 = 4/3
Bài 6:
A = 46 x 17 + 38 x 46 + 46 x 44 + 46 = 46 x (17 + 38 + 44 + 1) = 46 x 100 = 4600
B = 125 x 25 + 25 x 874 + 25 = 25 x (125 + 874 + 1) = 25 x 1000 = 25000
C = 47 x 105 – 6 x 47 + 47 = 47 x (105 – 6 + 1) = 47 x 100 = 4700
D = 52 x 315 + 48 x 315 = 315 x (52 + 48) = 315 x 100 = 31500
E = 422 x 19 + 422 x 77 + 422 x 4 = 422 x (19 + 77 + 4) = 422 x 100 = 42200
Bài 7:
A = 0,12 x 400 = 0,12 x 100 x 4 = 12 x 4 = 48
B = 0,25 x 1,25 x 4 x 8 = 0,25 x 4 x 1,25 x 8 = 1 x 10 = 10
C = 8,3 x 7,9 + 7,9 x 1,7 = 7,9 x (8,3 + 1,7) = 7,9 x 10 = 79
D = 32,5 x 6,5 + 3,5 x 32,5 = 32,5 x (6,5 + 3,5) = 32,5 x 10 = 325
E = 9,9 x 5 x 0,2 = 9,9 x 1 = 9,9




