Bài tập Tìm m để bất phương trình có nghiệm | Toán 10

1. Lý thuyết bài tập Tìm m để bất phương trình có nghiệm:

Để bất phương trình có nghiệm, ta cần điều kiện để hàm số đổi dấu. Ta xét các trường hợp sau:

– Nếu m < 0, ta có hàm số luôn âm với mọi x. Vậy bất phương trình vô nghiệm.

– Nếu m = 0, ta có hàm số bằng 0 với mọi x. Vậy bất phương trình vô nghiệm.

– Nếu m > 0, ta có hàm số có hai nghiệm phân biệt x1 và x2 (x1 < x2) là các nghiệm của phương trình bậc hai. Khi đó, hàm số đổi dấu tại x1 và x2. Vậy bất phương trình có nghiệm khi và chỉ khi x < x1 hoặc x > x2.

Để tìm m, ta cần giải phương trình bậc hai và tìm điều kiện để có hai nghiệm phân biệt. Ta có:

mx^2 + (2 – m)x – 3 = 0

Δ = (2 – m)^2 + 12m = m^2 + 4m + 4

Để có hai nghiệm phân biệt, ta cần Δ > 0, tức là:

m^2 + 4m + 4 > 0

Ta nhận thấy đây là một tam thức luôn dương với mọi m. Vậy điều kiện trên luôn thỏa mãn.

Từ đó, ta suy ra m > 0 là điều kiện cần và đủ để bất phương trình có nghiệm.

Tóm tắt lại các bước như sau: Giải phương trình bậc hai mx^2 + (2 – m)x – 3 = 0 và tìm điều kiện để có hai nghiệm phân biệt, sau đó xét dấu của hàm số để tìm khoảng nghiệm của bất phương trình. Kết quả là m > 0.

2. Bài tập tìm m để bất phương trình có nghiệm và lời giải chi tiết:

Bài 1: Tìm m để bất phương trình |x – 2| + |x – m| > 3 có nghiệm.

Lời giải:

Ta có hai trường hợp:

– Trường hợp 1: x – 2 < 0 và x – m < 0

Khi đó, bất phương trình trở thành -(x – 2) – (x – m) > 3

Tương đương với 2x < m + 1

– Trường hợp 2: x – 2 > 0 và x – m > 0

Khi đó, bất phương trình trở thành (x – 2) + (x – m) > 3

Tương đương với 2x > m + 5

Vậy, để bất phương trình có nghiệm, ta cần có m + 1 < m + 5

Tức là m > -4

Đáp số: m > -4

Bài 2: Tìm m để bất phương trình mx^2 – (m+1)x + 1 > 0 có nghiệm.

Lời giải: Để bất phương trình có nghiệm, ta cần điều kiện: 

– Hệ số a = m khác 0

– Định thức D = (m+1)^2 – 4m > 0

Giải hệ này, ta được: m < -1/2 hoặc m > 1

Bài 3: Tìm m để bất phương trình (m-1)x^2 + (2m-3)x + m < 0 có nghiệm.

Lời giải: Để bất phương trình có nghiệm, ta cần điều kiện:

– Hệ số a = m-1 khác 0

– Định thức D = (2m-3)^2 – 4(m-1)m > 0

Giải hệ này, ta được: m < -1 hoặc 0 < m < 3/4

Bài 4: Tìm m để phương trình  có nghiệm.

Giải

– Nếu m < 2 –> phương trình vô nghiệm.

– Nếu m ≥ 2 –> phương trình <–> x2−2mx−m2+4m−3=0. Phương trình này có Δ=2m2−4m+3>0 với mọi m.

Vậy với m ≥ 2 thì phương trình đã cho có nghiêm.

Bài 5: Tìm m để phương trình  có hai nghiệm phân biệt.

Giải: 

Cách 1: 

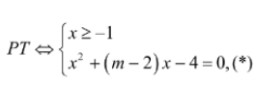, phương trình (*) luôn có 2 nghiệm: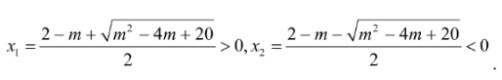

Phương trình đã cho có 2 nghiệm <–>(*) có 2 nghiệm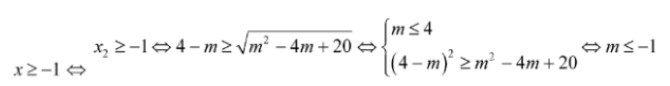

Chú ý: + x1 > 0, x2 < 0 vì x1 > x2 và a.c < 0 nên pt có 2 nghiệm trái dấu.

– Cách 1 thường dùng khi hệ số a luôn dương hoặc luôn âm.

– Cách 2: Đặt t = x + 1 suy ra x = t – 1, khi đó với

(*) trở thành: (**). Để (*) có 2 nghiệm   thì (**) phải có 2 nghiệm .

Bài 6: Tìm m để phương trình có hai nghiệm thực phân biệt: , (1)

Giải: 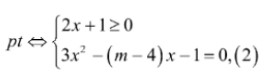để (1) có hai nghiệm thực phân biệt thì (2) có hai nghiệm lớn hơn hoặc bằng -1/2 hay .

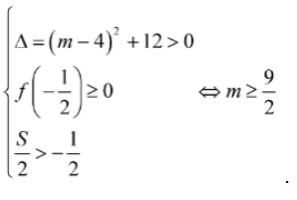Chú ý: Cách 2: đặt , khi đó để (2) có hai nghiệm lớn hơn hoặc bằng 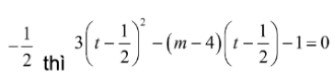 có hai nghiệm thực lớn hơn hoặc bằng 0.

Bài 7: Tìm m để phương trình sau có nghiệm: .

Giải

Đặt: .

Khi đó phương trình trở thành .

Phương trình đã cho có nghiệm khi (*) có nghiệm hay .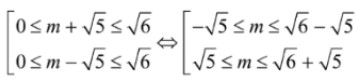

Bài 8: Tìm m để bất phương trình: , (1) có nghiệm .

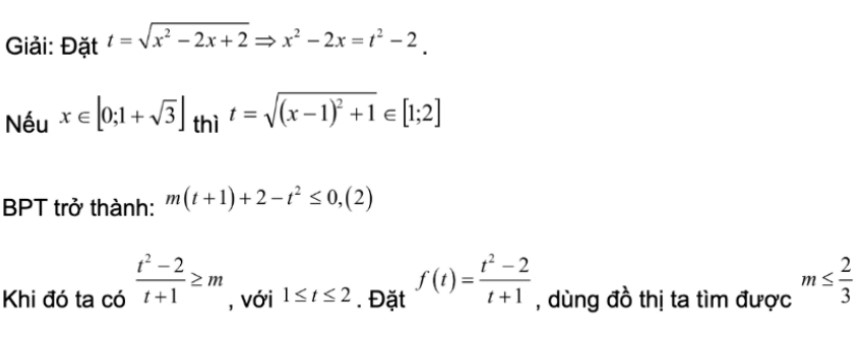
Bài 9: Cho phương trình .

a. Giải phương trình khi m=3.

b. Tìm m để phương trình đã cho có nghiệm.

Giải

Đặt: .

Áp dụng bất đẳng thức Cauchy nên từ (*) ta có

Phương trình đã cho trở thành t2−2t−9=−2m (1).

a. Với m=3 (1) ⇔ t2−2t−3 ⇔ t =3.

Thay vào (*) ta được x=−3, x=6.

b. PT đã cho có nghiệm khi và chỉ khi (1) có nghiệm .

Xét hàm số  , ta thấy f(t) là một hàm đb nên:  

Do vậy (1) có nghiệm khi và chỉ khi

Bài 10: Tìm m để phương trình sau có nghiệm: .

Giải:

ĐK

Xét hai trường hợp x = 1 và x ≠ 1, C

hia hai vế phương trình cho .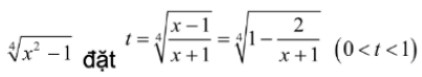

ĐS .

Bài 11: Tìm m để phương trình:  có nghiệm.

TXĐ: R

Xét hs: , Df = R,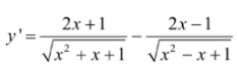

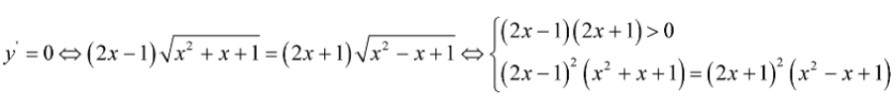(v.nghiệm)

Mặt khác: f’(0) = 1 > 0 suy ra y’ > 0 nên hàm số đồng biến.

Giới hạn: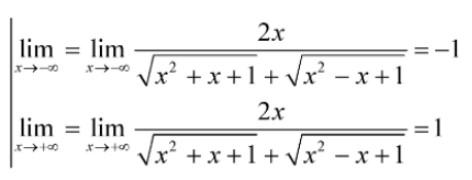

Vậy phương trình có nghiệm khi và chỉ khi −1 < m < 1.

Chú ý: Trong bài toán trên nếu không thực hiện việc xác định giới hạn hàm số, rất có thể chúng ta ngộ nhận tập giá trị của hàm số là R và dẩn đến việc kết luận sai lầm rằng phương trình có nghiệm với mọi m. Do đó việc tìm giới hạn trong bài toán khảo sát là rất cần thiết để tìm ra tập giá trị.

Bài 12:  Tìm m để bất phương trình sau có nghiệm:

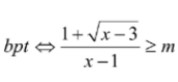, xét hs  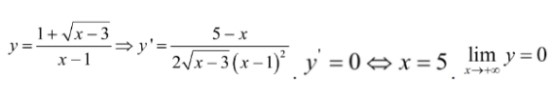 và f(3) = 1/

Vậy bất phương trình có nghiệm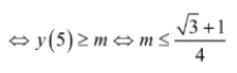

Bài 13:  Tìm m để phương trình: 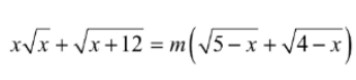 có nghiệm.

Giải: ĐK:

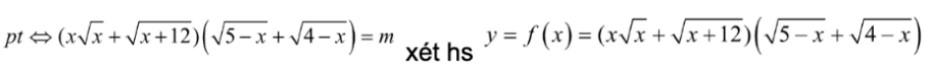
Miền xác định:

Nhận xét: Hàm số  đồng biến trên D.

Hàm số  đồng biến trên D.

Suy  ra y = f(x) = h(x).g(x) là hàm đồng biến trên D.

Vậy phương trình có nghiệm khi và chỉ khi

Bài 14:  Tìm m để phương trình sau có nghiệm: , (1)

Khi đó phương trình (1) trở thành: -1/2 t2 + t + 1 = m, lập bảng biến thiên của hàm số vế trái với

3. Một số lưu ý với bài tập tìm m để bất phương trình có nghiệm:

Để tìm m để bất phương trình có nghiệm, ta cần xét các trường hợp của hệ số a, b, c của đa thức bậc hai ax^2 + bx + c. Ta có ba trường hợp chính:

– Nếu a = 0, ta có bất phương trình bậc nhất bx + c > 0. Ta giải bất phương trình này bằng cách chia hai vế cho b (nếu b khác 0) và đảo dấu nếu b < 0. Ta được nghiệm là x > -c/b (nếu b > 0) hoặc x < -c/b (nếu b < 0). Nếu b = 0, ta có c > 0 là điều kiện cần và đủ để bất phương trình có nghiệm.

– Nếu a khác 0, ta có bất phương trình bậc hai ax^2 + bx + c > 0. Ta tìm nghiệm của phương trình ax^2 + bx + c = 0 bằng công thức nghiệm của phương trình bậc hai: x1, x2 = (-b ± √(b^2 – 4ac))/(2a). Ta có ba trường hợp con:

+ Nếu ∆ = b^2 – 4ac < 0, phương trình vô nghiệm. Khi đó, đồ thị của hàm số y = ax^2 + bx + c không cắt trục hoành. Ta xét dấu của a để xác định dấu của y. Nếu a > 0, y luôn dương và bất phương trình có nghiệm là R (tập hợp các số thực). Nếu a < 0, y luôn âm và bất phương trình vô nghiệm.

+ Nếu ∆ = 0, phương trình có nghiệm kép x1 = x2 = -b/(2a). Khi đó, đồ thị của hàm số y = ax^2 + bx + c tiếp xúc với trục hoành tại điểm có hoành độ là -b/(2a). Ta xét dấu của a để xác định dấu của y. Nếu a > 0, y dương khi x khác -b/(2a) và bất phương trình có nghiệm là R {-b/(2a)}. Nếu a < 0, y âm khi x khác -b/(2a) và bất phương trình vô nghiệm.

+ Nếu ∆ > 0, phương trình có hai nghiệm phân biệt x1 < x2. Khi đó, đồ thị của hàm số y = ax^2 + bx + c cắt trục hoành tại hai điểm có hoành độ là x1 và x2. Ta xét dấu của a để xác định dấu của y. Nếu a > 0, y dương khi x < x1 hoặc x > x2 và bất phương trình có nghiệm là (-∞; x1) ∪ (x2; +∞). Nếu a < 0, y âm khi x1 < x < x2 và bất phương trình vô nghiệm.

Từ các trường hợp trên, ta có thể tìm được m để bất phương trình có nghiệm dựa vào các giá trị của a, b, c.