Đường trung tuyến là khái niệm quan trọng trong hình học và được nhiều học sinh quan tâm trong môn Toán. Dưới đây là bài viết về chủ đề: Đường trung tuyến là gì? Tính chất đường trung tuyến?, mời bạn đọc theo dõi.
Mục lục bài viết
1. Đường trung tuyến là gì?
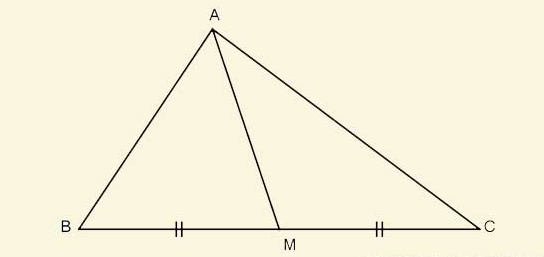
Đường trung tuyến là một khái niệm trong hình học, nó là một đoạn thẳng đi qua trung điểm của một đoạn thẳng hay nối từ đỉnh của một tam giác đến trung điểm của cạnh đối diện.
Trước tiên, để hiểu rõ hơn về đường trung tuyến, chúng ta cần biết khái niệm “trung điểm.” Trung điểm là điểm nằm ở giữa của một đoạn thẳng và cách hai đầu của đoạn thẳng bằng nhau. Để tìm trung điểm của một đoạn thẳng, ta chỉ cần nối hai đầu của đoạn thẳng bằng một đoạn thẳng khác và điểm giao nhau của hai đoạn thẳng chính là trung điểm của đoạn thẳng ban đầu.
Vậy đường trung tuyến là gì? Đường trung tuyến của một đoạn thẳng là một đường thẳng đi qua trung điểm của đoạn thẳng đó. Nó chia đoạn thẳng ban đầu thành hai đoạn có chiều dài bằng nhau.
Trong tam giác, đường trung tuyến có ý nghĩa quan trọng. Đối với mỗi tam giác, ta có ba đường trung tuyến, mỗi đường trung tuyến nối từ đỉnh của tam giác đến trung điểm của cạnh đối diện. Ba đường trung tuyến này cắt nhau tại một điểm gọi là trọng tâm của tam giác. Trọng tâm là điểm duy nhất trong tam giác mà ba đường trung tuyến đều cắt nhau và chia đôi nhau thành bốn đoạn thẳng có cùng độ dài.
Trong tổng quát, đường trung tuyến là một khái niệm hữu ích trong hình học và tam giác, nó giúp chúng ta hiểu rõ hơn về sự đối xứng và phân chia của các đoạn thẳng trong hình học học.

2. Tính chất đường trung tuyến:
Tính chất của đường trung tuyến trong tam giác là một khái niệm hình học quan trọng và có nhiều điểm đáng chú ý.
– Tính chất đường trung tuyến trong tam giác thường:
Tam giác thường có ba đoạn đường trung tuyến, mỗi đoạn nối từ một đỉnh của tam giác đến trung điểm của cạnh đối diện. Ba đoạn đường trung tuyến này cắt nhau tại một điểm, và điểm đó là trọng tâm của tam giác. Trọng tâm là điểm duy nhất mà ba đoạn đường trung tuyến cắt nhau và chia đoạn trung tuyến từ trọng tâm đến các đỉnh của tam giác theo tỷ lệ 2:1. Trọng tâm có tính chất đặc biệt, khi mà nếu ta nối trọng tâm với các đỉnh của tam giác, các đoạn đường này có thể gọi là đoạn đồng giác và nằm trong tam giác đó.
– Tính chất đường trung tuyến trong tam giác vuông:
Trong tam giác vuông, đường trung tuyến đi qua trung điểm của cạnh huyền sẽ có độ dài bằng một nửa cạnh huyền. Điều này có thể dễ dàng kiểm chứng bằng cách chia tam giác vuông thành hai tam giác nhỏ bằng nhau. Đường trung tuyến trong tam giác vuông cũng cắt nhau tại trọng tâm của tam giác và tạo thành bốn đoạn đồng giác có cùng độ dài.
Giả sử: Tam giác ABC vuông có cạnh AD là trung tuyến ứng với cạnh huyền BC.
=> AD = 1/2BC = DB = DC
Ngược lại, nếu trung tuyến AD = 1/2BC thì ABC vuông tại đỉnh A.
– Tính chất đường trung tuyến trong tam giác cân:
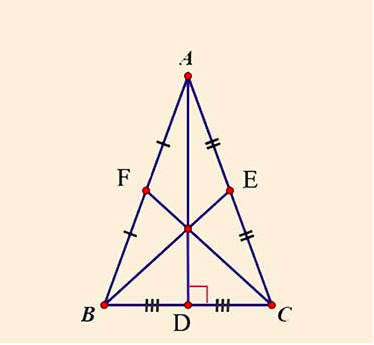
Giả sử: Tam giác ABC cân tại đỉnh A, có đường trung tuyến AD ứng với cạnh đáy BC.
Suy ra:
AD vuông góc với cạnh BC
ΔADB = ΔADC
Trong tam giác cân, đường trung tuyến từ đỉnh đến cạnh đáy là đoạn thẳng vuông góc với cạnh đáy và chia tam giác thành hai tam giác nhỏ bằng nhau. Điều này có thể chứng minh bằng cách nối đỉnh của tam giác cân đến các điểm trung điểm của các cạnh đối diện. Đường trung tuyến cắt nhau tại trọng tâm của tam giác cân và tạo thành bốn đoạn đồng giác có độ dài bằng nhau.
– Tính chất đường trung tuyến trong tam giác:
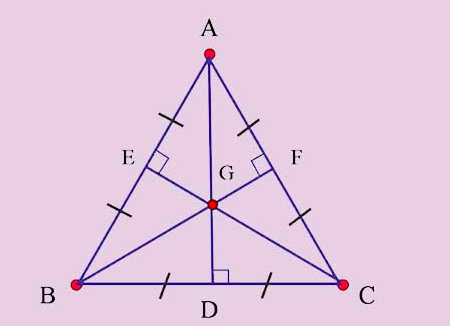
Giả sử: Tam giác ΔABC đều. Trung điểm của các cạnh BC, AB và AC lần lượt là các điểm D, E, F. Điểm G là trọng tâm của tam giác đều ABC.
Suy ra:
ΔGAE = ΔGCF = ΔGAF = ΔGCD = ΔGBE = ΔGBD = ΔGEB = ΔGEA
SADB = SADC = SCEA = SCEB = SBFA = SBFC
Trong tam giác đều, có ba đoạn đường trung tuyến, mỗi đoạn nối từ một đỉnh của tam giác đến trung điểm của cạnh đối diện. Ba đoạn đường trung tuyến này có những tính chất đặc biệt và thú vị:
+ Chia tam giác thành 6 tam giác con có diện tích bằng nhau: Đầu tiên, ba đoạn đường trung tuyến của tam giác đều sẽ chia tam giác thành 6 tam giác con. Điểm đặc biệt là các tam giác con này có diện tích bằng nhau. Điều này có nghĩa là tổng diện tích của bất kỳ bốn tam giác con nào trong số sáu tam giác con trên đều bằng diện tích của hai tam giác con còn lại.
+ Trung tâm là điểm chung của 3 đoạn đường trung tuyến: Một điểm đặc biệt trong tam giác đều là trung tâm G, là điểm giao nhau của ba đoạn đường trung tuyến. Trung tâm này có một số tính chất đáng chú ý. Khoảng cách từ trung tâm G đến một đỉnh bất kỳ của tam giác đều bằng 2/3 chiều dài đoạn đường trung tuyến từ G đến đỉnh đó.
+ Đối xứng và đồng giác: Đường trung tuyến trong tam giác đều đồng giác với các cạnh của tam giác và chia chúng thành hai phần bằng nhau. Điều này tạo ra các đoạn đồng giác trong tam giác đều có cùng độ dài. Ngoài ra, khi nối trung tâm G với các đỉnh của tam giác, ta cũng thu được các đoạn đồng giác có cùng độ dài, và chúng tạo thành một đa giác đều.
Trong trường hợp cụ thể, nếu ta xét tam giác đều ΔABC, và trung điểm của các cạnh BC, AB, và AC lần lượt là D, E, F, thì trung tâm G của tam giác này sẽ chia tam giác thành 6 tam giác con có diện tích bằng nhau, và các tam giác con này sẽ đồng dạng với nhau. Khi nối trung tâm G với các đỉnh của tam giác, ta thu được một đa giác đều có các đoạn đồng giác cùng độ dài.
Những tính chất này giúp chúng ta hiểu rõ hơn về sự tương quan giữa các đoạn thẳng và điểm trong tam giác. Chúng ta có thể sử dụng các tính chất này để giải quyết các bài toán hình học liên quan đến tam giác một cách hiệu quả và chính xác.
3. Công thức tính độ dài đường trung tuyến của tam giác:
Để tính độ dài đường trung tuyến trong tam giác, chúng ta có thể sử dụng định lý Apollonnius, một công thức quan trọng trong hình học tam giác. Định lý Apollonnius cho phép tính độ dài của đoạn đường trung tuyến dựa trên các đoạn cạnh của tam giác.
Giả sử tam giác ABC có ba cạnh lần lượt là a, b, và c. Đường trung tuyến từ đỉnh A đến trung điểm của cạnh đối diện BC có độ dài là m. Công thức tính độ dài đường trung tuyến AM (trong đó M là trung điểm của BC) theo định lý Apollonnius là:
m^2 = (b^2 + c^2)/2 – (a^2)/4
Tương tự, ta có thể tính độ dài của đường trung tuyến BN và đường trung tuyến CP từ đỉnh B và C đến trung điểm của các cạnh đối diện AC và AB bằng cách thay đổi vị trí của các cạnh trong công thức trên.
Lưu ý rằng định lý Apollonnius chỉ áp dụng cho tam giác có điểm trung điểm và điểm trọng tâm. Nếu ta không biết thông tin về trung điểm và trọng tâm của tam giác, thì không thể áp dụng công thức này. Để tính độ dài đường trung tuyến mà không cần biết thông tin về trung điểm và trọng tâm, ta cần sử dụng các phương pháp khác như sử dụng hệ thức hình học và tính toán góc và cạnh của tam giác.
4. Dạng bài tập đường trung tuyến của tam giác:
Các bài tập về đường trung tuyến trong tam giác có thể được phân thành một số dạng khác nhau, tùy thuộc vào yêu cầu cụ thể của đề bài. Dưới đây là một số dạng bài tập thường gặp về đường trung tuyến trong tam giác và phương pháp giải tương ứng:
Dạng 1: Sử dụng tính chất trọng tâm của tam giác
Phương pháp giải:
Bước 1: Vẽ tam giác và xác định các đỉnh A, B, C.
Bước 2: Tìm trung điểm của các cạnh tam giác để xác định các đoạn đường trung tuyến AD, BE, CF.
Bước 3: Xác định trọng tâm G của tam giác, là điểm giao nhau của ba đoạn đường trung tuyến. Ta có thể tính toán các tọa độ của G bằng cách lấy trung bình cộng tọa độ các đỉnh tam giác.
Bước 4: Kiểm tra tính đồng quy của ba đoạn đường trung tuyến, nếu chúng cùng giao nhau tại trọng tâm G thì đúng tính chất trọng tâm của tam giác.
Dạng 2: Chứng minh một điểm là trọng tâm tam giác
Phương pháp giải:
Bước 1: Xác định tam giác ABC và một điểm M bất kỳ trong tam giác.
Bước 2: Tìm độ dài các đoạn đường trung tuyến AM, BM, CM từ điểm M đến các trung điểm của các cạnh tương ứng.
Bước 3: Nếu các đoạn đường trung tuyến AM, BM, CM cắt nhau tại một điểm G và độ dài của các đoạn đường trung tuyến AM, BM, CM là 2/3 độ dài các cạnh tương ứng, thì ta chứng minh được rằng điểm M là trọng tâm của tam giác ABC.
Dạng 3: Đường trung tuyến của tam giác cân, tam giác đều, tam giác vuông
Phương pháp giải:
Bước 1: Xác định tam giác và các thông tin về loại tam giác (cân, đều, vuông).
Bước 2: Áp dụng các tính chất đặc biệt của tam giác cân, tam giác đều và tam giác vuông để tính độ dài đường trung tuyến một cách chính xác. Ví dụ: Đối với tam giác vuông, đoạn đường trung tuyến đi qua trung điểm của cạnh huyền có độ dài bằng một nửa của cạnh huyền.
Các dạng bài tập về đường trung tuyến trong tam giác đòi hỏi chúng ta nắm vững tính chất và công thức liên quan đến trọng tâm và đường trung tuyến của tam giác để giải quyết một cách chính xác và hiệu quả.
5. Bài tập đường trung tuyến của tam giác:
Bài 1: Cho tam giác ABC có đường trung tuyến AD = 9cm và trọng tâm I. Tính độ dài của đoạn AI?
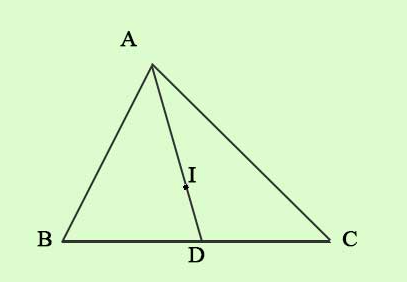
Hình minh họa bài tập 1
Lời giải:
Ta có: – Điểm I là trọng tâm của tam giác ABC.
– AD là đường trung tuyến.
=> AI = (2/3) AD (theo tính chất ba đường trung tuyến của tam giác ở bên trên).
Do đó: AG = (2/3).9 = 6 (cm).
Vậy đọan AI cần tìm có độ dài 6 cm.
Bài 2:
Cho điểm I là trọng tâm của tam giác đều MNP. Hãy chứng minh rằng: IM = IN = IP.
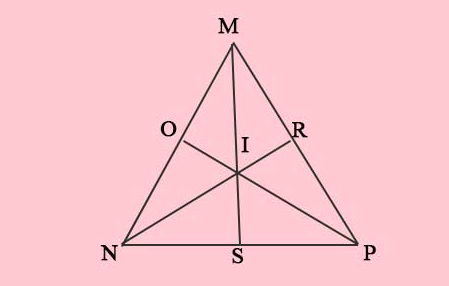
Hình minh họa bài tập 2
Lời giải:
Gọi trung điểm của các cạnh MN, MP và PN lần lượt là R, O, S. Khi đó, các đường trung tuyến MS, PR, NO sẽ đồng quy tại trọng tâm I.
Ta có tam giác MNP đều, suy ra:
MS = PR = NO (1).
Vì I là trọng tâm của tam giác MNP nên theo tính chất của đường trung tuyến ta có:
MI = 2/3 MS, PI = 2/3 PR và NI = 2/3 NO (2).
Từ (1) và (2) ⇒ IM = IN = IP.




