Mục lục bài viết
1. Phương pháp giải nhanh bất phương trình bậc 2 dễ hiểu:
Cách giải các hệ bất phương trình bậc hai điển hình như sau:
Bước 1: Xác định biểu thức của các bất phương trình trong hệ. Định rõ biểu thức và điều kiện của từng bất phương trình để có thể xử lý tiếp theo.
Ví dụ: Giả sử hệ gồm hai bất phương trình là:
2x^2 + 9x + 7 > 0
x^2 + x – 6 < 0
Bước 2: Giải từng bất phương trình độc lập. Để giải một bất phương trình bậc hai, ta thực hiện các bước sau:
2a. Xác định hệ số a, b và c của bất phương trình. Trong trường hợp này, a = 2, b = 9 và c = 7.
2b. Xác định delta (Δ) bằng công thức Δ = b^2 – 4ac.
2c. Kiểm tra giá trị của delta (Δ) để xác định tính chất của nghiệm:
– Nếu Δ > 0, bất phương trình có hai nghiệm phân biệt.
– Nếu Δ = 0, bất phương trình có một nghiệm kép.
– Nếu Δ < 0, bất phương trình không có nghiệm thực.
Trong trường hợp này, ta tính delta của bất phương trình thứ nhất:
Δ1 = (9)^2 – 4(2)(7) = 81 – 56 = 25
Vì Δ1 > 0 nên bất phương trình thứ nhất có hai nghiệm phân biệt.
2d. Tính toán nghiệm bằng cách sử dụng công thức: x = (-b ± √Δ) / 2a
Dựa trên kết quả tính toán, ta có thể xác định nghiệm của bất phương trình thứ nhất.
Bước 3: Xác định nghiệm chung của hệ:
– Nếu giá trị của biến nằm trong khoảng giữa hai nghiệm của từng bất phương trình đồng thời, thì giá trị đó là nghiệm chung.
– Nếu không có khoảng nào chứa cả hai nghiệm của từng bất phương trình, thì hệ không có nghiệm chung.
Tiếp tục giải bất phương trình thứ hai và áp dụng các bước tương tự để tìm nghiệm của bất phương trình này.
Sau khi tìm được nghiệm của cả hai bất phương trình, ta kiểm tra khoảng nghiệm chung để xác định nghiệm chung của hệ.
Lưu ý: Cách giải này chỉ áp dụng cho hệ bất phương trình bậc hai. Các trường hợp khác có thể có cách giải riêng biệt tương ứng.
2. Lưu ý cần nhớ khi giải hệ bất phương trình bậc hai:
Khi giải hệ bất phương trình bậc hai, chúng ta cần nhớ những điểm quan trọng sau:
1. Xác định đúng số lượng nghiệm của hệ bất phương trình bậc hai, tức là hệ có thể có 0, 1 hoặc nhiều nghiệm. Điều này phụ thuộc vào số lượng phương trình và sự liên hệ giữa chúng.
2. Đối với từng phương trình trong hệ, chúng ta cần giải riêng và tìm nghiệm của mỗi phương trình.
3. Khi giải phương trình bậc hai, chúng ta sẽ sử dụng công thức nghiệm phổ biến là công thức Vi-et:
Xét phương trình ax^2 + bx + c = 0. Ta có:
Delta = b^2 – 4ac
Nếu Delta > 0, thì phương trình có hai nghiệm phân biệt: x1 = (-b + sqrt(Delta))/(2a) và x2 = (-b – sqrt(Delta))/(2a).
Nếu Delta = 0, thì phương trình có nghiệm kép: x = -b/(2a).
Nếu Delta < 0, thì phương trình không có nghiệm thực.
4. Sau khi tìm ra các nghiệm của từng phương trình, chúng ta cần kiểm tra xem các nghiệm đó có thỏa mãn tất cả các phương trình trong hệ bất phương trình hay không. Điều này phụ thuộc vào sự liên hệ và điều kiện giữa từng phương trình.
5. Cuối cùng, chúng ta cần kết hợp các kết quả và tìm ra tất cả các nghiệm của hệ bất phương trình bậc hai.
3. Giải bài tập bất phương trình bậc 2:
Dạng 1: Xét dấu của tam thức bậc 2
Bài 1 trang 105 SGK Đại Số 10: Xét dấu các tam thức bậc hai:
a) 5x2 – 3x + 1
b) -2x2 + 3x + 5
c) x2 + 12x + 36
d) (2x – 3)(x + 5)
Lời giải hướng dẫn chi tiết:
a) 5x2 – 3x + 1
– Xét tam thức f(x) = 5x2 – 3x + 1
– Ta có: Δ = b2 – 4ac = 9 – 20 = –11 < 0 nên f(x) cùng dấu với hệ số a.
– Mà a = 5 > 0 ⇒ f(x) > 0 với ∀ x ∈ R.
b) -2x2 + 3x + 5
– Xét tam thức f(x) = –2x2 + 3x + 5
– Ta có: Δ = b2 – 4ac = 9 + 40 = 49 > 0.
– Tam thức có hai nghiệm phân biệt x1 = –1; x2 = 5/2, hệ số a = –2 < 0
– Ta có bảng xét dấu:

f(x) > 0 khi x ∈ (–1; 5/2)- Từ bảng xét dấu ta có:
f(x) = 0 khi x = –1 ; x = 5/2
f(x) < 0 khi x ∈ (–∞; –1) ∪ (5/2; +∞)
c) x2 + 12x + 36
– Xét tam thức f(x) = x2 + 12x + 36
– Ta có: Δ = b2 – 4ac = 144 – 144 = 0.
– Tam thức có nghiệm kép x = –6, hệ số a = 1 > 0.
– Ta có bảng xét dấu:

– Từ bảng xét dấu ta có:
f(x) > 0 với ∀x ≠ –6
f(x) = 0 khi x = –6
d) (2x – 3)(x + 5)
– Xét tam thức f(x) = 2x2 + 7x – 15
– Ta có: Δ = b2 – 4ac = 49 + 120 = 169 > 0.
– Tam thức có hai nghiệm phân biệt x1 = 3/2; x2 = –5, hệ số a = 2 > 0.
– Ta có bảng xét dấu:

– Từ bảng xét dấu ta có:
f(x) > 0 khi x ∈ (–∞; –5) ∪ (3/2; +∞)
f(x) = 0 khi x = –5 ; x = 3/2
f(x) < 0 khi x ∈ (–5; 3/2)
Bài 2 trang 105 SGK Đại Số 10: Lập bảng xét dấu của biểu thức
a) f(x) = (3x2 – 10x + 3)(4x – 5)
b) f(x) = (3x2 – 4x)(2x2 – x – 1)
c) f(x) = (4x2 – 1)(–8x2 + x – 3)(2x + 9)
d) f(x) = [(3x2 – x)(3 – x2)]/[4x2 + x – 3]
Lời giải hướng dẫn chi tiết:
a) f(x) = (3x2 – 10x + 3)(4x – 5)
– Tam thức 3x2 – 10x + 3 có hai nghiệm x = 1/3 và x = 3, hệ số a = 3 > 0 nên mang dấu + nếu x < 1/3 hoặc x > 3 và mang dấu – nếu 1/3 < x < 3.
– Nhị thức 4x – 5 có nghiệm x = 5/4.
– Ta có bảng xét dấu:
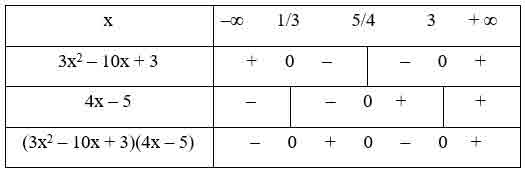
– Từ bảng xét dấu ta có:
f(x) > 0 khi x ∈ (1/3; 5/4) ∪ x ∈ (3; +∞)
f(x) = 0 khi x ∈ S = {1/3; 5/4; 3}
f(x) < 0 khi x ∈ (–∞; 1/3) ∪ (5/4; 3)
b) f(x) = (3x2 – 4x)(2x2 – x – 1)
– Tam thức 3x2 – 4x có hai nghiệm x = 0 và x = 4/3, hệ số a = 3 > 0.
⇒ 3x2 – 4x mang dấu + khi x < 0 hoặc x > 4/3 và mang dấu – khi 0 < x < 4/3.
+ Tam thức 2x2 – x – 1 có hai nghiệm x = –1/2 và x = 1, hệ số a = 2 > 0
⇒ 2x2 – x – 1 mang dấu + khi x < –1/2 hoặc x > 1 và mang dấu – khi –1/2 < x < 1.
– Ta có bảng xét dấu:

– Từ bảng xét dấu ta có:
f(x) > 0 ⇔ x ∈ (–∞; –1/2) ∪ (0; 1) ∪ (4/3; +∞)
f(x) = 0 ⇔ x ∈ S = {–1/2; 0; 1; 4/3}
f(x) < 0 ⇔ x ∈ (–1/2; 0) ∪ (1; 4/3)
c) f(x) = (4x2 – 1)(–8x2 + x – 3)(2x + 9)
– Tam thức 4x2 – 1 có hai nghiệm x = –1/2 và x = 1/2, hệ số a = 4 > 0
⇒ 4x2 – 1 mang dấu + nếu x < –1/2 hoặc x > 1/2 và mang dấu – nếu –1/2 < x < 1/2
– Tam thức –8x2 + x – 3 có Δ = –47 < 0, hệ số a = –8 < 0 nên luôn luôn âm.
– Nhị thức 2x + 9 có nghiệm x = –9/2.
– Ta có bảng xét dấu:

– Từ bảng xét dấu ta có:
f(x) > 0 khi x ∈ (–∞; –9/2) ∪ (–1/2; 1/2)
f(x) = 0 khi x ∈ S = {–9/2; –1/2; 1/2}
f(x) < 0 khi x ∈ (–9/2; –1/2) ∪ (1/2; +∞)
d) f(x) = [(3x2 – x)(3 – x2)]/[4x2 + x – 3]
– Tam thức 3x2 – x có hai nghiệm x = 0 và x = 1/3, hệ số a = 3 > 0.
⇒ 3x2 – x mang dấu + khi x < 0 hoặc x > 1/3 và mang dấu – khi 0 < x < 1/3.
– Tam thức 3 – x2 có hai nghiệm x = √3 và x = –√3, hệ số a = –1 < 0
⇒ 3 – x2 mang dấu – khi x < –√3 hoặc x > √3 và mang dấu + khi –√3 < x < √3.
– Tam thức 4x2 + x – 3 có hai nghiệm x = –1 và x = 3/4, hệ số a = 4 > 0.
⇒ 4x2 + x – 3 mang dấu + khi x < –1 hoặc x > 3/4 và mang dấu – khi –1 < x < 3/4.
– Ta có bảng xét dấu:

– Từ bảng xét dấu ta có:
f(x) > 0 ⇔ x ∈ (–√3; –1) ∪ (0; 1/3) ∪ (3/4; √3)
f(x) = 0 ⇔ x ∈ S = {±√3; 0; 1/3}
f(x) < 0 ⇔ x ∈ (–∞; –√3) ∪ (–1; 0) ∪ (1/3; 3/4) ∪ (√3; +∞)
f(x) không xác định khi x = -1 và x = 3/4.
Dạng 2: Giải các bất phương trình bậc 2 một ẩn:
Bài 3 trang 105 SGK Đại Số 10: Giải các bất phương trình sau
a) 4x2 – x + 1 < 0
b) -3x2 + x + 4 ≥ 0
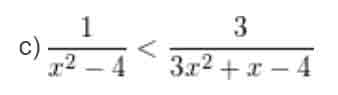
d) x2 – x – 6 ≤ 0
Lời giải hướng dẫn chi tiết:
a) 4x2 – x + 1 < 0
– Xét tam thức f(x) = 4x2 – x + 1
– Ta có: Δ = -15 < 0; a = 4 > 0 nên f(x) > 0 ∀x ∈ R
⇒ Bất phương trình đã cho vô nghiệm.
b) -3x2 + x + 4 ≥ 0
– Xét tam thức f(x) = -3x2 + x + 4
– Ta có : Δ = 1 + 48 = 49 > 0 có hai nghiệm x = -1 và x = 4/3, hệ số a = -3 < 0.
⇒ f(x) ≥ 0 khi -1 ≤ x ≤ 4/3. (Trong trái dấu a, ngoài cùng dấu với a)
⇒ Tập nghiệm của bất phương trình là: S = [-1; 4/3]
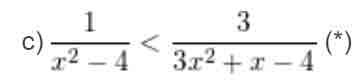
– Điều kiện xác định: x2 – 4 ≠ 0 và 3x2 + x – 4 ≠ 0
⇔ x ≠ ±2 và x ≠ 1; x ≠ 4/3.
– Chuyển vế và quy đồng mẫu chung ta được:
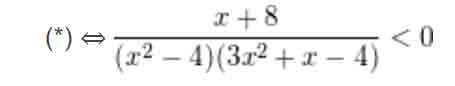
– Nhị thức x + 8 có nghiệm x = -8
– Tam thức x2 – 4 có hai nghiệm x = 2 và x = -2, hệ số a = 1 > 0
⇒ x2 – 4 mang dấu + khi x < -2 hoặc x > 2 và mang dấu – khi -2 < x < 2.
– Tam thức 3x2 + x – 4 có hai nghiệm x = 1 và x = -4/3, hệ số a = 3 > 0.
⇒ 3x2 + x – 4 mang dấu + khi x < -4/3 hoặc x > 1 mang dấu – khi -4/3 < x < 1.
– Ta có bảng xét dấu như sau:
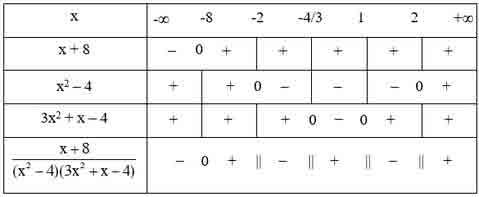
– Từ bảng xét dấu ta có:
(*) < 0 ⇔ x ∈ (–∞; –8) ∪ (-2; -4/3) ∪ (1; 2)
d) x2 – x – 6 ≤ 0
– Xét tam thức f(x) = x2 – x – 6 có hai nghiệm x = -2 và x = 3, hệ số a = 1 > 0
⇒ f(x) ≤ 0 khi -2 ≤ x ≤ 3.
⇒ Tập nghiệm của bất phương trình là: S = [-2; 3].
Dạng 3: Xác định tham số m thỏa điều kiện phương trình
Bài 4 trang 105 SGK Đại Số 10): Tìm các giá trị của tham số m để các phương trình sau vô nghiệm
a) (m – 2)x2 + 2(2m – 3)x + 5m – 6 = 0
b) (3 – m)x2 – 2(m + 3)x + m + 2 = 0
Lời giải hướng dẫn chi tiết:
a) (m – 2)x2 + 2(2m – 3)x + 5m – 6 = 0 (*)
• Nếu m – 2 = 0 ⇔ m = 2, khi đó phương trình (*) trở thành:
2x + 4 = 0 ⇔ x = -2 hay phương trình (*) có một nghiệm
⇒ m = 2 không phải là giá trị cần tìm.
• Nếu m – 2 ≠ 0 ⇔ m ≠ 2 ta có:
Δ’ = b’2 – ac = (2m – 3)2 – (m – 2)(5m – 6)
= 4m2 – 12m + 9 – 5m2 + 6m + 10m – 12
= -m2 + 4m – 3 = (-m + 3)(m – 1)
– Ta thấy (*) vô nghiệm ⇔ Δ’ < 0 ⇔ (-m + 3)(m – 1) < 0 ⇔ m ∈ (-∞; 1) ∪ (3; +∞)
– Vậy với m ∈ (-∞; 1) ∪ (3; +∞) thì phương trình vô nghiệm.
b) (3 – m)x2 – 2(m + 3)x + m + 2 = 0 (*)
• Nếu 3 – m = 0 ⇔ m = 3 khi đó (*) trở thành -6x + 5 = 0 ⇔ x = 5/6
⇒ m = 3 không phải là giá trị cần tìm.
• Nếu 3 – m ≠ 0 ⇔ m ≠ 3 ta có:
Δ’ = b’ – ac = (m + 3)2 – (3 – m)(m + 2)
= m2 + 6m + 9 – 3m – 6 + m2 + 2m
= 2m2 + 5m + 3 = (m + 1)(2m + 3)
– Ta thấy (*) vô nghiệm ⇔ Δ’ < 0 ⇔ (m + 1)(2m + 3) < 0 ⇔ m ∈ (-3/2; -1)
– Vậy với m ∈ (-3/2; -1) thì phương trình vô nghiệm.
Bài 53 trang 145 sgk Đại Số 10 nâng cao: Giải các bất phương trình
a) -5x2 + 4x + 12 < 0
b) 16x2 + 40x +25 < 0
c) 3x2 – 4x+4 ≥ 0
d) x2 – x – 6 ≤ 0
Lời giải hướng dẫn chi tiết:

b) Tam thức 16x2 +40x + 25 có:
∆’ = 202 – 16.25 = 0 và hệ số a = 16 > 0
Do đó; 16x2 +40x + 25 ≥ 0; ∀ x ∈ R
Suy ra, bất phương trình 16x2 +40x + 25 < 0 vô nghiệm
Vậy S = ∅
c) Tam thức 3x2 – 4x +4 có ∆’ = (-2)2 – 4.3 = -10 < 0
Hệ số a= 3 > 0
Do đó, 3x2 – 4x +4 ≥ 0; ∀ x ∈ R
Vậy tập nghiệm của bất phương trình đã cho là S = R.
d) Tam thức x2 – x – 6 có hai nghiệm là 3 và – 2
Hệ số a = 1 > 0 do đó, x2 – x – 6 khi và chỉ khi -2 ≤ x ≤ 3
Do đó, tập nghiệm của bất phương trình đã cho là S = [ – 2; 3].
a) Tập nghiệm T=(-∞;-6/5)∪(2;+∞)
b) Bất phương trình vô nghiệm vì Δ‘<0 và a = 16 > 0
c) Tập nghiệm là R vì 3x2-4x+4 có Δ‘<0 và hệ số a = 3 > 0
d) Tập nghiệm T=[-2;3]