Dưới đây là bài viết về Cách giải bài tập tập hợp các số nguyên dễ hiểu nhất được xây dựng một cách chi tiết, đầy đủ nhất cùng hướng dẫn giải bài tập toán lớp 6 kết nối tri thức với cuộc sống bài 13 để các bạn bồi dưỡng thế kiến thức. Điểu rõ hơn, mời các bạn tham khảo bài viết dưới đây.
Mục lục bài viết
1. Cách giải bài tập tập hợp các số nguyên dễ hiểu nhất:
*Dùng số nguyên để diễn tả các tình huống thực tiễn:
– Cách dùng để diễn tả nhiệt độ
+ Số nguyên âm được dùng để chỉ nhiệt độ dưới 0 độ C
+ Số nguyên dương được dùng để chỉ nhiệt độ trên 0 độ C
– Cách dùng để chỉ độ cao so với mực nước biển
+ Số nguyên âm được dùng để chỉ độ cao dưới mực nước biển.
+ Số nguyên dương được dùng để chỉ độ cao trên mực nước biển.
– Cách dùng để chỉ số tiền lãi (lỗ), số tiền nợ
+ Số nguyên âm được dùng để chỉ số tiền nợ, cũng như chỉ số tiền lỗ trong kinh doanh
+ Số nguyên dương được dùng để chỉ số tiền lãi trong kinh doanh.
– Cách dùng để chỉ thời gian trước và sau công nguyên
+ Số nguyên âm được dùng để chỉ thời gian trước công nguyên.
+ Số nguyên dương được dùng để chỉ thời gian sau công nguyên.
*Tập hợp số nguyên, phân biệt các số thuộc tập hợp số tự nhiên và số nguyên:
Phương pháp: Sử dụng định nghĩa các tập hợp số sau đây:
– Tập hợp số tự nhiên: N = { 0; 1; 2; 3; …}
– Tập hợp số tự nhiên khác 0: N* = { 1; 2; 3; …}
– Tập hợp số nguyên: Z = { -2; -1; 0; 1; 2; …}
+ Các số nguyên âm: -1; -2; -3; …
+ Các số nguyên dương: 1; 2; 3; …
Chú ý: Số 0 không là số nguyên âm cũng không là số nguyên dương.
*Biểu diễn các số nguyên trên trục số:
– Trên trục số nằm ngang:
+ Các điểm biểu diễn số nguyên âm nằm ở bên trái gốc 0
+ Các điểm biểu diễn số nguyên dương nằm ở bên phải gốc 0.
– Trên trục số thẳng đứng:
+ Các điểm biểu diễn số nguyên âm nằm ở bên dưới gốc 0
+ Các điểm biểu diễn số nguyên dương nằm ở bên trên gốc 0.
*Bài toán so sánh hai số nguyên:
– So sánh hai số nguyên trái dấu
Số nguyên âm luôn nhỏ hơn số nguyên dương.
– So sánh hai số nguyên cùng dấu
Để so sánh hai số nguyên âm, ta làm như sau:
Bước 1: Bỏ dấu “-” trước cả hai số âm.
Bước 2: Trong hai số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu (tương ứng) sẽ lớn hơn.
*Tìm số nguyên thuộc một khoảng cho trước:
Dựa vào qui tắc so sánh các số nguyên để chọn ra các số nguyên thích hợp.
Ví dụ:
Tìm số nguyên x thỏa mãn: -2 < x < 1
Ta thấy các số nguyên lớn hơn -2 nhỏ hơn 1 thỏa mãn đề bài nên x thuộc {-1; 0}.
2. Thứ tự trong tập số nguyên:
Câu hỏi 2 trang 60 Toán lớp 6 Tập 1:
Trên trục số, mỗi điểm sau nằm cách gốc O bao nhiêu đơn vị?
a) Điểm 2;
b) Điểm – 4
Đáp án hướng dẫn trả lời câu hỏi:
Ta có trục số sau:
![]()
Dựa vào trục số:
a) Điểm 2 cách gốc O một khoảng là 2 đơn vị
b) Điểm -4 cách gốc O một khoảng là 4 đơn vị.
Luyện tập 2 Toán lớp 6 trang 60 tập 1 KNTT:
Xuất phát từ gốc O, ta sẽ đi đến điểm nào nếu:
a) Di chuyển 5 đơn vị theo chiều dương?
b) Di chuyển 5 đơn vị theo chiều âm?
Đáp án hướng dẫn trả lời câu hỏi:
![]()
Dựa vào trục số: Xuất phát từ điểm gốc O
a) Di chuyển 5 đơn vị theo chiều dương ta sẽ đi đến điểm 5.
b) Di chuyển 5 đơn vị theo chiều âm ta sẽ đi đến điểm -5.
Hoạt động 3 Toán lớp 6 trang 60 tập 1 KNTT:
Trên trục số các số nguyên âm nằm trước hay sau gốc O? Từ đó em hãy sắp xếp ba số 0, 1 và – 1 theo thứ tự từ nhỏ đến lớn.
Đáp án hướng dẫn trả lời câu hỏi
Trên trục số các số nguyên âm nằm bên trái gốc O.
Vì -1 < 0 và 0 < 1 nên -1 < 0 < 1
Sắp xếp theo thứ tự từ nhỏ đến lớn: -1; 0; 1.
Hoạt động 4 Toán lớp 6 trang 60 tập 1 KNTT:
Quan sát trên trục số (h.3.6), ta thấy:
3 < 5 nhưng -3 > -5;
4 > 1 nhưng – 4 < -1.
Theo em, trong hai số – 12 và -15, số nào lớn hơn?
Đáp án hướng dẫn trả lời câu hỏi:
Do 12 < 15 nên -12 > -15.
Luyện tập 3 Toán lớp 6 trang 60 tập 1 KNTT:
1. Sắp xếp các số sau theo thứ tự tăng dần: 2; – 4; 0; 5; – 11; – 3; 9.
2. Trong tập {x ∈ Z| – 5 < x ≤ 2}, những số nào lớn hơn – 1?
Đáp án hướng dẫn trả lời câu hỏi:
1. +) Các số nguyên âm là: -4; -11; -3
Vì 11 > 4 > 3 nên -11 < -4 < -3 < 0 (1)
+) Các số nguyên dương là: 2; 5; 9
Ta có: 0 < 2 < 5 < 9 (2)
Từ (1) và (2) ta được: -11 < -4 < -3 < 0 < 2 < 5 < 9
Sắp xếp các số theo thứ tự tăng dần là: -11; -4; -3; 0; 2; 5; 9
2. Vì x là số nguyên lớn hơn – 5 và nhỏ hơn hoặc bằng 2 nên x là: -4; -3; -2; -1; 0; 1; 2
Các số nguyên lớn hơn -1 trong tập trên là: 0; 1; 2
Vậy x ∈ {0;1;2}.
Vận dụng 2 trang 60 SGK Toán 8 tập 1 KNTT:
Nhiệt độ trung bình vào tháng Giêng của ba thành phố lớn của nước Nga được ghi lại trong bảng bên (theo Wikipedia).
| Thành phố | Nhiệt độ (oC) |
| Moscow | -9 |
| Saint Peterburg | -8 |
| Vladivostok | -9 |
Hãy sắp xếp ba thành phố trên theo thứ tự giảm dần về nhiệt độ. Theo em thời tiết ở nơi nào lạnh hơn cả?
Đáp án hướng dẫn trả lời câu hỏi:
Do 12 > 9 > 8 nên -8 > -9 > -12 nên:
Sắp xếp ba thành phố theo thứ tự giảm dần về nhiệt độ: Saint Peterburg, Moscow, Vladivostok
Thời tiết ở Vladivostok lạnh hơn cả.
Tranh luận trang 61 Toán lớp 6 Tập 1:
Giả sử một con kiến bò trên sợi dây (giống như một trục số). Nếu nó đi được 4 đơn vị theo chiều dương, ta nói kiến bò được 4 đơn vị; nếu nó đi được 4 đơn vị nhưng theo chiều âm, ta nói kiến bò được – 4 đơn vị.
a) Em hiểu thế nào nào nếu nói: “Kiến A bò được 12 đơn vị” và “Kiến B bò được – 15 đơn vị”?
b) Từ nhận xét rằng 12 > – 15, An kết luận: kiến A bò được quãng đường dài hơn kiến B. Em có đồng ý với An không?
Đáp án hướng dẫn trả lời câu hỏi:
a) Nếu nói: “Kiến A bò được 12 đơn vị” được hiểu là kiến A bò được 12 đơn vị theo chiều dương.
“Kiến bò được – 15 đơn vị” được hiểu là kiến B bò được 15 đơn vị theo chiều âm.
b) Từ nhận xét rằng 12 > – 15, An kết luận: Kiến A bò được quãng đường dài hơn kiến B. Em không đồng ý với An vì:
Vì độ dài quãng đường không âm nên:
Kiến A bò được quãng đường là 12 đơn vị, kiến B bò được quãng đường là 15 đơn vị. Mà 12 < 15 nên kiến A bò được quãng đường ngắn hơn kiến B.
3. Giải Toán lớp 6 Kết nối tri thức với cuộc sống Bài 13:
Bài 3.1 trang 61 Toán lớp 6 tập 1 KNTT:
Hướng dẫn giải chi tiết bài tập:
Nhiệt độ mồi nhiệt kế chỉ lần lượt là: -8 ; 31 ; 0 ; -22
Bài 3.2 trang 61 Toán lớp 6 tập 1 KNTT:
Hãy thử sử dụng số nguyên âm để diễn tả lại ý nghĩa của các câu sau đây:
a) Độ sâu trung bình của vịnh Thái Lan khoảng 45m và độ sâu lớn nhất là 80m dưới mực nước biển;
b) Mùa đông ở Siberia (Nga) dài và khắc nghiệt với nhiệt độ trung bình tháng 1 là 25∘C dưới 0∘C
c) Năm 2012, núi lửa Harve (Bắc New Zealand) phun ra cột tro từ độ sâu 700m dưới mực nước biển .
Hướng dẫn giải chi tiết bài tập:
a) Độ sâu trung bình của vịnh Thái Lan khoảng – 45m và độ sâu lớn nhất là – 80m ;
b) Mùa đông ở Siberia (Nga) dài và khắc nghiệt với nhiệt độ trung bình tháng 1 là – 25∘C
c) Năm 2012, núi lửa Harve (Bắc New Zealand) phun ra cột tro từ độ sâu – 700m .
Bài 3.3 trang 61 Toán lớp 6 tập 1 KNTT:
Em hiểu ý nghĩa của mỗi câu sau như thế nào (diễn tả bằng một câu không sử dụng số âm) :
a) Khi máy bay ở độ cao 10 000m, nhiệt độ bên ngoài có thể xuống đến – 50∘C
b) Cá voi xanh có thể lặn được – 2 500m
Hướng dẫn giải chi tiết bài tập:
a) Khi máy bay ở độ cao 10 000m, nhiệt độ bên ngoài có thể xuống đến 50∘C dưới 0∘C
b) Cá voi xanh có thể lặn được độ sâu 2 500m dưới mực nước biển
Bài 3.4 trang 61 Toán lớp 6 tập 1 KNTT:
Hãy biểu diễn các số sau đây trên cùng một trục số: 3; -3; -5; 6; -4; 4
Hướng dẫn giải chi tiết bài tập:
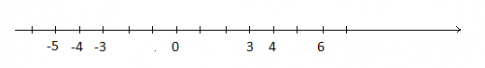
Bài 3.5 trang 61 Toán lớp 6 tập 1 KNTT:
Các điểm A, B, C, D và E trong hình dưới đây biểu diễn số nào?

Hướng dẫn giải chi tiết bài tập:
Các điểm A, B, C, D, E lần lượt biểu diễn các số: 9; -5; 5; 0; -1
Bài 3.6 trang 61 Toán lớp 6 tập 1 KNTT:
Hãy sắp xếp các số sau theo thứ tự tăng dần:
-3; +4; 7; -7; 0; -1; +15; -8; 25
Hướng dẫn giải chi tiết bài tập:
Ta có:
Các số nguyên âm là: -3; -7; -1; -8
Vì 8 > 7 > 3 > 1 nên -8 < -7 < -3 < -1 < 0 (*)
Các số nguyên dương là: 4; 7; 15; 25
Ta có: 0 < 4 < 7 < 15 < 25 (**)
Từ (1) và (2) ta được: -8 < -7 < -3 < -1 < 0 < 4 < 7 < 15 < 25
Bài 3.7 trang 61 Toán lớp 6 tập 1 KNTT:
Hãy so sánh hai số:
a) -39 và -54
b) – 3 719 và – 3 279
Hướng dẫn giải chi tiết bài tập:
a) Vì 39 < 54 nên -39 > -54;
b) Vì 3 179 < 3 279 nên – 3 179 > – 3 279.
Bài 3.8 trang 61 Toán lớp 6 tập 1 KNTT:
Liệt kê các phần tử của mỗi tập hợp sau:
a) A = {x ∈ Z| -2 ≤ x < 4};
b) B = {x ∈ Z| -2 < x ≤ 4}
Hướng dẫn giải chi tiết bài tập:
a) A = {-2; -1; 0; 1; 2; 3}
b) B = {-1; 0; 1; 2; 3; 4}
Tranh luận trang 61 Toán lớp 6 Tập 1 KNTT:
Giả sử một con kiến bò trên sợi dây (giống như một trục số). Nếu nó đi được 4 đơn vị theo chiều dương, ta nói kiến bò được 4 đơn vị; nếu nó đi được 4 đơn vị nhưng theo chiều âm, ta nói kiến bò được – 4 đơn vị.
a) Em hiểu thế nào nào nếu nói: “Kiến A bò được 12 đơn vị” và “Kiến B bò được – 15 đơn vị”?
b) Từ nhận xét rằng 12 > – 15, An kết luận: kiến A bò được quãng đường dài hơn kiến B. Em có đồng ý với An không?
Hướng dẫn giải chi tiết bài tập:
a) Nếu nói: “Kiến A bò được 12 đơn vị” được hiểu là kiến A bò được 12 đơn vị theo chiều dương.
“Kiến bò được – 15 đơn vị” được hiểu là kiến B bò được 15 đơn vị theo chiều âm.
b) Từ nhận xét rằng 12 > – 15, An kết luận: Kiến A bò được quãng đường dài hơn kiến B. Em không đồng ý với An vì:
Vì độ dài quãng đường không âm nên:
Kiến A bò được quãng đường là 12 đơn vị, kiến B bò được quãng đường là 15 đơn vị. Mà 12 < 15 nên kiến A bò được quãng đường ngắn hơn kiến B.