Phép tính tích phân giúp tìm ra nguyên hàm của hàm số. Những nguyên hàm này còn được gọi là tích phân của hàm số. Quá trình tìm nguyên hàm của một hàm số được gọi là tích phân. Quá trình ngược lại của việc tìm đạo hàm là tìm tích phân. Sau đây là các phương pháp tính tích phân từng phần cực hay và dễ hiểu.
Mục lục bài viết
1. Phương pháp tính tích phân từng phần cực hay và dễ hiểu:
1.1. Tích phân bằng cách đổi biến số:
Đôi khi, rất khó tìm được tích phân của một hàm, do đó chúng ta có thể tìm tích phân bằng cách đưa vào một biến độc lập mới. Phương pháp này được gọi là Tích phân bằng cách đổi biến số.
Dạng hàm tích phân đã cho (giả sử ∫f(x)) có thể được chuyển đổi thành dạng khác bằng cách thay đổi biến độc lập x thành t,
Thay x = g(t) vào hàm ∫f(x), ta nhận được;
dx/dt = g'(t)
hoặc dx = g'(t).dt
Do đó, I = ∫f(x).dx = f(g(t)).g'(t).dt
1.2. Tích phân từng phần:
Tích phân từng phần đòi hỏi một kỹ thuật đặc biệt để tích hợp một hàm, trong đó hàm tích phân là bội của hai hoặc nhiều hàm.
Chúng ta hãy coi một hàm tích phân là f(x).g(x).
Về mặt toán học, tích phân từng phần có thể được biểu diễn dưới dạng;
∫f(x).g(x).dx = f(x).∫g(x).dx–∫(f′(x).∫g(x).dx).dx
Trong đó:
Tích phân của tích hai hàm = (Hàm số thứ nhất × Tích phân của hàm số thứ hai) – Tích phân của [(vi phân của hàm số thứ nhất) × Tích phân của hàm số thứ hai]
Để quyết định hàm thứ nhất và hàm thứ hai, người ta có thể tuân theo quy tắc ILATE để tích phân.
1.3. Tích phân sử dụng nhận dạng lượng giác:
Trong phép tích phân của một hàm, nếu tích phân bao gồm bất kỳ loại hàm lượng giác nào thì chúng ta sử dụng các đẳng thức lượng giác để đơn giản hóa hàm có thể dễ dàng tích phân.
Một số nhận dạng lượng giác như sau:
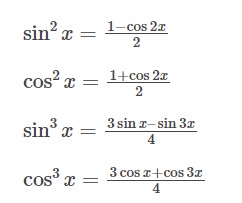
– Tích phân phối hợp
Tích phân của một số hàm cụ thể bao gồm một số công thức tích phân quan trọng có thể được áp dụng để thực hiện tích phân khác thành dạng tích phân chuẩn. Việc tích hợp các tích phân tiêu chuẩn này có thể dễ dàng được tìm thấy bằng cách sử dụng dạng phương pháp tích phân trực tiếp.
1.4. Tích phân của hàm phân thức hữu tỉ:
Tích phân của hàm phân thức hữu tỉ là một trong những chủ đề quan trọng trong giải tích. Để tính được tích phân của một hàm phân thức hữu tỉ, ta cần biết cách phân tích hàm số đó thành các hàm số đơn giản hơn, như hàm số mũ, lôgarit, lượng giác hay căn bậc hai. Một phương pháp phổ biến để làm điều này là sử dụng phương pháp phân số đơn vị (PSĐV), hay còn gọi là phương pháp phân số đơn thức. Phương pháp này dựa trên việc tìm các ước của tử số và mẫu số của hàm phân thức, sau đó viết lại hàm số đó dưới dạng tổng hoặc hiệu của các hàm số có mẫu số là các ước của mẫu số ban đầu. Sau khi đã có được dạng PSĐV, ta có thể tính tích phân của từng hàm số đơn vị bằng các công thức cơ bản hoặc bằng cách thực hiện các biến đổi thích hợp. Ví dụ, để tính tích phân của hàm số f(x) = (x^2 + 3x – 4) / (x^3 – x), ta có thể làm như sau:
Bước 1: Tìm các ước của tử số và mẫu số. Ta có:
Tử số: x^2 + 3x – 4 = (x + 4)(x – 1)
Mẫu số: x^3 – x = x(x^2 – 1) = x(x + 1)(x – 1)
Bước 2: Viết lại hàm số dưới dạng PSĐV. Ta có:
f(x) = (x^2 + 3x – 4) / (x^3 – x) = A / x + B / (x + 1) + C / (x – 1)
với A, B, C là các hằng số cần tìm.
Bước 3: Tìm các hằng số A, B, C bằng cách nhân hai vế của biểu thức trên với mẫu số chung x(x + 1)(x – 1), sau đó so sánh các hệ số của các luỹ thừa của x. Ta được:
A(x + 1)(x – 1) + Bx(x – 1) + Cx(x + 1) = x^2 + 3x – 4
Mở ngoặc và sắp xếp lại, ta được:
(A + B + C)x^2 + (A – B + C)x – (A + C) = x^2 + 3x – 4
So sánh các hệ số, ta được:
A + B + C = 1
A – B + C = 3
A + C = -4
Giải hệ này, ta được:
A = -5/3
B = -2/3
C = 4/3
Bước 4: Thay các giá trị của A, B, C vào biểu thức PSĐV và tính tích phân. Ta có:
f(x) = (-5/3) / x + (-2/3) / (x + 1) + (4/3) / (x – 1)
∫f(x)dx = (-5/3)∫(1/x)dx + (-2/3)∫(1/(x+1))dx + (4/3)∫(1/(x-1))dx
= (-5/3)ln|x| – (2/3)ln|x+1| + (4/3)ln|x-1| + C
với C là hằng số tích phân.
Đây là kết quả cuối cùng của tích phân của hàm phân thức hữu tỉ f(x).
2. Tích phân là gì?
Tích phân là một khái niệm và phạm trù toán học liên quan đến toàn bộ quá trình thay đổi của một thực thể nguyên thuỷ (thực thể đó thường được diễn tả bằng một hàm số phụ thuộc vào biến số được gọi là nguyên hàm) khi đã xác định được tốc độ thay đổi của nó. Tích phân cùng với khái niệm đối lập của nó, vi phân, đóng vai trò là 2 phép tính cơ bản và chủ chốt trong lĩnh vực giải tích. Một ví dụ cơ bản về vai trò của tích phân là ứng dụng của nó trong bài toán tính quãng đường của một chất điểm khi đã biết vận tốc của nó. Một ví dụ khác là bài toán tính thể tích một vật được tạo bởi một mặt phẳng xoay quanh trục cố định khi đã biết về diện tích hay mật độ trên mỗi mặt cắt của vật đó. Về mặt hình học, có thể hiểu đơn giản tích phân như là diện tích hoặc thể tích được tổng quát hóa.
Tích phân có nhiều loại khác nhau, nhưng hai loại quan trọng nhất là tích phân xác định và tích phân bất định. Tích phân xác định được ký hiệu là ∫b a f(x)dx, trong đó f(x) là hàm số cần tích phân, a và b là hai giới hạn của biến số x. Tích phân xác định có thể được hiểu là diện tích của vùng trong không gian phẳng xy được bao bởi đồ thị của hàm f, trục hoành, và các đường thẳng x = a và x = b. Tích phân xác định có thể được tính bằng công thức Newton-Leibniz: ∫b a f(x)dx = F(b) – F(a), trong đó F(x) là nguyên hàm của f(x), tức là F'(x) = f(x).
Tích phân bất định được ký hiệu là ∫f(x)dx, trong đó không có giới hạn cho biến số x. Tích phân bất định có thể được hiểu là tập hợp tất cả các nguyên hàm của f(x), tức là tất cả các hàm số F(x) sao cho F'(x) = f(x). Tích phân bất định có thể được tính bằng các công thức tích phân cơ bản hoặc các phương pháp tích phân như: tích phân từng phần, tích phân bằng cách phân tích, tích phân đổi biến số, vi phân.
3. Bài tập vận dụng:
Bài 1: Tính tích phân 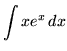
Lời giải:
Đặt ![]() và
và ![]()
Ta có: ![]() và
và ![]()
Vì vậy, ![]()
![]()
Bài 2: Tính tích phân 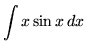
Lời giải:
Đặt: ![]() và
và ![]()
Ta có: ![]() và
và ![]()
Vì vậy: ![]()
Bài 3: Tính tích phân ![]()
Lời giải:
Đặt: ![]() và
và ![]()
Ta có: ![]() và
và 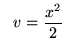
Vì vậy,
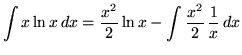
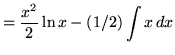
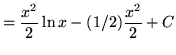
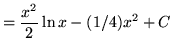
Bài 4: Tính tích phân![]()
Lời giải:
Đặt:![]() và
và ![]()
Ta có:![]() và
và ![]()
Vì vậy,
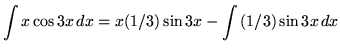
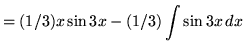
![]()
![]()
Bài 5: Tính tích phân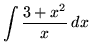
Lời giải:
Đầu tiên, chia hàm hữu tỉ này thành hai phần. Ta có:

(Bây giờ hãy sử dụng công thức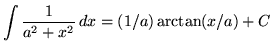 và lưu ý rằng 3C được thay thế bằng C vì C là hằng số tùy ý.)
và lưu ý rằng 3C được thay thế bằng C vì C là hằng số tùy ý.)
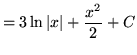
Bài 6: Tính tích phân 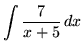
Lời giải:
Sử dụng u thay thế, ta có:![]()
Vì vậy:![]()
Thay vào tích phân ban đầu, thay mọi x, ta được: 
(Bây giờ hãy sử dụng công thức 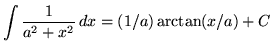 và lưu ý rằng 7C được thay thế bằng C vì C là hằng số tùy ý.)
và lưu ý rằng 7C được thay thế bằng C vì C là hằng số tùy ý.)

Bài 7: Tính tích phân 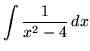
Lời giải:
Chuyển thành phân thức đơn giản, ta được

(Sau khi có được mẫu số chung, cộng các phân số và các tử số bằng nhau, ta được:
![]() ;
;
Nếu![]() ;
;
Nếu![]() .)
.)
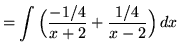
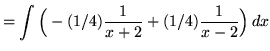
![]()
![]()
(mà ![]() .)
.)
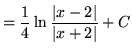
Bài 8: Tính tích phân 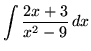
Lời giải:
Chuyển thành phân thức đơn giản, ta được

(Sau khi có được mẫu số chung, cộng các phân số và các tử số bằng nhau, ta được:![]() ;
;
Nếu![]() ;
;
Nếu![]() .)
.)
 .
.




