Hệ phương trình đối xứng loại 1 là một dạng toán thú vị trong chương trình toán học, nơi mà các phương trình có tính chất đối xứng qua hai biến số. Dưới đây là bài viết với chủ đề hướng dẫn giải hệ phương trình đối xứng loại 1 lớp 9. Xin mời các em học sinh cùng theo dõi.
Mục lục bài viết
1. Cách giải hệ phương trình đối xứng loại 1:
Bước 1: Đặt S = x + y, P = xy. Điều kiện: S2 ≥ 4P.
Bước 2: Biến đổi Hệ phương trình có hai ẩn S, P giải ra S và P (sử dụng phương pháp thế hoặc cộng đại số).
Bước 3: Tìm được S và P, khi đó x và y là nghiệm của phương trình bậc hai:
X2 – SX + P = 0
Giải phương trình bậc hai theo ẩn X.
Bước 4: Kết luận nghiệm của hệ phương trình.
Chú ý: Nếu (x0; y0) là nghiệm của hệ phương trình thì (y0; x0) cũng là nghiệm của hệ phương trình.
2. Hệ phương trình đối xứng loại 1:
2.1. Khái niệm hệ phương trình đối xứng loại 1:
Hệ phương trình đối xứng loại I theo ẩn x và y là Hệ phương trình mà khi ta đổi vai trò của các ẩn x và y thì hệ phương trình vẫn không thay đổi.
Hệ phương trình đối xứng loại 1 là hệ phương trình có dạng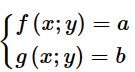 
(I), trong đó f (x; y), g (x; y) là các biểu thức đối xứng, tức là f (x; y) = f (y; x), g (x; y) = g (y; x).
2.2. Một số biểu diễn biểu thức đối xứng qua S và P:
Đặt S = x + y, P = x . y
x² + y² = (x + y)² – 2xy = S² – 2P
x³ + y³ = (x + y) . (x² + y² – xy) = S³ – 3SP
x²y + y²x = xy . (x + y) = SP
x⁴ + y⁴ = (x² + y²) – 2x²y² = (S² – 2P)² – 2P²
3. Các bài tập vận dụng liên quan:
Bài 1: Giải hệ phương trình: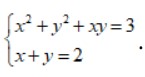 
Lời giải chi tiết:
Ta có:
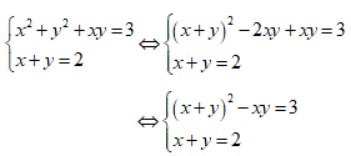
Đặt S = x + y, P = x . y. Điều kiện: S² >= 4P.
Ta có hệ:
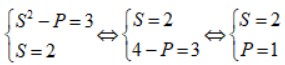(thỏa mãn)
x và y là nghiệm của phương trình bậc hai.
X² – 2X + 1 = 0
⇔ (X – 1)² = 0
⇔ X = 1
Vậy hệ phương trình có nghiệm là (1; 1).
Bài 2: Giải hệ phương trình: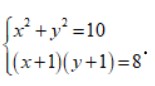 
Lời giải chi tiết:
Ta có:
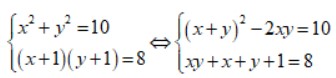
Đặt S = x + y, P = x . y. Điều kiện: S² >= 4P.
Ta có hệ phương trình:
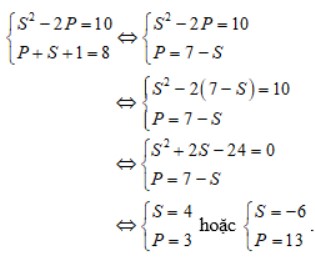
Mà S² >= 4P => S = 4, P = 3 thỏa mãn.
Khi đó x và y là nghiệm của phương trình bậc hai.
Vậy hệ phương trình có nghiệm là (1; 3) và (3; 1).
Bài 3: Giải hệ phương trình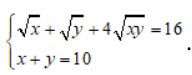 
Lời giải chi tiết:
Điều kiện xác định: x ≥ 0; y ≥ 0.
Đặt S = √x + √y; P = √xy
Điều kiện: S² >/ 4P và S >= 0; P >= 0
Ta có hệ phương trình:
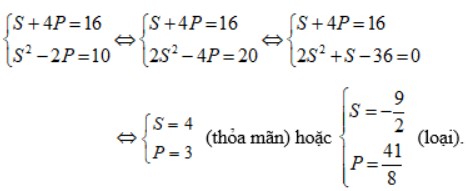
Khi đó √x và √y là nghiệm của phương trình bậc hai.
X² – 4X + 3 =0
⇔ (X – 1) . (X – 3) =0
⇔ X = 1 hoặc X = 3
Ta có: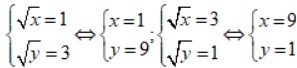 
Vậy hệ phương trình có nghiệm là (1; 9) và (9; 1).
4. Bài tập trắc nghiệm kèm đáp án:
Câu 1: Hệ phương trình sau có bao nhiêu nghiệm?
A. 1
B. 2
C. 3
D. 4
Đáp án: B. 2
Lời giải chi tiết:
Đặt S = x + y, P = x . y. Điều kiện: S² >= 4P.
Ta có hệ phương trình:
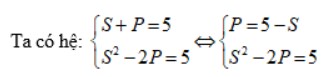
S² – 2 . (5 – S) = 5
⇔ S² + 2S – 15 = 0
=> (S – 3) . (S + 5) = 0
=> S = 4 hoặc S = -5
Với S = 3 => P = 2 (thỏa mãn)
Với S = -5 => P = 10 (loại)
Khi đó x và y là nghiệm của phương trình bậc hai.
X² – 3X + 2 = 0
⇔ (X – 1) . (X – 2) = 0
⇔ X = 1 hoặc X = 2
Vậy hệ phương trình có 2 nghiệm là (1; 2) và (2; 1).
Câu 2: Hệ phương trình sau có bao nhiêu nghiệm?
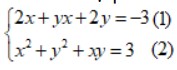
A. 1
B. 2
C. 3
D. 4
Đáp án:
Lời giải chi tiết:
Ta có:
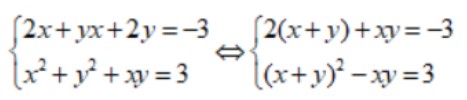
Đặt S = x + y, P = x . y. Điều kiện: S² >= 4P.
Ta có hệ phương trình:
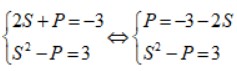
Thay P = – 3 – 2S vào phương trình (3) ta được:
S² – (-3 – 2S) = 3
⇔ S² + 3 + 2S = 3
⇔ S² + 2S = 0
⇔ S . (S + 2) = 0
⇔ S = 0 hoặc S = – 2
* Với S = 0 => P = -3 (thỏa mãn). Khi đó x và y là nghiệm của phương trình bậc hai.
X² – 3 = 0
⇔ (X – √3) . (X + √3) = 0
⇔ X = √3 hoặc X = – √3
Suy ra hệ có 2 nghiệm là (√3; -√3) và (-√3; √3).
* Với S = – 2 => P = 1 (thỏa mãn). Khi đó x và y là nghiệm của phương trình bậc hai.
X² + 2X + 1 = 0
⇔ (X + 1)² = 0
⇔ X = – 1
Suy ra hệ có 1 nghiệm là (-1; -1).
Vậy hệ phương trình có 3 nghiệm là (√3; -√3); (-√3; √3) và (-1; -1).
Câu 3: Hệ phương trình sau có bao nhiêu nghiệm?
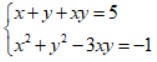
A. 1
B. 2
C. 3
D. 4
Đáp án: D. 4
Lời giải chi tiết:
Ta có:
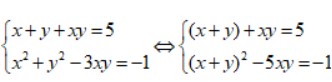
Đặt S = x + y, P = x . y. Điều kiện: S² >= 4P.
Ta có hệ phương trình:
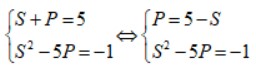
Thay P = 5 – S vào phương trình (3) ta được:
S² – 5. (5 – S) = – 1
⇔ S² + 5S – 25 = – 1
⇔ S² + 5S – 24 = 0
⇔ (S – 3) . (S + 8) = 0
⇔ S = – 8 hoặc S = 3
* Với S = – 8 => P = 13 (thỏa mãn). Khi đó x và y là nghiệm của phương trình bậc hai.
X² + 8X + 13 = 0
⇔ X = – 4 – √3 hoặc X = – 4 + √3.
* Với S = 3 => P = 2 (thỏa mãn). Khi đó x và y là nghiệm của phương trình bậc hai.
X² – 3X + 2 = 0
⇔ (X – 1) . (X – 2) = 0
⇔ X = 1 hoặc X = 2
Suy ra hệ có 2 nghiệm là (1; 2) và (2; 1).
Vậy hệ phương trình có 4 nghiệm là (1; 2); (2; 1), (- 4 – √3; – 4 + √3), (- 4 + √3; – 4 – √3).
Câu 4:
Hệ phương trình sau: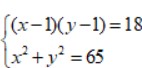 
. Cách giải hệ phương trình đối xứng loại 1 cực hay. Chọn nghiệm đúng của hệ phương trình.
A. (4;7) và (7;4)
B. (-1;-8) và (-8;-1)
C. (1;2) và (2;1)
D. A và B
Đáp án: D. A và B
Lời giải chi tiết:
Ta có: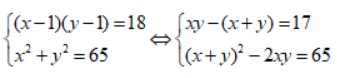 
Đặt S = x + y, P = x . y. Điều kiện: S² >= 4P.
Ta có hệ phương trình:
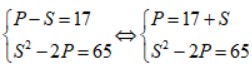
Thay P = 17 + S vào phương trình (3) ta được:
S² – 2 . (17 + S) = 65
⇔ S² – 2S – 99 = 0
⇔ (S + 9) . (S – 11) = 0
⇔ S = – 9 hoặc S = 11
* Với S = – 9 => P = 8 (thỏa mãn). Khi đó x và y là nghiệm của phương trình bậc hai.
X² + 9X + 8 = 0
⇔ (X + 1) . (X + 8) = 0
⇔ X = – 1 hoặc X = – 8
Suy ra hệ có 2 nghiệm là:(–1; –8); (–8; –1);
* Với S = 11 ⇒ P = 28 (thỏa mãn). Khi đó x và y là nghiệm của phương trình bậc hai.
X² – 11X + 28 = 0
⇔ (X – 4) . (X – 7) = 0
⇔ X = 4 hoặc X = 7
Suy ra hệ có 2 nghiệm là (4;7); (7;4)
Vậy hệ phương trình có 4 nghiệm là: (4;7); (7;4); (–1;–8); (–8;–1).
Câu 5: Hệ phương trình sau: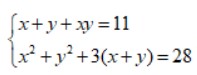 
. Đâu không phải là nghiệm đúng của hệ phương trình.
A. (1;6) và (6;1)
B. (2;3) và (3;2)
C. (–3;–7)
D. (–7;–3)
Đáp án:
Lời giải chi tiết:
Ta có:
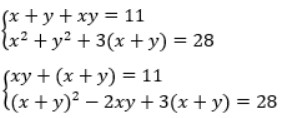
Đặt S = x + y, P = x . y. Điều kiện: S² >= 4P.
Ta có hệ phương trình:
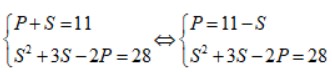
Thay P = 11 – S vào phương trình (3) ta được:
S² + 3S – 2 . (11 – S) = 28
⇔ S² + 5S – 50 = 0
⇔ (S + 10) . (S – 5) = 0
⇔ S = – 10 hoặc S = 5
* Với S = – 10 => P = 21 (thỏa mãn). Khi đó x và y là nghiệm của phương trình bậc hai.
X² + 10X + 21 = 0
⇔ (X + 3) . (X + 7) = 0
⇔ X = – 3 hoặc X = – 7
Suy ra hệ có 2 nghiệm là:(–3; –7); (–7; –3);
* Với S = 5 ⇒ P = 6 (thỏa mãn), Khi đó x và y là nghiệm của phương trình bậc hai.
X² – 5X + 6 = 0
⇔ (X – 2) . (X – 3) = 0
⇔ X = 2 hoặc X = 3
Suy ra hệ có 2 nghiệm là (2; 3); (3;2);
Vậy hệ phương trình có 4 nghiệm là: (2; 3); (3;2); (–3; –7); (–7; –3).
THAM KHẢO THÊM:
