Việc xác định vị trí tương đối của hai đường thẳng trong không gian là một phần quan trọng của hình học không gian và có thể được thực hiện dễ dàng bằng cách sử dụng tính chất có hướng và xem xét theo sơ đồ. Mời các bạn cùng tham khảo bài viết dưới đây.
Mục lục bài viết
1. Vị trí tương đối của hai đường thẳng trong không gian:
Trong không gian ba chiều, việc xác định vị trí tương đối của hai đường thẳng là một phần quan trọng của hình học không gian. Có hai trường hợp chính mà hai đường thẳng có thể nằm trong:
I. Hai đường thẳng đồng phẳng:
Hai đường thẳng được coi là đồng phẳng khi chúng nằm trên cùng một mặt phẳng trong không gian. Có ba trường hợp cơ bản về vị trí tương đối của hai đường thẳng đồng phẳng:
– Cắt nhau: Trong trường hợp này, hai đường thẳng có duy nhất một điểm chung. Nếu bạn vẽ hai đường thẳng và chúng gặp nhau ở một điểm, thì chúng đang cắt nhau.
– Song song: Hai đường thẳng được gọi là song song khi chúng nằm trên cùng một mặt phẳng nhưng không có điểm chung nào. Điều này có nghĩa rằng nếu bạn vẽ hai đường thẳng và chúng chạy trên cùng một mặt phẳng mà không gặp nhau, thì chúng là hai đường thẳng song song.
– Trùng nhau: Hai đường thẳng trùng nhau khi chúng hoàn toàn trùng với nhau. Nếu bạn vẽ hai đường thẳng và chúng trùng với nhau ở nhiều điểm, thì chúng là hai đường thẳng trùng nhau.
II. Hai đường thẳng không đồng phẳng:
Trường hợp này xảy ra khi hai đường thẳng không nằm trong cùng một mặt phẳng. Chúng không có điểm chung nào và thường được gọi là hai đường thẳng chéo nhau.
Để xác định vị trí tương đối của hai đường thẳng trong không gian, ta có thể sử dụng hai tiêu chí chính: số điểm chung và sự đồng phẳng. Tuy nhiên, trong không gian ba chiều, việc xét vị trí tương đối theo hai tiêu chí này có thể trở nên phức tạp và tính toán dài dòng.
Để đơn giản hóa việc xác định vị trí tương đối của hai đường thẳng trong không gian, chúng ta có thể sử dụng tính chất có hướng và xét theo sơ đồ. Tức là, ta có thể xem xét hình dáng và hướng của hai đường thẳng để xác định liệu chúng có thể cắt nhau, song song hay chéo nhau mà không cần phải thực hiện tính toán chi tiết. Việc này giúp tiết kiệm thời gian và giảm thiểu khả năng mắc lỗi trong quá trình xác định vị trí tương đối của hai đường thẳng trong không gian.
Tóm lại, việc xác định vị trí tương đối của hai đường thẳng trong không gian là một phần quan trọng của hình học không gian và có thể được thực hiện dễ dàng bằng cách sử dụng tính chất có hướng và xem xét theo sơ đồ. Điều này giúp giảm bớt sự phức tạp và tối ưu hóa quá trình xác định vị trí của hai đường thẳng.
2. Vị trí tương đối của hai đường thẳng trong không gian:
Trong hình học không gian, việc xác định vị trí tương đối của hai đường thẳng rất quan trọng và có nhiều ứng dụng thực tế. Có một số phương pháp để xác định vị trí tương đối của hai đường thẳng, và dưới đây chúng ta sẽ tìm hiểu về các phương pháp này cũng như các trường hợp cụ thể.
Vị trí tương đối giữa đường thẳng d (đi qua M0 và có vectơ chỉ phương u→) và đường thẳng d’ (đi qua M’0 và có vectơ chỉ phương u’→)
– d và d’ cùng nằm trong một mặt phẳng ⇔ 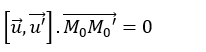
– d ≡ d’⇔ 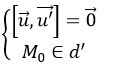
– d // d’ ⇔ 
– d và d’ cắt nhau: ⇔ 
– d và d’ chéo nhau ⇔ 
– 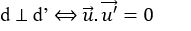
Tóm tắt:
Trong không gian ba chiều, việc xác định vị trí tương đối của hai đường thẳng có thể được thực hiện bằng nhiều phương pháp khác nhau, như việc kiểm tra việc cùng nằm trong một mặt phẳng, đồng quy, song song, cắt nhau hoặc chéo nhau. Tùy thuộc vào tính chất của hai đường thẳng và thông tin có sẵn, chúng ta có thể sử dụng các phương pháp khác nhau để xác định vị trí tương đối của chúng.
3. Bài tập về vị trí tương đối của hai đường thẳng trong không gian:
Bài tập vận dụng
Câu 1:
Trong hệ tọa độ không gian Oxyz, cho đường thẳng 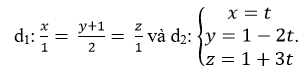 . Chọn khẳng định đúng?
. Chọn khẳng định đúng?
A. d1; d2 chéo nhau.
B. d1; d2cắt nhau.
C. d1; d2 vuông góc với nhau.
D.d1; d2 chéo nhau và vuông góc với nhau .
Lời giải:
+ Đường thẳng d1 đi qua A( 0; -1; 0); có vecto chỉ phương 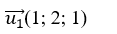
+ Đường thẳng d2 đi qua B(0; 1; 1); có vecto chỉ phương 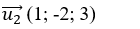
Ta có 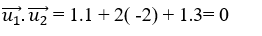
=> Hai vecto 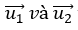 vuông góc với nhau. suy ra đường thẳng d1 vuông góc với d2.
vuông góc với nhau. suy ra đường thẳng d1 vuông góc với d2.
+ Mặt khác 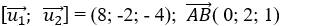
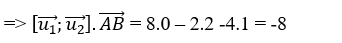
Suy ra d1 và d2 chéo nhau.
Chọn D.
Câu 2:
Trong không gian Oxyz, cho hai đường thẳng  . Trong các mệnh đề sau, mệnh đề nào đúng?
. Trong các mệnh đề sau, mệnh đề nào đúng?
A. song song.
B. trùng nhau.
C. cắt nhau.
D. chéo nhau.
Lời giải:
+ Đường thẳng d vecto chỉ phương 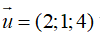 và đi qua M( 1; 7; 3)
và đi qua M( 1; 7; 3)
+ Đường thẳng d’ có vecto chỉ phương 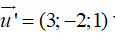 và đi qua M’( 6; -1; -2).
và đi qua M’( 6; -1; -2).
Từ đó ta có 
Lại có 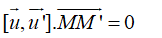
Suy ra d cắt d’.
Chọn C.
Câu 3:
Trong không gian Oxyz, cho hai đường thẳng 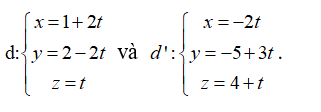 . Trong các mệnh đề sau, mệnh đề nào đúng?
. Trong các mệnh đề sau, mệnh đề nào đúng?
A. song song.
B. trùng nhau.
C. chéo nhau.
D. cắt nhau.
Lời giải:
Đường thẳng d có VTCP  và đi qua M(1;2; 0)
và đi qua M(1;2; 0)
Đường thẳng d’ có VTCP 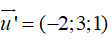 và đi qua M’(0;-5; 4)
và đi qua M’(0;-5; 4)
Từ đó ta có:

Lại có 
Suy ra d chéo nhau với d’.
Chọn C.
Câu 4:
Trong không gian Oxyz, cho hai đường thẳng 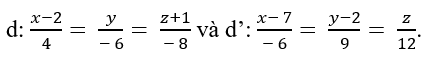 . Trong các mệnh đề sau, mệnh đề nào đúng khi nói về vị trí tương đối của hai đường thẳng trên?
. Trong các mệnh đề sau, mệnh đề nào đúng khi nói về vị trí tương đối của hai đường thẳng trên?
A. song song.
B. trùng nhau.
C. chéo nhau.
D. cắt nhau.
Lời giải:
Đường thẳng d có vecto chỉ phương 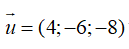 và đi qua M( 2; 0; -1)
và đi qua M( 2; 0; -1)
Đường thẳng d’ có vecto chỉ phương  và đi qua M’( 7; 2;0).
và đi qua M’( 7; 2;0).
Từ đó ta có 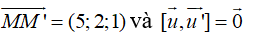
Lại có 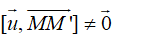
Suy ra d song song với d’.
Chọn A.
Câu 5:
Hai đường thẳng 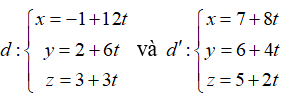 có vị trí tương đối là:
có vị trí tương đối là:
A. trùng nhau.
B. song song.
C. chéo nhau.
D. cắt nhau.
Lời giải:
Đường thẳng d có VTCP  và đi qua M(-1; 2; 3)
và đi qua M(-1; 2; 3)
Đường thẳng d’ có VTCP 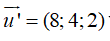 và đi qua M’ (7; 6; 5).
và đi qua M’ (7; 6; 5).
Từ đó ta có 
Suy ra 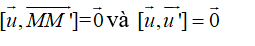
Suy ra d trùng với d’.
Chọn A.
Câu 6:
Trong không gian với hệ trục tọa độ Oxyz; cho đường thẳng  . Khi đó, giá trị của m bằng bao nhiêu thì d1 cắt d2?
. Khi đó, giá trị của m bằng bao nhiêu thì d1 cắt d2?
A. m= 0
B. m= 1
C. m= -2
D.Đáp án khác
Lời giải:
+ Đường thẳng d1: đi qua A(0; -2; 0) và nhận vecto 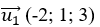 làm vecto chỉ phương
làm vecto chỉ phương
+ Đường thẳng d2: đi qua B( m; -2; 0) và nhận vecto 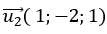 làm vecto chỉ phương
làm vecto chỉ phương

+ để hai đường thẳng d1 và d2 cắt nhau thì: 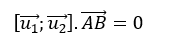 ⇔ 7.m + 5.0+ 3.0= 0 ⇔ 7m= 0 ⇔ m= 0
⇔ 7.m + 5.0+ 3.0= 0 ⇔ 7m= 0 ⇔ m= 0
Chọn A.
Câu 7:
Trong không gian với hệ tọa độ Oxyz; cho hai đường thẳng 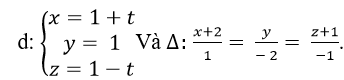 . Khẳng định nào sau đây là khẳng định đúng ?
. Khẳng định nào sau đây là khẳng định đúng ?
A. Δ cắt d và Δ vuông góc với d.
B. Δ và d chéo nhau, Δ vuông góc với d.
C. Δ cắt d và Δ không vuông góc với d .
D. Δ và d chéo nhưng không vuông góc.
Lời giải:
+ Đường thẳng d đi qua A( 1;1; 1) và có vecto chỉ phương  .
.
+ Đường thẳng Δ đi qua điểm B( – 2;0; -1) có véctơ chỉ phương là  .
.
+ Ta có 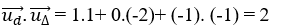 suy ra đường thẳng Δ không vuông góc với d.
suy ra đường thẳng Δ không vuông góc với d.
+ Mặt khác 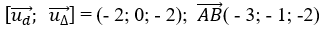

Suy ra Δ và d chéo nhau.
Chọn D.
Câu 8:
Cho hai đường thẳng 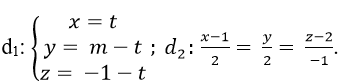 . Tìm m để hai đường thẳng đã cho chéo nhau?
. Tìm m để hai đường thẳng đã cho chéo nhau?
A. m ≠ -15
B. m ≠ -10
C. m ≠ 10
D. m ≠ 12
Lời giải:
+ Đường thẳng d1 đi qua A( 0; m;-1) và có vecto chỉ phương 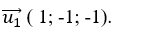 .
.
+ Đường thẳng d2 đi qua B( 1; 0; 2) và có vecto chỉ phương 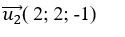
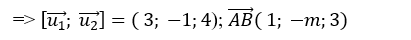
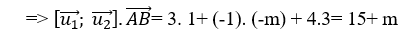
+ Để hai đường thẳng đã cho chéo nhau khi và chỉ khi: 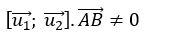 ⇔ 15+ m ≠ 0 hay m ≠ -15
⇔ 15+ m ≠ 0 hay m ≠ -15
Chọn A.
Câu 9:
Cho hai đường thẳng  . Tìm m để hai đường thẳng đã cho chéo nhau?
. Tìm m để hai đường thẳng đã cho chéo nhau?
A. m ≠ -1
B. m ≠ -10
C. m ≠ 10
D. m ≠ 12
Hướng dẫn giải
+ Đường thẳng d1 đi qua A( 2; 0;-1) và có vecto chỉ phương 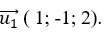 .
.
+ Đường thẳng d2 đi qua B( 0; m; – 1) và có vecto chỉ phương 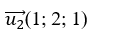

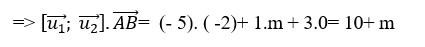
+ Để hai đường thẳng đã cho chéo nhau khi và chỉ khi:  ⇔ 10+ m ≠ 0 hay m ≠ -10
⇔ 10+ m ≠ 0 hay m ≠ -10
=> Chọn B.




