Trong chương trình toán học các bạn sẽ phải tìm hiểu về phép đối xứng tâm, đối xứng trục. Bài viết này chúng tôi sẽ cung cấp cho bạn kiến thức về phép đối xứng trục, các hình có trục đối xứng và các bài tập vận dụng.
Mục lục bài viết
1. Trục đối xứng là gì?
Trục đối xứng là một khái niệm quan trọng trong toán học và hình học, đó là đường thẳng hoặc một mặt phẳng chia một hình học thành hai phần đối xứng hoàn toàn với nhau. Trục đối xứng thường được sử dụng để diễn đạt về tính chất đối xứng của các hình học trong không gian. Ở mức độ cơ bản, trục đối xứng thường được xác định trong không gian hai chiều (phẳng). Nếu một hình học, ví dụ như một đa giác, được chia thành hai phần đối xứng qua một đường thẳng, thì mỗi điểm trên một phần sẽ có điểm đối xứng tương ứng trên phần còn lại qua đường trục đối xứng đó. Điều này có nghĩa là khoảng cách từ mỗi điểm đến trục đối xứng là bằng nhau. Tuy nhiên, trục đối xứng không chỉ tồn tại trong không gian hai chiều mà còn áp dụng trong không gian ba chiều và các khía cạnh khác của toán học. Trong không gian ba chiều, một mặt phẳng có thể là trục đối xứng chia một vật thể thành hai phần đối xứng. Sự đối xứng thông qua trục đối xứng không chỉ giúp chúng ta hiểu về hình dạng của các hình học mà còn có ứng dụng rất rộng rãi trong nhiều lĩnh vực, từ vật lý, hình thức thiết kế đến khoa học máy tính và nhiều lĩnh vực khác. Trục đối xứng là một công cụ mạnh mẽ giúp chúng ta phân tích và hiểu rõ sự đối xứng trong không gian và các biến đổi của các hình học.
2. Thế nào là một hình có trục đối xứng?
Một hình có trục đối xứng là hình học mà có thể chia thành hai phần đối xứng hoàn toàn với nhau thông qua một đường thẳng hoặc một mặt phẳng gọi là trục đối xứng. Điều này có nghĩa là mỗi điểm trên một phần của hình đối xứng với một điểm tương ứng trên phần còn lại qua trục đối xứng. Đối với các hình học trong không gian hai chiều, như hình tròn, hình vuông, tam giác, một đường thẳng có thể được sử dụng làm trục đối xứng. Ví dụ, khi chia một hình tròn bằng một đường thẳng đi qua tâm của nó, mỗi điểm trên nửa hình tròn này sẽ có điểm đối xứng tương ứng trên nửa còn lại qua trục đối xứng. Điều này cũng áp dụng cho hình vuông khi chia bằng một đường chéo, hay tam giác khi chia qua một đường từ trọng tâm đến một đỉnh. Trong không gian ba chiều, một mặt phẳng có thể được sử dụng làm trục đối xứng để chia một đối tượng thành hai phần đối xứng. Ví dụ, khi chia một hình cầu bằng một mặt phẳng đi qua tâm của nó, mỗi điểm trên một nửa hình cầu sẽ có điểm đối xứng tương ứng trên nửa còn lại qua mặt phẳng đối xứng.
Một số đặc điểm của các hình có trục đối xứng bao gồm:
– Đối xứng tương đối: Mỗi điểm trên một phần của hình có trục đối xứng đều có điểm tương ứng trên phần còn lại qua trục đối xứng. Khoảng cách từ mỗi điểm đến trục đối xứng là bằng nhau.
– Tính chất giữa các phần: Hai phần của hình qua trục đối xứng là hoàn toàn đối xứng với nhau về hình dạng và kích thước.
– Sử dụng trong phân tích và thiết kế: Tính chất đối xứng này có ứng dụng rộng rãi trong nhiều lĩnh vực, từ hình thức thiết kế đến vật lý, toán học ứng dụng và nhiều lĩnh vực khác.
Một hình có trục đối xứng thường mang tính đẹp mắt và được ứng dụng rộng rãi trong nghệ thuật, kiến trúc và các lĩnh vực sáng tạo khác, vì đặc tính đối xứng này tạo nên sự cân đối và hài hòa.
3. Bài tập về một hình có trục đối xứng:
Câu 1. Trong các công trình dưới đây, có bao nhiêu công trình có trục đối xứng?

A. 1
B. 2
C. 3
D. 0
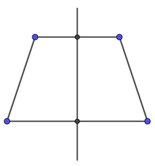
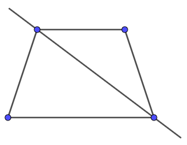
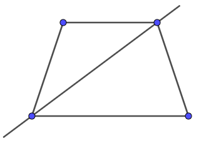
Câu 2. Hình nào dưới đây chỉ ra đúng trục đối xứng của hình thang cân?
A.
B.
C.
D.
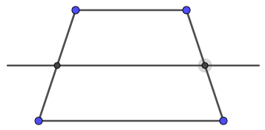
Lời giải Hình thang cân là hình có một trục đối xứng, trục đối xứng này nối hai trung điểm của hai cạnh đối song song như hình A 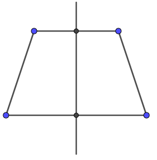
Câu 3. Hình nào dưới đây có vô số trục đối xứng
A. Hình lục giác đều
B. Hình vuông
C. Hình chữ nhật
D. Hình tròn
Câu 5. Hình nào dưới đây có trục đối xứng?

A. Hình a), Hình b), Hình c)
B. Hình a), Hình c), Hình d)
C. Hình b), Hình c), Hình d)
D. Hình a) và Hình c)
Câu 6. Hình vuông có bao nhiêu trục đối xứng:
A. 2
B. 3
C. 4
D. 0
Lời giải: Hình vuông có 4 trục đối xứng, trong đó:
+) 2 trục đối xứng là hai đường chéo của hình vuông. 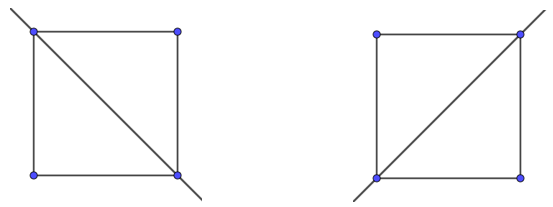
+) 2 trục đối xứng nối trung điểm của hai cạnh đối diện: 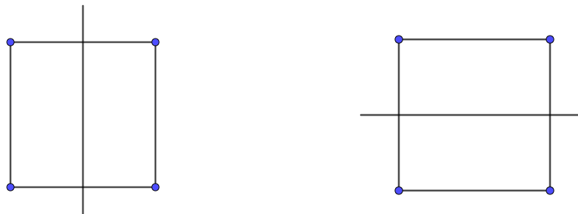
Đáp án: C
Câu 7. Trong các loại biển báo sau, biển báo nào có trục đối xứng?

A. Hình a) và Hình c)
B. Hình a) và Hình d)
C. Hình c) và Hình b)
D. Hình c) và Hình d)
Lời giải Hình a) và Hình c) là hai hình có trục đối xứng.
Câu 8. Hình nào có số trục đối xứng nhỏ nhất
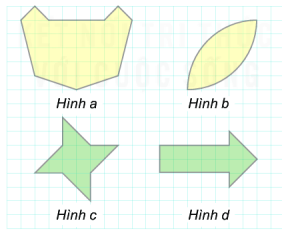
A. Hình a
B. Hình b
C. Hình c
D. Hình d
Lời giải:
Hình a) có 1 trục đối xứng: 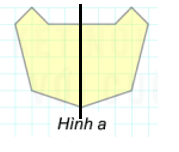
Hình b) có 1 trục đối xứng: 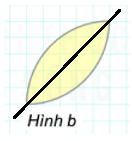
Hình c) không có trục đối xứng.
Hình d) có 1 trục đối xứng 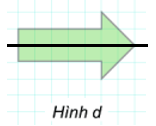
Đáp án: C
Câu 9. Phát biểu nào dưới đây là đúng?
A. Mỗi đường chéo là một trục đối xứng của hình chữ nhật.
B. Mỗi đường thẳng đi qua tâm một đường tròn là trục đối xứng của hình tròn.
C. Mỗi đường thẳng đi qua trung điểm của hai cạnh đối diện là trục đối xứng của hình thoi.
D. Mỗi đường chéo là một trục đối xứng của hình bình hành.
Lời giải Trục đối xứng của hình chữ nhật là hai đường thẳng đi qua trung điểm của hai cạnh đối nhau. Do đó A sai. Mỗi đường thẳng đi qua tâm một đường tròn là trục đối xứng của hình tròn. Do đó B đúng. Mỗi đường chéo là một trục đối xứng của hình thoi. Do đó C sai. Hình bình hành không có trục đối xứng. Do đó D sai.
Đáp án: B
Câu 10. Trong các chữ cái dưới đây, chữ cái có trục đối xứng?

A. A, H, E
B. A, H
C. A, B, H, E
D. B, E
Lời giải Trong các chữ cái trên có 4 chữ cái có trục đối xứng là: A, B, H, E.
Đáp án: C
Câu 11. Cho các phát biểu sau:
a) Hình vuông ABCD chỉ có hai trục đối xứng là hai đường chéo AC, BD.
b) Đường thẳng đi qua trung điểm của đoạn thẳng MN và vuông góc với MN là trục đối xứng của đoạn thẳng MN.
c) Nếu đường thẳng d là trục đối xứng của đường tròn thì d đi qua tâm của đường tròn ấy.
Số phát biểu đúng là:
A. 0
B. 1
C. 2
D. 3
Lời giải Phát biểu a) sai vì hình vuông có 4 trục đối xứng là AC, BD và hai trục đối xứng đi qua trung điểm của hai cạnh đối diện. Phát biểu b) là phát biểu đúng. Phát biểu c) là phát biểu đúng. Vậy có 2 phát biểu đúng.
Đáp án: C
Câu 12. Trong Hình 35, các hình từ a) đến e), hình nào có trục đối xứng?
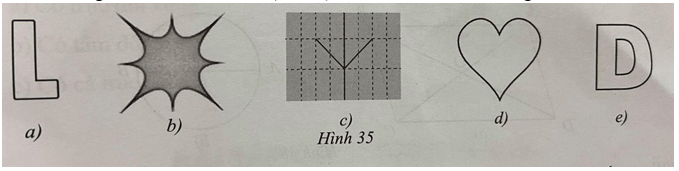
A. Hình 35a), 35b), 35c), 35e)
B. Hình 35b), 35c), 35d)
C. Hình 35b), 35c), 35d, 35e)
D. Hình 35a), 35c), 35d), 35e)
Lời giải Hình 35a) không có trục đối xứng nào. Hình 35b) có 4 trục đối xứng là các đường thẳng m, n, p, q. Hình 35c) có 1 trục đối xứng là đường thẳng x. Hình 35d) có 1 trục đối xứng là đường thẳng y. Hình 35e) có 1 trục đối xứng là đường thẳng z. 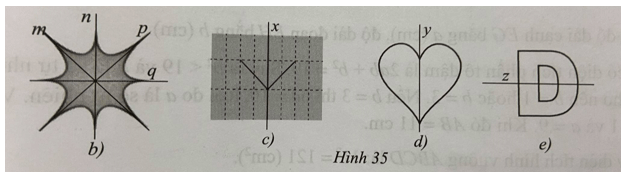
Đáp án: C
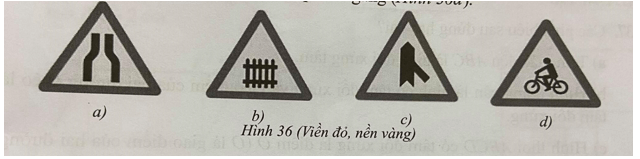
Câu 13. Trong các biển báo giao thông Hình 36, biển báo nào không có trục đối xứng?
a) Biển báo đường bị hẹp cả hai bên (Hình 36a);
b) Biển báo giao nhau với đường sắt có rào chắn (Hình 36b);
c) Biển báo giao nhau với đường không ưu tiên (Hình 36c);
d) Biển báo đường người đi xe đạp cắt ngang (Hình 36d).
A. Hình 36a), Hình 36b)
B. Hình 36a), Hình 36c)
C. Hình 36b), Hình 36c)
D. Hình 36c), Hình 36d)
Lời giải Hình 36a) và Hình 36b) là hình có trục đối xứng Hình 36c) và Hình 36d) là hình không có trục đối xứng.
Câu 14. Trong các công trình được minh họa ở Hình 37, các hình từ a) đến c), công trình nào có trục đối xứng?

A. Hình 37a)
B. Hình 37c) và Hình 37b)
C. Hình 37a) và Hình 37c)
D. Hình 37c)
Lời giải Công trình ở Hình 37a) và công trình ở Hình 37c) là có trục đối xứng.
Đáp án: C
Câu 15. Chữ cái nào dưới đây có hai trục đối xứng:

A. Chữ A
B. Chữ B
C. Chữ H
D. Chữ M
Lời giải:
Các chữ A, B, M đều có 1 trục đối xứng:

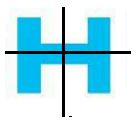
Chữ H là chữ có hai trục đối xứng:
Đáp án: C




