Tổng hợp kiến thức và các dạng bài tập Toán 3 cả năm tổng hợp các công thức Toán lớp 3 giúp cho các em học sinh hệ thống lại kiến thức cả năm học. Mời các bậc phụ huynh cùng các em học sinh tham khảo.
Mục lục bài viết
1. Các số đến 10000, 100000:
1.1. Đọc và viết:
Để đọc và viết các số có 4 chữ số, 5 chữ số, ta cần nhớ các quy tắc sau:
– Mỗi số có 4 chữ số gồm 4 hàng: hàng nghìn, hàng trăm, hàng chục và hàng đơn vị. Ví dụ: số 1234 có 1 nghìn, 2 trăm, 3 chục và 4 đơn vị.
– Mỗi số có 5 chữ số gồm 5 hàng: hàng chục nghìn, hàng nghìn, hàng trăm, hàng chục và hàng đơn vị. Ví dụ: số 12345 có 1 chục nghìn, 2 nghìn, 3 trăm, 4 chục và 5 đơn vị.
– Khi đọc một số có 4 chữ số, 5 chữ số, đọc theo thứ tự từ trái sang phải, bỏ qua các số 0. Ví dụ: số 1204 đọc là một nghìn hai trăm lẻ bốn; số 30050 đọc là ba mươi nghìn lẻ năm mươi.
– Khi viết một số có 4 chữ số, 5 chữ số theo cách đọc, viết theo thứ tự từ phải sang trái, thêm các số 0 vào các vị trí cần thiết. Ví dụ: ba nghìn bốn trăm viết là 3400; hai mươi nghìn ba trăm lẻ một viết là 20301.
* Bài tập
– Bài1: Đọc các số sau:
1234
5678
9101
2345
6789
Đáp án:
Một nghìn hai trăm ba mươi bốn
Năm nghìn sáu trăm bảy mươi tám
Chín nghìn một trăm linh một
Hai nghìn ba trăm bốn mươi lăm
Sáu nghìn bảy trăm tám mươi chín
– Bài 2: Viết các số sau:
Bốn nghìn ba trăm hai mươi mốt
Năm nghìn sáu trăm bảy mươi sáu
Chín nghìn không trăm linh chín
Một nghìn hai trăm ba mươi bảy
Sáu nghìn bảy trăm tám mươi hai
Đáp án:
4321
5676
9009
1237
6782
1.2. So sánh:
Để so sánh các số trong phạm vi 10000 hay 100000, chúng ta cần xem xét các chữ số ở hàng nghìn, hàng trăm, hàng chục và hàng đơn vị của mỗi số. Bắt đầu bằng cách so sánh các chữ số ở hàng nghìn của hai số. Số nào có chữ số ở hàng nghìn lớn hơn thì số đó lớn hơn. Nếu hai số có cùng chữ số ở hàng nghìn, tiếp tục so sánh các chữ số ở hàng trăm của hai số. Số nào có chữ số ở hàng trăm lớn hơn thì số đó lớn hơn. Nếu hai số có cùng chữ số ở hàng trăm, tiếp tục so sánh các chữ số ở hàng chục của hai số. Số nào có chữ số ở hàng chục lớn hơn thì số đó lớn hơn. Nếu hai số có cùng chữ số ở hàng chục, cuối cùng so sánh các chữ số ở hàng đơn vị của hai số. Số nào có chữ số ở hàng đơn vị lớn hơn thì số đó lớn hơn. Nếu hai số có cùng tất cả các chữ số, thì hai số bằng nhau.
* Bài tập
– Bài 1:
So sánh 1234 và 2345.
So sánh 6789 và 9876.
So sánh 10000 và 9999.
So sánh 4567 và 7654.
So sánh 3456 và 3456.
Đáp án:
1234 < 2345
6789 < 9876
10000 > 9999
4567 < 7654
3456 = 3456
– Bài 2: So sánh hai số 5678 và 8765.
Lời giải: Để so sánh hai số, ta có thể so sánh từng chữ số của chúng theo thứ tự từ trái sang phải. Ta thấy rằng chữ số hàng nghìn của 5678 là 5, nhỏ hơn chữ số hàng nghìn của 8765 là 8. Do đó, ta có thể kết luận ngay rằng 5678 < 8765.
1.3. Phép cộng, trừ:
Phép cộng, trừ các số trong phạm vi 10000, 100000 là một chủ đề quan trọng trong toán học lớp 4 và 5. Để thực hiện phép cộng, trừ các số này, chúng ta cần nhớ các quy tắc sau:
– Phép cộng, trừ các số có cùng số chữ số: thực hiện phép cộng, trừ từ phải sang trái, theo từng hàng đơn vị, chục, trăm, nghìn. Nếu có nhớ, cộng thêm vào hàng kế tiếp.
– Phép cộng, trừ các số có số chữ số khác nhau: bổ sung các số 0 vào bên trái của số có ít chữ số cho đến khi hai số có cùng số chữ số, rồi thực hiện như trên.
– Khi thực hiện phép cộng, trừ các số trong phạm vi 10000, 100000, cần kiểm tra kết quả bằng cách dùng tính chất giao hoán và kết hợp của phép cộng hoặc dùng quan hệ nghịch đảo giữa phép cộng và phép trừ.
Ví dụ:
– Phép cộng: 2345 + 6789 = 9134
Ta thực hiện như sau:
2345
+ 6789
——
9134
Kiểm tra: 9134 – 2345 = 6789
– Phép trừ: 54321 – 8765 = 45556
Ta thực hiện như sau:
54321
– 08765
——
45556
Kiểm tra: 45556 + 8765 = 54321
* Bài tập:
– Bài 1: Tính tổng các số sau:
a) 1234 + 5678
b) 34567 + 65432
c) 7890 + 210
d) 9999 + 1
Lời giải:
a) 1234 + 5678 = 6912
b) 34567 + 65432 = 99999
c) 7890 + 210 = 8100
d) 9999 + 1 = 10000
– Bài 2: Tính hiệu các số sau:
a) 8765 – 4321
b) 54321 – 12345
c) 10000 – 9999
d) 50000 – 25000
Lời giải:
a) 8765 – 4321 = 4444
b) 54321 – 12345 = 41976
c) 10000 – 9999 = 1
d) 50000 – 25000 = 25000
– Bài 3: Đặt tính rồi tính:
a) (1234 + 5678) – (4321 + 8765)
b) (34567 + 65432) – (54321 + 12345)
c) (7890 + 210) – (9999 + 1)
d) (9999 + 1) – (8765 + 4321)
Lời giải:
a) (1234 + 5678) – (4321 + 8765)
= (6912) – (13086)
= -6174
b) (34567 + 65432) – (54321 + 12345)
= (99999) – (66666)
= 33333
c) (7890 + 210) – (9999 + 1)
= (8100) – (10000)
= -1900
d) (9999 + 1) – (8765 + 4321)
= (10000) – (13086)
= -3086
1.4. Phép nhân, chia:
– Học cách đọc, viết, so sánh các số trong phạm vi 10000, 100000. Các em cần nhớ rằng mỗi số có thể được biểu diễn bằng cách ghép các chữ số từ hàng đơn vị, hàng chục, hàng trăm, hàng nghìn đến hàng chục nghìn. Ví dụ: số 12345 có thể được viết là 1 x 10000 + 2 x 1000 + 3 x 100 + 4 x 10 + 5 x 1. Khi so sánh hai số trong phạm vi này, các em cần xét từ hàng cao nhất đến hàng thấp nhất để xem số nào lớn hơn hoặc nhỏ hơn.
– Học cách thực hiện phép nhân các số trong phạm vi 10000, 100000 với một số có một chữ số hoặc hai chữ số. Cần nhớ rằng khi nhân một số có nhiều chữ số với một số có một chữ số hoặc hai chữ số, ta có thể áp dụng quy tắc nhân theo từng hàng và cộng lại kết quả.
– Học cách thực hiện phép chia các số trong phạm vi 10000, 100000 cho một số có một chữ số hoặc hai chữ số. Khi chia một số có nhiều chữ số cho một số có một chữ số hoặc hai chữ số, ta có thể áp dụng quy tắc chia theo từng hàng và lấy dư.
* Bài tập:
– Bài 1: Tính 12345 x 12
Lời giải
12345 x 12 = (12345 x 10) + (12345 x 2)
= (1 x 10 x 10000) + (2 x 10 x 1000) + (3 x 10 x 100) + (4 x 10 x 10) + (5 x 10 x 1)
+ (1 x 2 x 10000) + (2 x 2 x 1000) + (3 x 2 x 100) + (4 x 2 x 10) + (5 x 2 x 1)
= (1 + 2) x 10000 + (2 + 4) x 1000 + (3 + 6) x 100 + (4 +8) x10 + (5 +10) x1
= (3) x 10000 + (6) x1000 + (9) x100 + (12) x10 + (15) x1
= (3) x10000 + (6) x1000 + (9) x100 + (1×10+2×10) +(1×1+5×1)
= (3) x10000 +(6)x1000 +(9)x100 +(3)x10 +(6)x1
=30000+6000+900+30+6
=148176
– Bài 2: Tính thương và số dư của phép chia:12345 :12
Lời giải:
12345 :12 = ?
Ta bắt đầu từ hàng cao nhất của số bị chia là hàng nghìn. Ta thấy rằng:
– Số bị chia có hàng nghìn là:12
– Số bị chia có hàng trăm là:34
– Số bị chia có hàng đơn vị là:5
Ta lấy hai chữ số đầu tiên của số bị chia là:12 và so sánh với số chia là:12. Ta thấy rằng: 12 :12 =1. Vậy ta ghi số 1 vào hàng nghìn của thương.
Tiếp theo, ta lấy số dư của phép chia 12 :12 là 0 và nối với chữ số tiếp theo của số bị chia là 3. Ta được số mới là:03. Ta so sánh số này với số chia là:12. Ta thấy rằng: 03 < 12. Vậy ta ghi số 0 vào hàng trăm của thương.
Tiếp theo, ta lấy số dư của phép chia 03 :12 là 3 và nối với chữ số tiếp theo của số bị chia là 4. Ta được số mới là:34. Ta so sánh số này với số chia là:12. Ta thấy rằng: 34 :12 =2 (dư 10). Vậy ta ghi số 2 vào hàng chục của thương và lấy số dư là 10.
Cuối cùng, ta lấy số dư của phép chia 34 :12 là 10 và nối với chữ số cuối cùng của số bị chia là 5. Ta được số mới là:105. Ta so sánh số này với số chia là:12. Ta thấy rằng: 105 :12 =8 (dư 9). Vậy ta ghi số 8 vào hàng đơn vị của thương và lấy số dư là 9.
Vậy kết quả của phép chia là:
12345 :12 =1028 (dư 9)
1.5. Tìm thành phần chưa biết của phép tính:
Để tìm được thành phần chưa biết, ta cần hiểu ý nghĩa của các dấu bằng, cộng, trừ, nhân và chia, cũng như cách sử dụng các phép biến đổi đẳng thức. Ta cũng cần biết cách đặt tính và làm tính chính xác, cũng như kiểm tra kết quả bằng cách thực hiện phép tính ngược lại.
* Bài tập
– Bài 1: Tìm x biết: x + 3456 = 7890
Lời giải:
Có thể suy ra x bằng cách trừ 3456 cho hai vế của phép tính, ta được: x = 7890 – 3456 = 4434
Có thể kiểm tra kết quả bằng cách thực hiện phép tính ngược lại: 4434 + 3456 = 7890
– Bài 2: Tìm y biết: 1234 – y = 567
Lời giải:
Ta có thể suy ra y bằng cách cộng 567 cho hai vế của phép tính, ta được: y = 1234 – 567 = 667
Ta có thể kiểm tra kết quả bằng cách thực hiện phép tính ngược lại: 1234 – 667 = 567
– Bài 3: Tìm z biết: z x 12 = 9600
Lời giải:
Có thể suy ra z bằng cách chia hai vế của phép tính cho 12, ta được: z = 9600 / 12 = 800
Kiểm tra kết quả bằng cách thực hiện phép tính ngược lại: 800 x 12 = 9600
1.6. Tính biểu thức:
Để tính giá trị của biểu thức trong phạm vi 10000, 100000, chúng ta cần nhớ các quy tắc sau:
– Thực hiện các phép tính trong dấu ngoặc đơn trước, sau đó thực hiện các phép tính ngoài dấu ngoặc đơn.
– Thực hiện các phép nhân và chia trước, sau đó thực hiện các phép cộng và trừ.
– Nếu có nhiều phép nhân và chia liên tiếp, thực hiện từ trái sang phải.
– Nếu có nhiều phép cộng và trừ liên tiếp, thực hiện từ trái sang phải.
* Bài tập: Tính giá trị của biểu thức 3 x (4 + 5) – 6 : 2 + 7
Lời giải:
Bước 1: Thực hiện các phép tính trong dấu ngoặc đơn trước.
3 x (4 + 5) – 6 : 2 + 7 = 3 x 9 – 6 : 2 + 7
Bước 2: Thực hiện các phép nhân và chia trước.
3 x 9 – 6 : 2 + 7 = 27 – 3 + 7
Bước 3: Thực hiện các phép cộng và trừ.
27 – 3 + 7 = 31
Đáp số: Biểu thức có giá trị là 31.
2. Giải toán có lời văn:
* Dạng toán về hơn kém số đơn vị:
Bài 1: Một lớp học có 35 học sinh. Số học sinh nam nhiều hơn số học sinh nữ 3 em. Hỏi lớp học đó có bao nhiêu học sinh nam và bao nhiêu học sinh nữ?
Lời giải:
– Để giải bài toán này, ta cần tìm hai số x và y sao cho x + y = 35 và x – y = 3.
– Ta có thể dùng phương pháp cộng hai vế của hai phương trình để tìm x. Ta được: x + y + x – y = 35 + 3, hay 2x = 38, hay x = 19.
– Vậy số học sinh nam là 19 em. Để tìm số học sinh nữ, ta dùng phương pháp trừ hai vế của hai phương trình. Ta được: x + y – (x – y) = 35 – 3, hay 2y = 32, hay y = 16.
– Vậy số học sinh nữ là 16 em.
Đáp án: Lớp học đó có 19 học sinh nam và 16 học sinh nữ.
Bài 2: Cuộn dây đỏ dài 1456m. Cuộn dây xanh dài hơn cuộn dây xanh 598m. Hỏi cả 2 cuộn dây dài bao nhiêu mét?
Lời giải:
Để giải chi tiết bài tập này, ta có thể áp dụng quy tắc cộng hai số tự nhiên. Ta biết rằng cuộn dây đỏ dài 1456m, và cuộn dây xanh dài hơn cuộn dây đỏ 598m. Do đó, ta có thể viết phép tính như sau:
Cuộn dây đỏ + 598m = Cuộn dây xanh
Thực hiện cộng hai số từ phải sang trái, nhớ số nếu có:
6 + 8 = 14, ghi 4, nhớ 1
5 + 9 + 1 = 15, ghi 5, nhớ 1
4 + 5 + 1 = 10, ghi 0, nhớ 1
1 + 0 + 1 = 2, ghi 2
Vậy cuộn dây xanh dài là 2054m.
Để tính tổng độ dài của cả hai cuộn dây, ta cộng hai số đã biết:
Cuộn dây đỏ + Cuộn dây xanh = Tổng độ dài
Thực hiện cộng hai số từ phải sang trái, nhớ số nếu có:
6 + 4 = 10, ghi 0, nhớ 1
5 + 5 + 1 = 11, ghi 1, nhớ 1
4 + 0 + 1 = 5, ghi 5
2 + 0 = 2, ghi 2
Vậy tổng độ dài của cả hai cuộn dây là 3510m.
* Dạng toán về gấp, kém số lần:
Bài 1: Mảnh vải trắng dài 1569m, mảnh vải đen dài gấp 3 lần mảnh vải trắng. Hỏi cả 2 mảnh vải dài bao nhiêu mét?
Lời giải:
– Gọi x là độ dài của mảnh vải trắng, y là độ dài của mảnh vải đen.
– Theo đề bài, ta có x = 1569m và y = 3x.
– Thay x vào y, ta được y = 3 × 1569 = 4707m.
Vậy cả hai mảnh vải dài tổng cộng x + y = 1569 + 4707 = 6276m.
Bài 2: Một chiếc xe máy có giá 24 triệu đồng. Giá của chiếc xe máy này gấp 8 lần giá của một chiếc xe đạp. Hỏi giá của một chiếc xe đạp là bao nhiêu?
Lời giải:
– Số đã biết là giá của chiếc xe máy là 24 triệu đồng. Số cần tìm là giá của một chiếc xe đạp.
– Phương trình toán học là 24 = 8 x (giá của một chiếc xe đạp).
Giải phương trình ta được: giá của một chiếc xe đạp = 24 / 8 = 3 (triệu đồng).
– Kiểm tra lại kết quả ta thấy: 24 = 8 x 3 (triệu đồng) => đúng.
Đáp án là: Giá của một chiếc xe đạp là 3 triệu đồng.
* Dạng tìm một trong các phần bằng nhau của một số:
Bài tập: Cuộn dây xanh dài 9366m. Cuộn dây vàng dài bằng 1/3 cuộn dây xanh. Hỏi cả 2 cuộn dây dài bao nhiêu mét?
Lời giải:
– Gọi x là độ dài của cuộn dây vàng. Vì cuộn dây vàng dài bằng 1/3 cuộn dây xanh, nên ta có phương trình: x = 1/3 * 9366
– Giải phương trình, ta được: x = 3122
– Vậy độ dài của cuộn dây vàng là 3122m.
– Để tìm độ dài của cả hai cuộn dây, ta cộng độ dài của cuộn dây xanh và cuộn dây vàng lại: 9366 + 3122 = 12488
Vậy độ dài của cả hai cuộn dây là 12488m.
* Dạng toán liên quan đến rút đơn vị:
Bài 1: 3 hàng có 396 cây. Hỏi 5 hàng có bao nhiêu cây?
Lời giải:
Để giải bài tập này, ta có thể sử dụng quy tắc ba số gồm hai tỉ lệ. Quy tắc này cho biết nếu ba số a, b, c gồm hai tỉ lệ, tức là a/b = c/b, thì ta có thể tìm được số c bằng cách nhân a với b rồi chia cho b. Trong bài toán này, ta có ba số là số hàng (a), số cây trên mỗi hàng (b) và tổng số cây (c). Ta biết rằng số cây trên mỗi hàng là không đổi, nên ta có thể áp dụng quy tắc ba số gồm hai tỉ lệ.
Ta có:
3 hàng có 396 cây
5 hàng có bao nhiêu cây?
Ta đặt x là số cây của 5 hàng. Ta có:
3/396 = 5/x
Nhân cả hai vế của phương trình với x rồi chia cho 3, ta được:
x = (5 x 396)/3
x = 660
Vậy 5 hàng có 660 cây.
Bài 2: 24 cái bát xếp vào 4 hộp. Hỏi có 42 cái bát xếp vào được bao nhiêu hộp như thế?
Lời giải
Đây là một bài toán về tỉ lệ thức. Ta có thể viết tỉ lệ thức như sau:
24 cái bát : 4 hộp = 42 cái bát : x hộp
Từ đó, ta có thể giải ra x bằng cách nhân chéo:
24x = 4 x 42
x = (4 x 42) / 24
x = 7
Vậy, có 42 cái bát xếp vào được 7 hộp như thế.
3. Kiến thức về Hình học:
* Điểm ở giữa – trung điểm của đoạn thẳng:
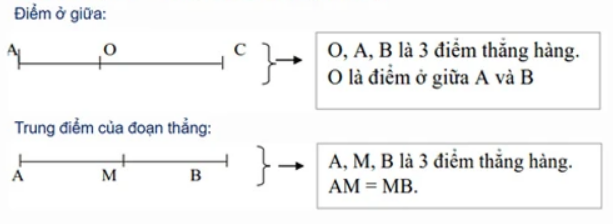
* Hình tròn, tâm, bán kính, đường kính:
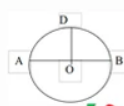
Hình tròn tâm O
– Đường kính AB đi qua O, có giới hạn bởi vành tròn A; B.
– Bán kính OA = OB = ½ AB.
– Bán kính bằng nửa đường kính: từ điểm O ra vành tròn A, B, D.
* Diện tích của 1 hình:
Bề mặt bên trong của 1 hình nào đó chính là diện tích của hình đó.
* Đơn vị đo diện tích: cm
Xăng ti mét vuông là diện tích của 1 hình vuông có cạnh 1cm.
* Diện tích hình chữ nhật:
Muốn tính diện tích hình chữ nhật, ta lấy chiều dài nhân với chiều rộng (cùng đơn vị đo).
* Diện tích hình vuông:
Tính diện tích hình vuông = cạnh × cạnh.
Bài tập:
– Bài 1: Cho một hình vuông có cạnh bằng 5 cm. Tính chu vi và diện tích của hình vuông đó.
Lời giải:
Chu vi của hình vuông là tổng độ dài các cạnh, tức là:
Chu vi = 5 cm + 5 cm + 5 cm + 5 cm = 20 cm
Diện tích của hình vuông là tích của độ dài hai cạnh liền kề, tức là:
Diện tích = 5 cm x 5 cm = 25 cm2
Vậy, chu vi và diện tích của hình vuông có cạnh bằng 5 cm là 20 cm và 25 cm2, tương ứng.
– Bài 2: Cho một hình chữ nhật có chiều dài bằng 8 cm và chiều rộng bằng 4 cm. Tính chu vi và diện tích của hình chữ nhật đó.
Lời giải
Chu vi của hình chữ nhật là (8 + 4) x 2 = 24 cm.
Diện tích của hình chữ nhật là 8 x 4 = 32 cm2.




