Tìm m để hai đường thẳng song song, cắt nhau, trùng nhau hoặc vuông góc với nhau

1. Lý thuyết:

Hai đường thẳng có nhiều tính chất và mối quan hệ khác nhau khi chúng gặp nhau trong không gian hình học. Khi hai đường thẳng cắt nhau, điểm chung của chúng được gọi là giao điểm. Điểm này là điểm duy nhất mà hai đường thẳng đó chia sẻ với nhau. Nếu hai đường thẳng không có điểm chung nào, chúng được xem là song song với nhau.

Một trường hợp đặc biệt là khi hai đường thẳng vuông góc với nhau. Điều này có nghĩa là góc tạo ra bởi hai đường thẳng là góc vuông, tức là 90 độ. Để xác định hai đường thẳng có vuông góc với nhau hay không, ta sử dụng chỉ số a x a’ = -1, với a và a’ là hệ số góc của hai đường thẳng tương ứng. Khi tích của hai hệ số góc là -1, điều này chứng tỏ chúng vuông góc.

Ngoài ra, hai đường thẳng còn có thể trùng nhau hoặc không. Trường hợp hai đường thẳng trùng nhau xảy ra khi cả hai đều có hệ số góc và hệ số góc cộng hưởng bằng nhau (a = a’ và b = b’). Trường hợp không trùng nhau diễn ra khi hệ số góc của hai đường thẳng không bằng nhau (a ≠ a’).

Những tính chất này giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các đường thẳng trong không gian hình học và cách chúng tương tác với nhau.

2. Tìm m để hai đường thẳng song song, cắt nhau, trùng nhau hoặc vuông góc với nhau:

+ Cho hai đường thẳng d: y = ax + b và d’: y = a’x + b

– Hai đường thẳng cắt nhau (d cắt d’) khi a ≠ a′

– Hai đường thẳng song song với nhau (d // d’) khi a=a′ và b≠b′

– Hai đường thẳng vuông góc (d⊥d’) khi a.a’

– Hai đường thẳng trùng nhau khi a = a′ và b = b′

+ Nếu bài toán cho 2 hàm số bậc nhất y = ax + b và y = a’x + b’ thì phải thêm điều kiện a ≠ 0,a′ ≠ 0

Bài 1: Cho hai hàm số y = kx + m -2 và y = (5 – k).x + (4 – m). Tìm m, k để đồ thị của hai hàm số:

a, Trùng nhau

b, Song song với nhau

c, Cắt nhau

Lời giải:

Để hàm số y = kx + m – 2 là hàm số bậc nhất khi k ≠0

Để hàm số y = (5 – k)x + (4 – m) là hàm số bậc nhất khi 5− k ≠0⇔ k ≠5

a, Để đồ thị của hai hàm số trùng nhau ⇔{k=5−k; m−2=4−m ⇔ {2k=5; 2m =6 ⇔ {k =5/ 2(t/m) ; m=3(t/m)

Vậy với k=5/2;m=3 thì đồ thị của hai hàm số trùng nhau

b, Để đồ thị của hai hàm số song song với nhau ⇔{k=5−k; m−2≠4−m ⇔ {k = 5/ 2; m≠3

Vậy với k=5/2;m≠3 thì đồ thị của hai hàm số song song với nhau

c, Để đồ thị của hai hàm số cắt nhau ⇔k ≠ 5−m⇔ 2k ≠ 5⇔ k ≠ 5/2

Vậy với k ≠ 5/2 thì hai đồ thị hàm số cắt nhau

Bài 2: Cho hàm số y = (2m – 3)x + m – 5. Tìm m để đồ thị hàm số:

a, Tạo với 2 trục tọa độ một tam giác vuông cân

b, Cắt đường thẳng y = 3x – 4 tại một điểm trên Oy

c, Cắt đường thẳng y = -x – 3 tại một điểm trên Ox

Lời giải:

Để hàm số là hàm số bậc nhất ⇔ 2m−3 ≠0⇔ m≠ 3/2

Gọi giao điểm của hàm số với trục Ox là A. Tọa độ của điểm A là A(5−m/2m−3;0)

Độ dài của đoạn OA=|5m/2m−3|

Gọi giao điểm của hàm số với trục Oy là B. Tọa độ của điểm B là B(0;m−5)

Độ dài của đoạn OB=|M−5|

Ta có tam giác OAB là tam giác vuông tại A

Để tam giác OAB là tam giác vuông cân ⇔|5−m/2m−3|=|m−5|⇔[m=1 hoặc m=2(t/m)

Vậy với m = 1 hoặc m = 2 thì đồ thị hàm số tạo với hai trục tọa độ tam giác vuông cân

b, Gọi A là điểm đồ thị hàm số cắt đường thẳng y = 3x – 4 tại một điểm trên trục Oy (trục tung) ⇒ A(0;b)

Thay tọa độ điểm A vào đồ thị hàm số y = 3x – 4 ta có b = 4

Điểm A(0; 4) thuộc đồ thị hàm số y = (2m – 3)x + m – 5 nên ta có

4=(2m−3).0+m−5⇔m−5=4⇔m=9(t/m)

Vậy với m = 9 thì đồ thị hàm số cắt đường thẳng y = 3x – 4 tại một điểm trên trục tung

c, Gọi B là điểm đồ thị hàm số cắt đường thẳng y = – x – 3 tại một điểm trên trục Ox (trục hoành) ⇒B(a;0)

Thay tọa độ điểm B vào đồ thị hàm số y = – x – 3 ta có a = – 3

Điểm B(-3; 0) thuộc đồ thị hàm số y = -x – 3 nên ta có:

0=(−3)(2m−3)+ m −5⇔−5m +4 = 0 ⇔ m =4/5 (t/m)

Vậy với m = 4/5 thì đồ thị hàm số cắt đường thẳng y = -x – 3 tại một điểm trên trục hoành

Bài 3: Cho hai đường thẳng (d1): y = (m + 1)x + 2 và (d2): y = 2x + 1. Tìm m để hai đường thẳng cắt nhau tại một điểm có hoành độ và tung độ trái dấu

Lời giải:

Để hai đường thẳng cắt nhau thì m+1≠2 ⇔ m≠1

Phương trình hoành độ giao điểm:

(m+1)x+2 = 2x+1

⇔mx + x + 2 = 2x+1

⇔x(m+1−2)=−1

⇔x(m−1)=−1

⇒x=−1/m−1

Với x=−1/m−1 ⇒y=2.(−1/m−1)+1=m−3/m−1

Để hoành độ và tung độ trái dấu thì x.y < 0

⇔−1/m−1.m−3/m−1<0⇔3−m(m−1)^2<0 (tử và mẫu trái dấu)

Mà (m−1)^2 ≥ 0∀ m≠1 ⇒ 3−m<0 ⇔ m>3

Vậy với m > 3 thì hai đường thẳng cắt nhau tại một điểm có hoành độ và tung độ trái dấu

Bài 4: Tìm m để đồ thị của hàm số y = (m – 2)x + m + 3 và các đồ thị của các hàm số y = -x + 2 và y = 2x – 1 đồng quy

Lời giải:

Gọi A là giao điểm của đồ thị hàm số y = -x + 2 và y = 2x – 1. Khi đó tọa độ của điểm A là nghiệm của hệ phương trình: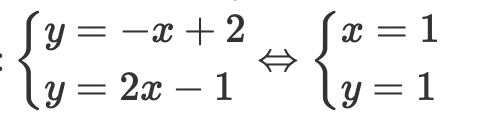 

Vậy A(1; 1)

Ba đường thẳng đồng quy nên đồ thị hàm số y = (m – 2)x + m + 3 đi qua điểm A(1; 1)

Thay tọa độ điểm A vào phương trình ta có: 1 = 1.(m – 2) + m + 3 hay m = 0

Vậy với m = 0 thì ba đường thẳng đồng quy

Bài 1: Cho hàm số y = 2x + 3k và y = (2m + 1)x + 2l – 3. Tìm điều kiện của m và k để đồ thị của hai hàm số là:

a, Hai đường thẳng cắt nhau

b, Hai đường thẳng song song với nhau

c, Hai đường thẳng trùng nhau

Bài 2: Cho hàm số y = mx + 4 và y = (2m – 3)x – 2. Tìm m để đồ thị của hai hàm số đã cho là:

a, Hai đường thẳng song song với nhau

b, Hai đường thẳng cắt nhau

c, Hai đường thẳng trùng nhau

d, Hai đường thẳng cắt nhau tại 1 điểm trên trục tung

Bài 3: Cho hai hàm số y = 2x + m – 3 và y = 5x + 5 – 3m. Tìm m để đồ thị của hai hàm số trên cắt nhau tại một điểm trên trục tung

Bài 4: Cho hai hàm số y = (m – 1)x + 3 và y = (3 – m)x + 1

a, Với giá trị nào của m thì đồ thị của hai hàm só là hai đường thẳng song song với nhau

b, Với giá trị nào của m thì đồ thị của 2 hàm số là hai đường thẳng cắt nhau

Bài 5: Cho hàm số y = mx – 2 (m khác 0). Xác định giá trị của m để đồ thị hàm số cắt hai trục tọa độ tạo thành tam giác có diện tích bằng 1.

Bài 6: Cho hàm số y = x + m. Tìm m để đồ thị hàm số song song với đường thẳng x – y + 3 = 0

Bài 7: Tìm m để đường thẳng y = x + m² + 1 và đường thẳng y = 5 + (m – 1)x cắt nhau tại

a, Một điểm trên trục hoành

b, Một điểm trên trục tung

Bài 8: Cho hai hàm số bậc nhất y = (m – 1)x + 3 và y = (3 – m)x + 1

a, Với giá trị nào của m thì đồ thị của hai hàm số là hai đường thẳng song song với nhau

b, Với giá trị nào của m thì đồ thị của hai hàm số là hai đường thẳng cắt nhau

Bài 9: Cho đường thẳng (d1): y = x + 2 và đường thẳng (d2): y = -2x + 2

a, Tìm tọa độ giao điểm của (d1) và (d2) bằng phép tính

b, Gọi giao điểm của (d1) và (d2) với trục Ox lần lượt là A và B. Tính diện tích và chu vi của tam giác ABC

Bài 10: Cho hàm số y = (2m – 1)x + n. Tìm m và n để đồ thị hàm số trên song song với đường thẳng y = 2x và đi qua A (1; 2)