Hình chiếu của một điểm lên đường thẳng, mặt phẳng là điểm giao nhau giữa đường thẳng, mặt phẳng với đường thẳng nối điểm đó với một điểm thuộc đường thẳng, mặt phẳng sao cho đường thẳng đó vuông góc với đường thẳng, mặt phẳng. Hãy xem bài viết dưới đây.
Mục lục bài viết
1. Hình chiếu của một điểm trên một đường thẳng bằng đường vuông góc:
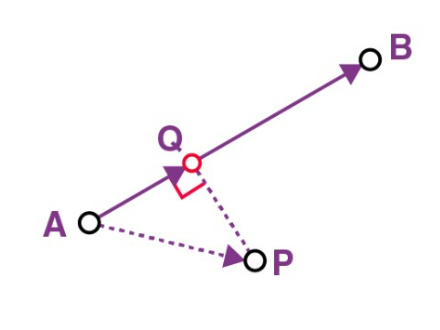
Xét đường thẳng AB và một điểm P. Từ P trên AB cắt đường thẳng PQ vuông góc với AB tại Q. Điểm Q này được gọi là hình chiếu của P lên đường thẳng AB.
2. Hình chiếu của một điểm trên một mặt phẳng:
2.1. Bằng phương pháp Monge:
* Phương pháp chiếu của Monge
Các phần tử cơ bản của mặt phẳng Euclide sẽ được ký hiệu như sau:
– điểm – chữ cái Latinh viết hoa (A, B, C, D,…)
– dòng – chữ cái Latinh viết thường (a, b, c, d,…)
– máy bay – chữ cái Hy Lạp in hoa (Α, Β, Γ, Δ,…).
* Hình chiếu của một điểm
– Cho hai mặt phẳng vuông góc Π1 và Π2 trong không gian cắt nhau tại đường thẳng x.
– Mặt phẳng Π1 nằm ngang và được gọi là mặt phẳng chiếu thứ nhất hoặc mặt phẳng chiếu ngang hoặc mặt phẳng nền.
– Mặt phẳng Π2 thẳng đứng và được gọi là mặt phẳng chiếu thứ 2 hay mặt phẳng chiếu thẳng đứng hay mặt phẳng chính diện.
– Đường giao nhau x được gọi là đường đất hoặc đường tham chiếu.
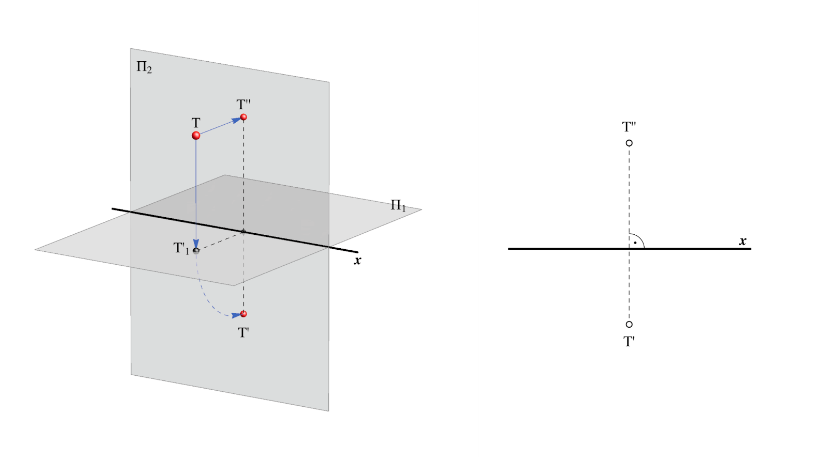
– Cho T là một điểm tùy ý trong không gian. Hình chiếu trực giao của điểm T lên mặt phẳng Π1 gọi là hình chiếu thứ nhất hay hình chiếu ngang của điểm T và ký hiệu là T’1.
– Hình chiếu trực giao của điểm T lên mặt phẳng Π2 gọi là hình chiếu thứ 2 hay hình chiếu thẳng đứng của điểm T và ký hiệu là T”.
– Bây giờ chúng ta quay mặt phẳng Π1 quanh đường giao nhau x ngược chiều kim đồng hồ một góc 90o.
Trong phép quay này, điểm T’1 biến đổi thành điểm T’ trên mặt phẳng Π2.
Điểm T’ ∈ Π2 còn được gọi là hình chiếu thứ nhất hoặc hình chiếu ngang của điểm T.
– Sự tương ứng T —> (T’,T”) được gọi là phương pháp chiếu Monge hoặc giao thức hai hình ảnh.
Đường thẳng T’T” ∈ Π2 vuông góc với giao điểm x gọi là đường hồi quy của điểm T.
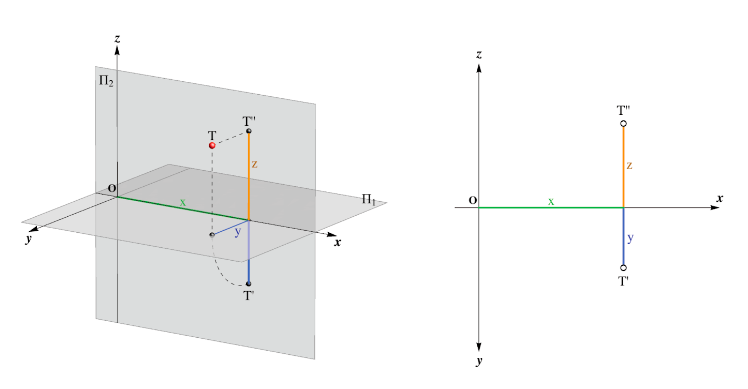
– Trong không gian, hệ tọa độ hình chữ nhật bên trái (Cartesian) sao cho trục x trùng với đường giao nhau của các mặt phẳng Π1 và Π2. Bây giờ, mọi điểm T trong không gian được xác định bởi tọa độ T(x,y,z) của nó, áp dụng công thức sau: d(T,Π1) = |z| và d(T,Π2) = |y|.
Hơn nữa
nếu z = 0 thì T nằm trong mặt phẳng Π1 (T ∈ Π1),
nếu y = 0 thì T nằm trong mặt phẳng Π2 (T ∈ Π2).
Cả hai mặt phẳng chiếu Π1 và Π2 đều chia không gian thành 2 nửa không gian và cùng nhau thành 4 góc phần tư.
Các nửa không gian được gọi là trên và dưới (trên và dưới mặt phẳng Π1), phía trước và phía sau (phía trước và phía sau mặt phẳng Π2).
Các góc phần tư được gọi là: I (mặt trước trên), II (mặt sau trên), III (lưng dưới), IV (mặt trước dưới).
Nửa không gian hoặc góc phần tư của T(x,y,z) phụ thuộc vào dấu của tọa độ y và z
Z
Từ các hình chiếu ngang và dọc của một điểm, có thể xác định được nó thuộc góc phần tư nào.
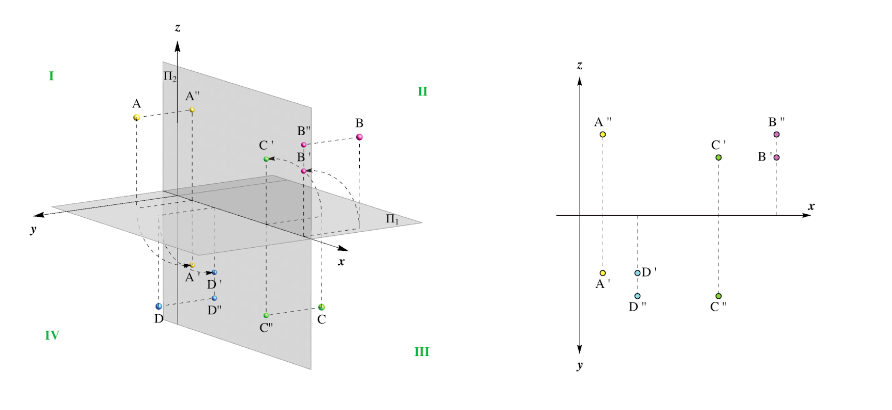
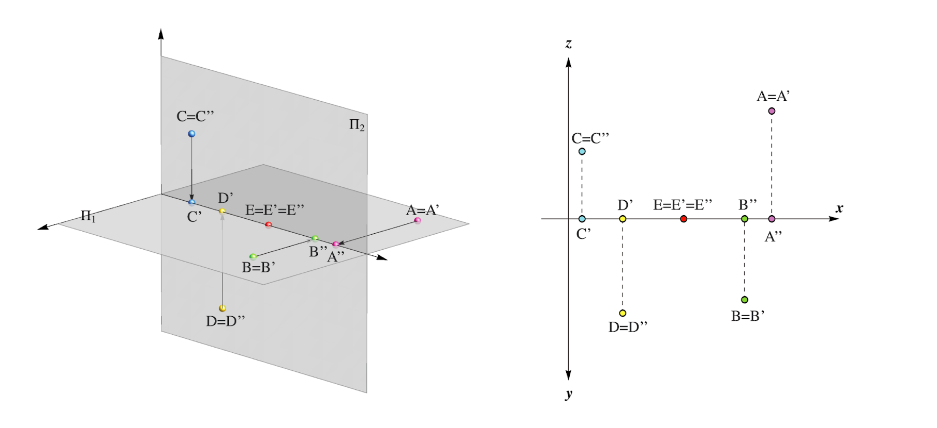
Trong hình bên dưới là một số ví dụ về các điểm trong các góc phần tư khác nhau và các hình chiếu trực giao của chúng
(A ∈ I, B ∈ II, C ∈ III, D ∈ IV).
* Điểm ở vị trí đặc biệt
Nếu một điểm nằm trên một trong các mặt phẳng chiếu thì nó sẽ trùng với hình chiếu của nó lên mặt phẳng đó, còn hình chiếu còn lại sẽ nằm trên trục x.
– Nếu T ∈ Π1 thì T’ = T và T” ∈ x, tức là hình chiếu thẳng đứng của nó nằm trên trục x.
– Nếu T ∈ Π2 thì T” = T và T’ ∈ x, tức là hình chiếu ngang của nó nằm trên trục x.
– Nếu T ∈ x thì nó trùng với các hình chiếu ngang và dọc của nó, tức là T = T’ = T” .
Trên các hình sau đây là hình chiếu của các điểm sau: A,B ∈ Π1, C,D ∈ Π2 và E ∈ x.
Hai mặt phẳng khác trong không gian có hình chiếu ngang và hình chiếu thẳng đứng ở vị trí đặc biệt là:
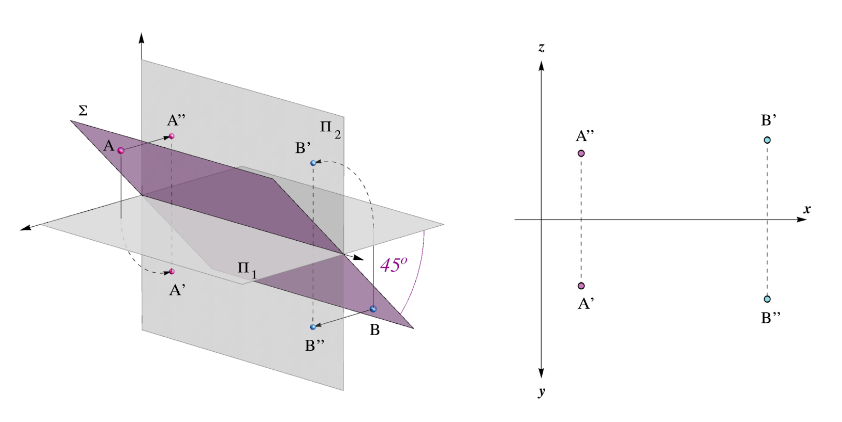
Σ – mặt phẳng đối xứng, chia đôi góc phần tư Ist và III – các hình chiếu ngang và dọc của mọi điểm đều đối xứng quanh trục x.
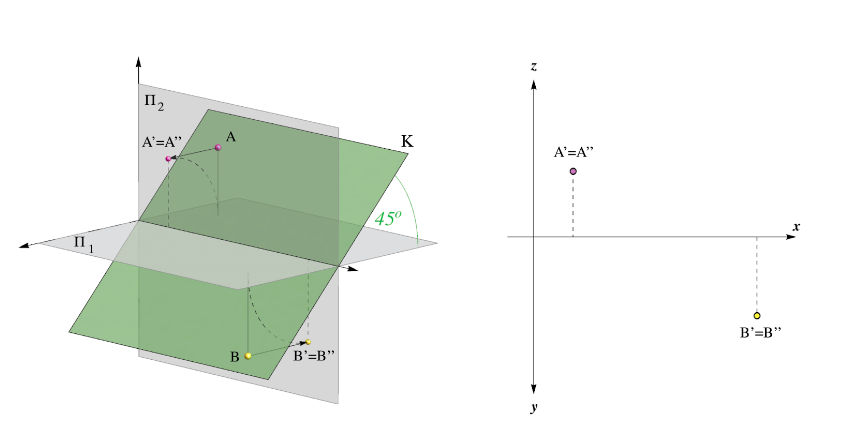
Κ – mặt phẳng trùng khớp, chia đôi góc phần tư II và IV – các hình chiếu ngang và dọc của mọi điểm đều trùng nhau.
Hình dưới đây là hình chiếu trực giao của hai điểm A,B ∈ Σ.
Hình dưới đây là hình chiếu trực giao của hai điểm A,B ∈ Κ.
2.2. Bằng phương pháp tọa độ:
Giả sử chúng ta có một điểm có tọa độ Z = [Z1, Z2, Z3] và một mặt phẳng có phương trình là:
![]() (1)
(1)
trong đó X1, X2, X3 là điểm bất kỳ trên mặt phẳng và a, b, c, d là các tham số của điểm đó. Về mặt hình học, [a, b, c] là vectơ bình thường của mặt phẳng. Nó không nhất thiết phải đơn nhất nhưng cần phải khác không. Tham số d là tọa độ X3 của giao điểm của mặt phẳng với trục X3. Trực quan:
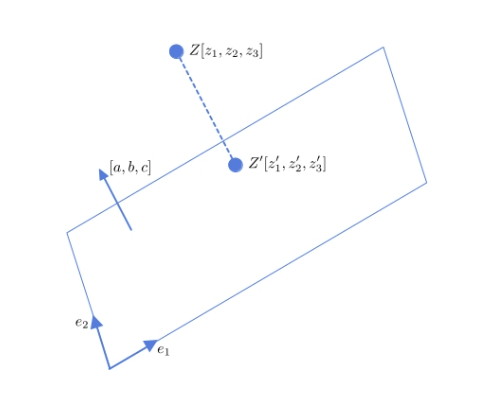
Mặt phẳng có hệ tọa độ hai chiều riêng, được xác định bởi hai vectơ đơn vị cơ sở e1 và e2.
Vì vậy, mục tiêu của chúng ta là tìm tọa độ của hình chiếu Z’ lên mặt phẳng trong hệ tọa độ được xác định bởi e1 và e2.
* Cách tìm hình chiếu một điểm
Hãy bắt đầu bằng cách chiếu Z lên mặt phẳng và tìm tọa độ trong hệ thống 3D gốc. Vì phép chiếu Z’ thuộc mặt phẳng nên tọa độ của nó phù hợp với phương trình (1):
![]() (2)
(2)
Hơn nữa, đường thẳng nối Z và Z’ vuông góc với mặt phẳng nên nó song song với vectơ pháp tuyến của mặt phẳng. Vectơ của đường thẳng là ![]() . Vì vậy, ta có:
. Vì vậy, ta có:
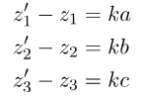 (3)
(3)
với một số thực k.
Bằng cách giải (3) cho z1, z2 và z3 và thay các biểu thức thu được vào phương trình (2), chúng ta nhận được:
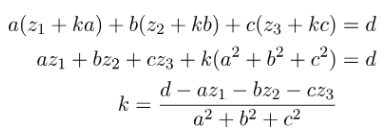
Nếu vectơ pháp tuyến cũng là vectơ đơn vị (tức là độ dài của nó bằng 1), thì mẫu số cũng là một vì nó biểu thị độ dài bình phương của vectơ.
Bằng cách thay thế k vào phương trình (2), chúng ta có thể dễ dàng tính được tọa độ:
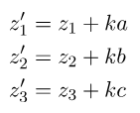
3. Hình chiếu của một đường thẳng trên mặt phẳng:
Hình chiếu trực giao của một đường thẳng lên mặt phẳng là một đường thẳng hoặc một điểm. Nếu một đường thẳng vuông góc với một mặt phẳng thì hình chiếu của nó là một điểm. Giao điểm với mặt phẳng và vectơ chỉ phương s của nó sẽ trùng với vectơ pháp tuyến N của mặt phẳng.
Nếu một đường thẳng song song với một mặt phẳng thì nó sẽ song song với hình chiếu của nó lên mặt phẳng đó. Nó trực giao với vectơ pháp tuyến của mặt phẳng.
s⊥N
s.N = 0
Hình chiếu của một đường thẳng không song song cũng không vuông góc với một mặt phẳng sẽ đi qua giao điểm B của chúng và đi qua hình chiếu A’ của bất kỳ điểm A nào của đường thẳng lên mặt phẳng, như minh họa trong hình trên.
* Ví dụ
Tìm phương trình hình chiếu của đường thẳng (x+1)/-2 = (y-1)/3 = (z+2)/4 trên mặt phẳng 2x + y + 4z = 1.
Lời giải:
Cho phương trình đường thẳng (x+1)/-2 = (y-1)/3 = (z+2)/4 = λ
Vậy x = -2λ – 1
y= 3λ + 1
z= 4λ – 2
Phương trình mặt phẳng là 2x + y +4z = 1
λ sẽ thỏa mãn phương trình của mặt phẳng.
2(-2λ-1) +3λ + 1 + 4(4λ-2) = 1
-4λ – 2 + 3λ + 1 + 16λ – 8 = 1
15λ – 10 = 0
15λ = 10
λ = 10/15 = ⅔
Thay thế λ vào x, y và z và tìm các giá trị tương ứng.
x = -2λ – 1 = -2(⅔)-1 = -7/3
y = 3λ + 1 = 3(⅔)+1 = 3
z= 4λ -2 = 4(⅔)-2 = ⅔
Tọa độ điểm B = (-7/3, 3, ⅔)
Tọa độ của A = (-1,1,-2)
Phương trình vectơ pháp tuyến N = 2i + j + 4k
Phương trình đường thẳng = (x – x0)/a = (y-y0)/b = (z-z0)/c
(x+1)/2 = (y-1)/1 = (z+2)/4 = t
Vậy x = 2t – 1
y= t + 1
z= 4t – 2
Thay x, y, z vào phương trình mặt phẳng
2(2t – 1) + (t + 1) + 4(4t – 2) = 1
21t = 10
t = 21/10
Thay thế t vào x, y, z
x = -1/21
y = 31/21
z = -2/21
Tọa độ điểm A’ = (-1/21, 31/21, -2/21)
Phương trình của đường thẳng là (x – x1)/(x2 – x1) = (y – y1)/(y2 – y1) = (z – z1)/(z2 – z1) ..(i)
(x1, y1, z1) = (-7/3, 3, ⅔)
(x2, y2, z2) = (-1/21, 31/21, -2/21)
Thay thế (x1, y1, z1) và (x2, y2, z2) vào (i)
(x + 7/3)/((-1/21) + (7/3)) = (y – 3)/((31/21) – 3) = (z – (⅔))/((- 21/2) – (⅔))
Giải chúng ta được (21x + 49)/48 = 21(y – 3)/-32 = (21z – 14)/-16 là phương trình cần tìm.




