Thiết diện là gì? Diện tích thiết diện là gì? Diện tích thiết diện của một hình hộp chữ nhật? Diện tích thiết diện của một hình trụ? Diện tích thiết diện của một hình cầu? Ví dụ về tính thiết diện? Bài tập về thiết diện?
Mục lục bài viết
1. Thiết diện là gì?
Trong hình học và khoa học, Thiết diện (hay mặt cắt) là giao điểm không rỗng của vật rắn trong không gian ba chiều với mặt phẳng hoặc mặt phẳng tương tự trong không gian nhiều chiều hơn. Cắt một vật thể thành các lát cắt sẽ tạo ra nhiều mặt cắt ngang song song.
Nếu một mặt phẳng cắt một vật rắn (một vật thể 3 chiều), thì miền chung của mặt phẳng và vật rắn đó được gọi là mặt cắt ngang của vật rắn. Mặt phẳng chứa mặt cắt ngang của vật rắn có thể được gọi là mặt phẳng cắt .
Hình dạng của mặt cắt ngang của vật rắn có thể phụ thuộc vào hướng của mặt phẳng cắt đối với vật rắn. Ví dụ, trong khi tất cả các mặt cắt ngang của một quả bóng là các đĩa, các mặt cắt ngang của một khối lập phương phụ thuộc vào cách mặt phẳng cắt liên quan đến khối lập phương. Nếu mặt phẳng cắt vuông góc với đường nối tâm hai mặt đối diện của hình lập phương thì thiết diện sẽ là hình vuông, còn nếu mặt phẳng cắt vuông góc với đường chéo của hình lập phương nối các đỉnh đối diện thì thiết diện phần có thể là một điểm, một hình tam giác hoặc một hình lục giác.
Ví dụ Cho một hình chóp bất kì (S.ABCD). Lấy điểm (M) là trung điểm của đoạn (SA). Khi đó mặt phẳng được gọi là ( (P) ) đi qua điểm ( M ) và song song với mặt phẳng đáy (ABCD) sẽ cắt hình chóp (S.ABCD). Thiết diện hay mặt cắt chính là tứ giác ( MNPQ ) với các điểm (N,P,Q ) lần lượt là trung điểm của các cạnh (SB,SC,SD)

Thiết diện của hình trụ là hình tròn, thiết diện của hình nón là hình tròn, thiết diện của quả trứng là hình elip, v.v.
Như vậy Cho hình trên là T và mặt phẳng (P) là hình đa giác (MNPQ), phần mặt phẳng của (P) nằm trong hình T được giới hạn bởi các giao tuyến sinh ra bởi (P) cắt một số mặt của T thì được gọi là thiết diện.
2. Diện tích thiết diện là gì?
Diện tích thiết diện là diện tích của hình dạng hai chiều thu được khi một vật thể ba chiều – chẳng hạn như hình trụ – được cắt vuông góc với một số trục xác định tại một điểm. Ví dụ, thiết diện của một hình trụ – khi được cắt song song với đáy của nó – là một hình tròn.
3. Diện tích thiết diện của một hình hộp chữ nhật:
Thể tích của bất kỳ hình hộp chữ nhật nào, kể cả hình lập phương, bằng diện tích đáy (chiều dài nhân chiều rộng) nhân với chiều cao: V = l × w × h.
Do đó, nếu một mặt cắt ngang song song với mặt trên hoặc mặt dưới của vật rắn, thì diện tích của mặt cắt ngang là l × w. Nếu mặt phẳng cắt song song với một trong hai tập hợp các cạnh, thì thay vào đó, diện tích mặt cắt ngang được cho bởi l × h hoặc w × h.
Nếu thiết diện không vuông góc với trục đối xứng nào thì hình tạo ra có thể là tam giác (nếu đặt qua một góc của vật rắn) hoặc thậm chí là lục giác.
Ví dụ: Tính diện tích thiết diện của mặt phẳng vuông góc với mặt đáy của hình lập phương có thể tích 27 m 3. Vì l = w = h đối với một hình lập phương nên bất kỳ cạnh nào của hình lập phương cũng phải dài 3 m (vì 3 ×3 x 3 = 27). Do đó, một mặt cắt ngang của loại được mô tả sẽ là một hình vuông có cạnh 3 m, có diện tích là 9 m 2.
4. Diện tích thiết diện của một hình trụ:
Hình trụ là một vật rắn được tạo ra bằng cách kéo dài một đường tròn trong không gian vuông góc với đường kính của nó. Diện tích hình tròn được cho bởi công thức πr 2, trong đó r là bán kính. Do đó, có thể hiểu rằng thể tích của một hình trụ sẽ là diện tích của một trong các hình tròn tạo thành đáy của nó.
Nếu mặt cắt song song với trục đối xứng, thì diện tích của mặt cắt chỉ đơn giản là một hình tròn có diện tích πr 2 . Nếu mặt phẳng cắt được chèn ở một góc khác, hình dạng được tạo ra là hình elip. Diện tích sử dụng công thức tương ứng: πab (trong đó a là khoảng cách dài nhất từ tâm của hình elip đến cạnh và b là khoảng cách ngắn nhất).
5. Diện tích thiết diện của một hình cầu:
Bất kỳ mặt phẳng lý thuyết nào được đặt qua một hình cầu sẽ dẫn đến một hình tròn (hãy suy nghĩ về điều này trong giây lát). Nếu bạn biết đường kính hoặc chu vi của hình tròn mà mặt cắt tạo thành, bạn có thể sử dụng các mối quan hệ C = 2πr và A = πr 2 để có được một giải pháp.
Ví dụ: Một chiếc máy bay được đưa thô sơ qua Trái đất rất gần Bắc Cực, loại bỏ một phần của hành tinh xung quanh 10 m. Diện tích mặt cắt ngang của lát Trái đất lạnh giá này là gì?
Vì C = 2πr = 10 m nên r = 10/2π = 1,59 m; A = πr 2 = π(1,59) 2 = 7,96 m 2 .
6. Ví dụ về tính thiết diện:
Cho hình chóp là S.ABCD có đáy hình vuông ABCD và tâm O và AB=a. Biết rằng đoạn SA vuông góc với mặt phẳng (ABCD) và đoạn thẳng SA=a√2. Mặt phẳng (P) đi qua B và vuông góc với đoạn SC. Yêu cầu Tính diện tích thiết diện của hình chóp S.ABCD được cắt bởi mặt phẳng (P)
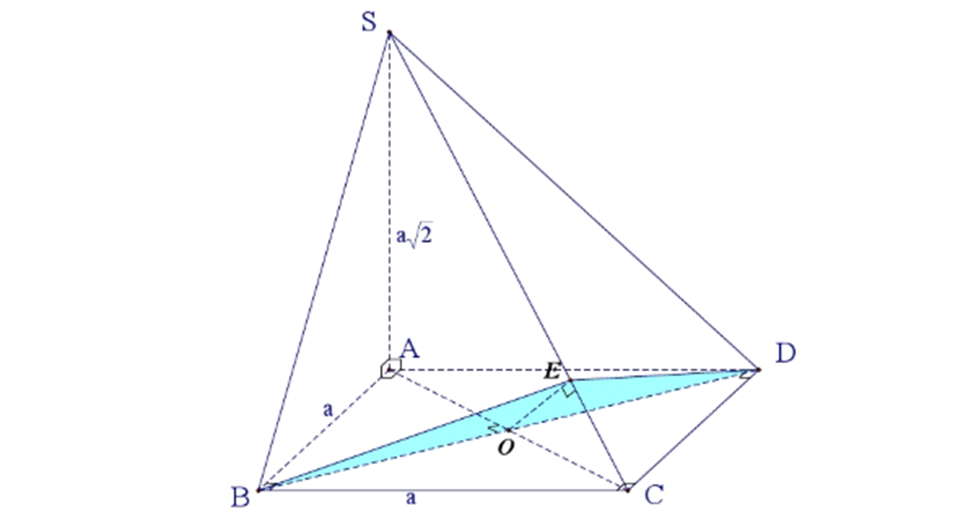
Lời giải:
Có:
SA vuông góc với (ABCD) suy ra SA vuông góc với BD
BD vuông góc với AC
⇒BD vuông góc với (SAC)
⇒BD vuông góc với SC(1)
Trong (SAC) kẻ đoạn OE vuông góc với SC(2)
Từ (1)(2)⇒(BED) vuông góc với SC
Vậy (BED) chính là mặt phẳng (P) nên thiết diện cần tìm trong bài là tam giác BED
Trong hình vuông ABCD có cạnh AB=a nên suy ra đường chéo AC = BD = a√2 (3)
Trong (SAC) tam giác SAC vuông tại điểm A.
⇒SC = √( SA2+AC2)= 2a
OC = AC / 2 = a / √2
Xét hai tam giác là Δ SAC và Δ OEC có :
Aˆ= Eˆ= 90∘
Cˆ chung
⇒Δ SAC∼Δ OEC
Vì vậy ta có :
OE / SA= OC / SC⇒ OE = (OC . SA) / SC = (a/√2 . a√2) / 2a = a / 2 (4)
Vì BD ⊥ (SAC) nên BD ⊥ EO (5)
Từ (3)(4)(5) ta có :
S (BED) = BD . EO2 =(a√2 . a/2) / 2= a2 / 2√2
Vậy diện tích thiết diện là a2 / 2√2 đơn vị diện tích
7. Bài tập về thiết diện:
1. Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng a. Gọi M,N,P lần lượt là trung điểm của SA,SB,SC. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP) và tính diện tích thiết diện đó ?
2. Cho hình lập phương ABCD. A’B’C’D’ cạnh a . Các điểm M , N , P theo thứ tự đó thuộc các cạnh BB¢ , C’D¢, DA sao cho BM= C’N = DP= a/3. Mặt phẳng (MNP) cắt đường thẳng A’ B’ tại E. Tính độ dài đoạn thẳng A’ E
3. Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh AB a = 8 , SA = SB = SC = SD = 8a . Gọi N là trung điểm cạnh SD . Tính diện tích thiết diện của hình chóp S .ABCD cắt bởi mặt phẳng ( ABN ) .
4. Cho hình chóp S. ABCD có đáy là hình vuông cạnh a , mặt bên SAB là tam giác đều, SAD = 90° . Gọi Dx là đường thẳng qua D và song song với SC . Gọi I là giao điểm của Dx và (SAB) . Tìm thiết diện của hình chóp cắt bởi mặt phẳng của ( AIC) và tính diện tích của thiết diện đó.
5. Cho hình chóp S ABCD có đáy ABCD là hình vuông, biết AB = a , SAD = 90° và tam giác SAB là tam giác đều. Gọi Dt là đường thẳng qua D và song song với SC , I là giao điểm của Dt với mặt phẳng (SAB) . Thiết diện của hình chóp S ABCD với mặt phẳng ( AIC) có diện tích là bao nhiêu.
6. Cho hình chóp SABC. Bên trong tam giác ABC lấy một điểm O bất kỳ. Từ O dựng các đường thẳng lần lượt song song với SA, SB , SC và cắt các mặt phẳng (SBC) , (SCA) , (SAB) theo thứ tự lần lượt tại A¢, B¢, C¢ . Khi đó tổng tỉ số T = OA’/ SA + OB’/ SB + OC’/ SC bằng bao nhiêu ?
7. Cho tứ diện ABCD . Điểm M là trung điểm của cạnh AC , điểm N thuộc cạnh AD sao cho: AN = 2 ND , điểm Q thuộc cạnh BC sao cho BC = 4 BQ. Gọi I là giao điểm của đường thẳng MN và mặt phẳng (BCD) , J là giao điểm của đường thẳng BD và mặt phẳng (MNQ) . Khi đó JB/ JQ + JD/ JI bằng bao nhiêu?
8. Cho hình chóp S ABCD có đáy là hình bình hành tâm O . Hai điểm M N, lần lượt nằm trên các đoạn SO SD , sao cho SM/SO= SN/SD= m/n; m, nÎ N* (m,n) = 1 . Điểm E là trung điểm của BC. Biết thiết diện của hình chóp cắt bởi mp(MNE) đi qua trung điểm cạnh SA. Giá trị m n + bằng bao nhiêu?