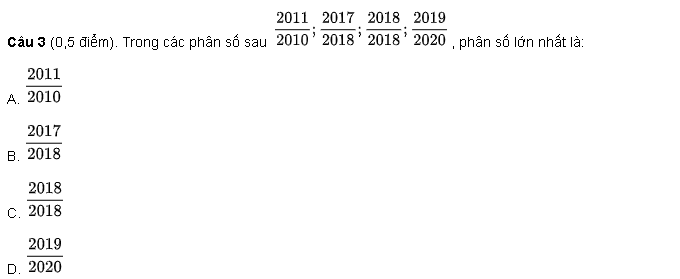Giải bài tập trang 112, 113, 114 SGK Toán 4: Rút gọn phân số là tài liệu tham khảo với lời giải chi tiết rõ ràng giúp các em học sinh dễ dàng hiểu được cách rút gọn phân số và phân số tối giản, cách rút gọn phân số trong một số trường hợp đơn giản. Sau đây mời các em cùng tham khảo chi tiết lời giải.
Mục lục bài viết
1. Lý thuyết về rút gọn phân số:
a) Cho phân số 
. Tìm phân số bằng phân số nhưng có tử số và mẫu số bé hơn.
Ta có thể làm như sau:
Ta thấy 10 và 15 đều chia hết cho 5. Theo tính chất cơ bản của phân số ta có:
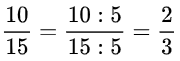
Vậy:
.
Nhận xét:
• Tử số và mẫu số của phân số 
đều bé hơn tử số và mẫu số của phân số .
• Hai phân số và bằng nhau.
Ta nói rằng: Phân số đã được rút gọn thành phân số .
Có thể rút gọn phân số để được một phân số có tử số và mẫu số bé đi mà phân số mới vẫn bằng phân số đã cho.
b) Cách rút gọn phân số
Ví dụ 1: Rút gọn phân số
.
Ta thấy: 6 và 8 đều chia hết cho 2, nên
.
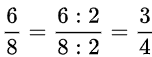3 và 4 đều không cùng chia hết cho một số tự nhiên nào lớn hơn 1, nên phân số 
không thể rút gọn được nữa. Ta nói rằng: phân số là phân số tối giản và phân số đã được rút gọn thành phân số tối giản .
Ví dụ 2: Rút gọn phân số 
.
Ta thấy: 18 và 54 đều chia hết cho 2, nên
.
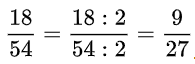9 và 27 đều chia hết cho 9, nên
.
1 và 3 đều không cùng chia hết cho số tự nhiên nào lớn hơn 1, nên
là phân số tối giản.
Vậy: 
.
Khi rút gọn phân số có thể làm như sau:
• Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
• Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
2. Bài tập toán lớp 4 trang 112:
Bài 1:
Viết số thích hợp vào ô trống:
a)
;
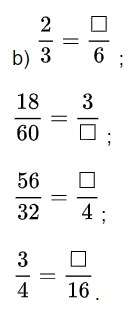
Phương pháp giải:
Áp dụng tính chất cơ bản của phân số:
– Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
– Nếu chia cả tử và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Đáp án:
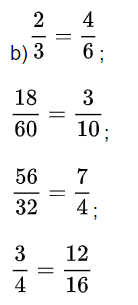
Bài 2:
Tính rồi so sánh kết quả:
a) 18 : 3 và (18 x 4) : (3 x 4)
b) 81 : 9 và (81 : 3) : (9 : 3)
Nhận xét: Nếu nhân (hoặc chia) số bị chia và số chia với (cho) cùng một số tự nhiên khác 0 thì giá trị của thương không thay đổi.
Phương pháp giải:
Biểu thức có dấu ngoặc thì tính trong ngoặc trước, ngoài ngoặc sau.
Đáp án:
a) 18 : 3 = 6
(18 x 4) : (3 x 4) = 72 : 12 = 6
Vậy kết quả của 18 : 3 và (18 x 4) : (3 x 4) bằng nhau.
b) 81 : 9 = 9
(81 : 3) : (9 : 3) = 27 : 3 = 9
Vậy kết quả của 81 : 9 và (81 : 3) : (9 : 3) bằng nhau.
Bài 3
Viết số thích hợp vào ô trống:
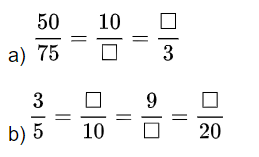
Phương pháp giải:
Áp dụng tính chất cơ bản của phân số:
– Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
– Nếu chia cả tử và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Đáp án:
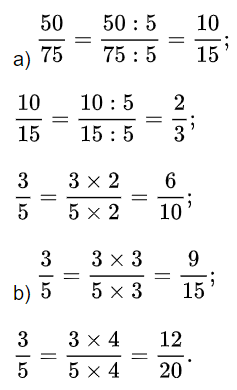
Vậy ta có kết quả như sau:
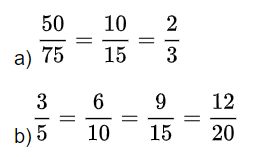
3. Bài tập toán lớp 4 trang 114:
Bài 1:
Giải Toán lớp 4 Bài 1 trang 114 SGK Toán 4 tập 2: Rút gọn các phân số:
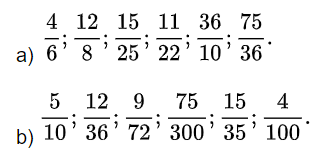
Phương pháp giải:
Cách rút gọn phân số:
– Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
– Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).
Đáp án:
Bài 2
Giải Toán lớp 4 Bài 2 trang 114 SGK Toán 4 tập 2: Trong các phân số:
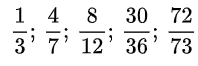
a) Phân số nào tối giản? Vì sao?
b) Phân số nào rút gọn được? Hãy rút gọn phân số đó?
Phương pháp giải:
Cách rút gọn phân số :
– Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
– Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).
Đáp án:
a) Các phân số tối giản là:
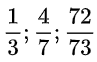
Vì tử số và mẫu số của mỗi phân số trên không cùng chia hết cho một số tự nhiên nào khác 1.
b) Các phân số rút gọn được là: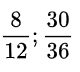 
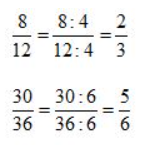
Bài 3
Giải Toán lớp 4 Bài 3 trang 114 SGK Toán 4 tập 2: Viết số thích hợp vào ô trống:
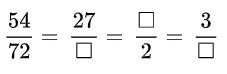
Phương pháp giải:
Cách rút gọn phân số :
– Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
– Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa)
Đáp án:
Rút gọn các phân số ta có:
Vậy ta có kết quả như sau :
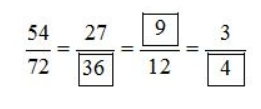
4. Các cách tìm phân số tối giản chi tiết:
Để rút gọn phân số, ta sẽ tiến hành chia cả tử và mẫu số cho cùng 1 số đảm bảo số bị khác khác 0 và 1. Ngoài ra, các em cũng có thể tối giản phân số theo các cách sau đây.
Cách 1: Sử dụng thừa số chung lớn nhất
Bước 1: Liệt kê các thừa số của cả tử và mẫu số từ nhỏ đến lớn, bao gồm cả 1 hoặc chính nó. Thừa số ở đây chính là số mà khi bạn nhân chúng với nhau sẽ được số khác, ví dụ 2 và 5 là hai thừa số của 10, vì ta có thể nhân chúng lại với nhau để có kết quả là 10.
Ví dụ, liệt kê thừa số chung của phân số 24/32:
24: 1, 2, 3, 4, 6, 8, 12, 24.
32: 1, 2, 4, 8, 16, 32.
Bước 2: Tìm thừa số chung lớn nhất (GCF) của tử và mẫu số. GCF chính là số lớn nhất mà các số có thể đều chia hết. Sau khi đã tìm và liệt kê các thừa số ở bước 1, sau đó bạn phải tìm ra GCF của hai số đó.
Chẳng hạn:
24: 1, 2, 3, 4, 6, 8, 12, 24.
32: 1, 2, 4, 8, 16, 32.
Lúc này GCF của 24 và 32 là 8, vì 8 là số lớn nhất mà cả 24 và 32 đều chia hết cho.
Bước 3: Tiến hành chia và tử và mẫu cho GCF. Sau khi đã tìm được GCF ở bước 2, ta tiến hành chia cả tử và mẫu số cho số đó để đưa chúng về phân số tối giản.
Ta có:
24/8 = 3
32/8 = 4
Lúc này phân số được rút gọn là 3/4.
Bước 4: Kiểm tra kết quả. Để chắc chắn hơn việc phân số đã được rút gọn, mọi người tiến hành kiểm tra bằng cách nhân nhân tử và mẫu số vừa rút gọn cho GCF, nếu ra kết quả phân số ban đầu thì chính xác.
Cụ thể:
3 * 8 = 24
4 * 8 = 32
Lúc này, kết quả chính là phân số ban đầu 24/32.
Cách 2: Chia liên tiếp cho một số nhỏ
Bước 1: Lựa chọn một số nhỏ. Cụ thể, ở cách rút gọn phân số này các em sẽ chọn một chữ số nhỏ như 2, 3, 4… để bắt đầu. Nhìn xem phần tử và mẫu số có chia được hết ít nhất một lần cho số mà bé đã chọn hay không.
Ví dụ, phân số 24/32, số 2 là thích hợp nhất vì cả 24 và 32 đều là số chẵn, có thể chia hết cho 2.
Bước 2: Chia cả tử và mẫu số cho số nhỏ nhất đã chọn. Sau khi đã tìm được số nhỏ nhất để chia ở bước 1, ta tiến hành chia cả tử và mẫu cho số đó.
Cụ thể:
24/2 = 12
32/2 = 16
Lúc này ta được phân số mới 12/16.
Bước 3: Lặp lại quá trình này. Nếu cả tử và mẫu đều vẫn chia tiếp được cho số nhỏ đã chọn đó, ta tiếp tục thực hiện lại bước 2. Nếu chỉ một hoặc cả 2 là số lẻ thì sẽ phải tìm số nhỏ khác và chia chúng cho số mới đó.
12/2 = 6
16/2 = 8
Phân số mới là 6/8.
Bước 4: Tiếp tục chia cả tử và mẫu cho số đó cho đến khi không thể chia thêm nữa. Ở đây nếu cả tử và mẫu số mới vẫn là số chẵn, ta tiếp tục chia tiếp cho 2 cho đến khi không thể chia thêm được nữa.
Cụ thể:
6/2 = 3
8/2 = 4
Ta được phân số mới là 3/4.
Bước 5: Hãy đảm bảo phân số mới không thể rút gọn được nữa. Có nghĩa phân số mới đó chỉ có thể chia hết cho 1 và chính nó thì đó là phân số đã được tối giản. Chẳng hạn ở phân số ¾ ta không thể chia hết được cho số nào nữa ngoài trừ nó và 1 thì phân số đã được rút gọn.
Bước 6: Kiểm tra lại kết quả. Ta sẽ nhân ¾ với 2/2 ba lần để xem có ra được kết quả là phân số ban đầu là 24/32 không nhé.
Cụ thể:
3/4 * 2/2 = 6/8
6/8 * 2/2 = 12/16
12/16 * 2/2 = 24/32.
Lưu ý: Các em đã chia 24/32 cho 3 lần 2 có nghĩa là 2 x 2 x 2 tương ứng với việc chia nó cho 8, đây chính là GCF của cả tử và mẫu. Đây là cách rút gọn phân số khá rườm rà hơn với cách 1, nhưng sẽ giúp các bé hiểu được bản chất khi thực hiện phép tính.
THAM KHẢO THÊM:
