Quy tắc hình bình hành là gì? Công thức và các dạng bài tập?

1. Tổng quan về hình bình hành:

1.1. Định nghĩa thế nào là hình bình hành:

Hình bình hành là một loại đa giác có bốn cạnh, trong đó hai cặp cạnh đối diện song song với nhau. 

Hình bình hành là một hình học quen thuộc và có nhiều ứng dụng trong thực tế. Bạn có thể tìm thấy nhiều ví dụ về hình bình hành trong kiến trúc, nghệ thuật, thiết kế và toán học.

1.2. Các tính chất của hình bình hành:

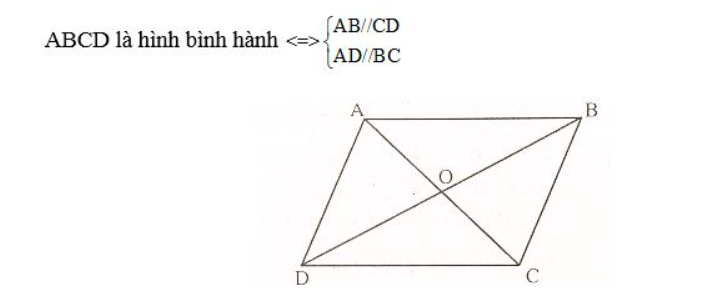
Nếu tứ giác ABCD là hình bình hành thì:

– Các cạnh đối song song và bằng nhau; AB = CD, AD = BC

– Các góc đối bằng nhau: A = C, B = D

– Hai đường chéo cắt nhau tại trung điểm của mỗi đường: OA = OC, OB = OD.

1.3. Đặc điểm nhận biết của hình bình hành:

Để nhận biết một hình bình hành, ta có thể dựa vào các dấu hiệu sau:

– Nếu một hình tứ giác có hai cặp cạnh song song, thì đó là hình bình hành.

– Nếu một hình tứ giác có hai cặp góc đối diện bằng nhau, thì đó là hình bình hành.

– Nếu một hình tứ giác có hai đường chéo chia nhau thành hai nửa bằng nhau, thì đó là hình bình hành.

– Nếu một hình tứ giác có một cặp góc kề bù, thì đó là hình bình hành.

Một số ví dụ về hình bình hành là hình vuông, hình chữ nhật và hình thoi. Tuy nhiên, không phải mọi hình bình hành đều có các tính chất của các hình đặc biệt này.

2. Quy tắc hình bình hành:

Quy tắc hình bình hành trong vật lý là một quy tắc đơn giản để xác định kết quả của hai lực tác dụng lên một vật. Quy tắc này nói rằng nếu hai lực có cùng điểm tác dụng và không cùng hướng, thì ta có thể vẽ hai vector đại diện cho hai lực đó sao cho chúng tạo thành hai cạnh liền kề của một hình bình hành. Kết quả của hai lực đó sẽ bằng với vector đường chéo của hình bình hành, có cùng điểm bắt đầu với hai vector ban đầu. Quy tắc hình bình hành có thể áp dụng cho bất kỳ số lượng lực nào, miễn là chúng có cùng điểm tác dụng. Quy tắc này giúp ta phân tích và tính toán các lực trong các trường hợp phức tạp một cách dễ dàng và trực quan.

Quy tắc hình bình hành là một quy tắc được áp dụng trong toán học và vật lý để biểu diễn tổng hai vectơ hoặc tổng hợp lực của hai lực quy đồng. Quy tắc này có thể được phát biểu như sau:

Cho hình bình hành ABCD, ta có: AB + AD = AC hoặc BC + BD = AC.

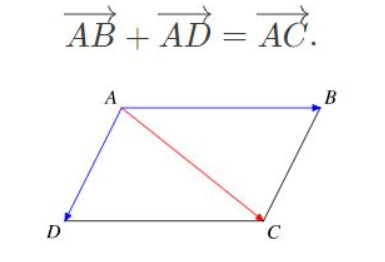
Nghĩa là: Tổng hai vectơ cạnh chung điểm đầu của một hình bình hành bằng vectơ đường chéo có cùng điểm đầu đó.

Chứng minh. Việc chứng minh dựa vào hai vectơ bằng nhau và quy tắc 3 điểm, quy tắc trừ

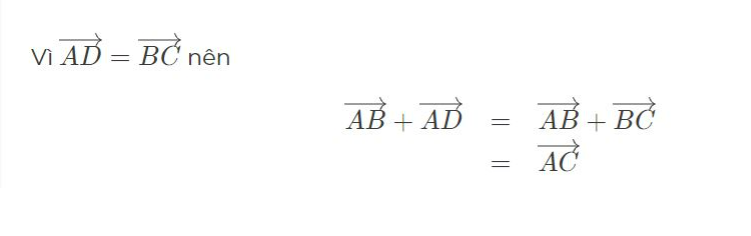
Trong vật lý, quy tắc này được dùng để biểu diễn hợp lực của hai lực quy đồng được biểu diễn bằng đường chéo của hình bình hành mà hai cạnh là những vecto biểu diễn hai lực thành phần. Phương pháp này giúp xác định được độ lớn và hướng của hợp lực một cách trực quan và dễ dàng.

Ngược lại. Cho tứ giác ABCD, nếu AB + AD = AC thì tứ giác ABCD là hình bình hành

Chứng minh:

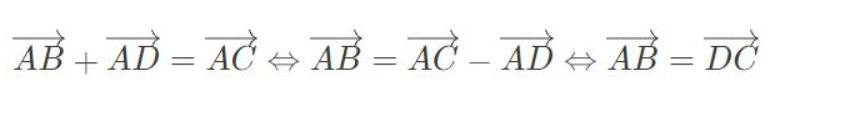
Đến đây chúng ta suy ra 2 vecto AB và DC có cùng hướng và độ dài bằng nhau. Khi đó tứ giác ABCD có một cặp cạnh đối song song và bằng nhau. Do đó tứ giác ABCD là hình bình hành.

Ví dụ: Cho hai lực F1 và F2 quy đồng tác dụng vào một vật, ta có thể vẽ một hình bình hành ABCD sao cho AB và AD là vecto biểu diễn F1 và F2. Khi đó, AC sẽ là vecto biểu diễn F – hợp lực của hai lực F1 và F2.

3. Công thức và ứng dụng:

3.1. Công thức tính chu vi hình bình hành:

– Công thức 1:

Công thức tính chu vi hình bình hành là:

Chu vi = 2 (a + b)

Trong đó, a và b là độ dài hai cạnh kề nhau của hình bình hành. Để tính được chu vi, ta cần biết độ dài hai cạnh kề nhau hoặc độ dài một cạnh và góc giữa hai cạnh kề nhau. Công thức này có thể được suy ra từ công thức tính chu vi hình chữ nhật, vì hình bình hành có thể được chuyển thành hình chữ nhật bằng cách cắt và dán một tam giác vuông.

Ví dụ: Cho 1 hình bình hành ABCD có 2 cạnh a và b lần lượt là 5 cm và 7 cm. Hỏi chu vi cảu hình bình hành là bao nhiêu?

Áp dụng công thức tính chu vi hình bình hành ta có:

C = (a +b) x 2 = (7 + 5) x 2 =12 x 2 = 24 cm

– Công thức 2:

Nếu biết góc giữa hai cạnh kề nhau, ta có thể sử dụng công thức:

a = c cos α

b = c sin α

Trong đó, c là độ dài đường chéo của hình bình hành, α là góc giữa đường chéo và một cạnh kề. Sau khi tính được a và b, ta thay vào công thức chu vi để tìm kết quả.

Ví dụ: Cho hình bình hành có độ dài đường chéo là 10 cm và góc giữa đường chéo và một cạnh kề là 60 độ. Tính chu vi của hình bình hành.

Ta có:

a = 10 cos 60 = 5 cm

b = 10 sin 60 = 8.66 cm

Chu vi = 2 (5 + 8.66) = 27.32 cm

3.2. Công thức tính diện tích hình bình hành:

Công thức 1:

Công thức tính diện tích hình bình hành là:

Diện tích = Chiều cao x Chiều dài cạnh đáy

Trong đó, chiều cao là khoảng cách từ một đỉnh của hình bình hành đến đường thẳng chứa cạnh đối của nó. Chiều dài cạnh đáy là độ dài của một cạnh bất kỳ của hình bình hành.

SABCD = a.h

Trong đó 

S là diện tích hình bình hành

a là cạnh đáy của hình bình hành

h là chiều cao, nối từ đỉnh tới đáy của một hình bình hành

– Công thức 2: Diện tích hình bình hành bằng tích của độ dài đường chéo và sin của góc giữa hai đường chéo. Công thức này có thể viết dưới dạng toán học như sau: S = d1.d2.sinα, trong đó S là diện tích, d1 và d2 là độ dài hai đường chéo, và α là góc giữa hai đường chéo.

– Công thức 3: Diện tích hình bình hành bằng nửa tích của độ dài hai cạnh kề nhau và sin của góc giữa hai cạnh đó. Công thức này có thể viết dưới dạng toán học như sau: S = (1/2).a.b.sinγ, trong đó S là diện tích, a và b là độ dài hai cạnh kề nhau, và γ là góc giữa hai cạnh đó.

Đây là một ví dụ về cách sử dụng các công thức trên để tính diện tích hình bình hành:

Cho một hình bình hành ABCD có AB = 8 cm, AD = 6 cm, AC = 10 cm, BD = 12 cm và góc A = 60°. Hãy tính diện tích của hình bình hành này.

Ta có thể áp dụng công thức 1 để tính diện tích. Đầu tiên, ta phải tìm chiều cao tương ứng với cạnh AB. Ta có thể vẽ một đường thẳng vuông góc với AB tại điểm E sao cho AE là chiều cao của hình bình hành. Ta có tam giác vuông AED có góc A = 60°, nên ta có thể sử dụng công thức lượng giác để tìm AE:

AE = AD.sinA = 6.sin60° = 6.(√3/2) = 3√3 cm

Do đó, diện tích của hình bình hành ABCD là:

S = AB.AE = 8.3√3 = 24√3 cm2

4. Bài tập vận dụng liên quan:

Bài 1: Cho hình bình hành có chu vi 364 cm và độ dài cạnh đáy gấp 6 lần cạnh kia, gấp 2 lần chiều cao. Hãy tính diện tích hình bình hành.

Hướng dẫn giải:

Nửa chu vi hình bình hành là: 364 : 2 = 182 (cm)

Cạnh đáy gấp 6 lần cạnh kia nên nửa chu vi sẽ gấp 7 lần cạnh kia.

Cạnh đáy hình bình hành là: 182 : 7 x 6 = 156 (cm)

Chiều cao hình bình hành là: 156 : 2 = 78 (cm)

Diện tích hình bình hành là: 156 x 78 = 12168 (cm2)

Bài 2: Cho hình bình hành có chu vi là 480 cm, có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành.

Hướng dẫn giải:

Ta có nửa chu vi hình bình hành là: 480 : 2 = 240 (cm)

Nếu như coi cạnh kia là 1 phần thì cạnh đáy chính là 5 phần như vậy.

Tính được chiều cao của hình bình hành là: 200 : 8 = 25 (cm)

Diện tích của hình bình hành là: 200 x 25 = 5000 (cm2)

Bài 3: Cho hình bình hành ABCD có chiều cao hạ xuống cạnh CD là 5, chiều dài cạnh CD là 15. Hãy tính diện tích hình bình hành ABCD. 

Hướng dẫn giải:

S (ABCD) = 5 x 15 = 75 cm2.

Bài 4: Mảnh đất hình bình hành có cạnh đáy là 47m, mở rộng đất bằng cách tăng các cạnh đáy của hình bình hành này thêm 7 m thì được mảnh đất hình bình hành mới có diện tích hơn diện tích mảnh đất ban đầu là 189m2. hãy tính diện tích mảnh đất ban đầu.

Hướng dẫn giải:

Phần diện tích tăng thêm chính là diện tích hình bình hành có cạnh đáy 7 m và chiều cao là chiều cao của mảnh đất hình bình hành ban đầu.

Hướng dẫn giải:

Chiều cao mảnh đất là: 189 : 7 = 27 (m)

Diện tích mảnh đất hình bình hành ban đầu là: 27 x 47 = 1269 (m2)