Phép cộng phân số (Giải bài tập Toán lớp 4 trang 126)

1. Phép cộng hai phân số:

a) Khi muốn thực hiện phép cộng hai phân số có cùng mẫu số, ta chỉ cần đơn giản là cộng hai tử số với nhau và giữ nguyên mẫu số. Điều này có nghĩa là chúng ta chỉ cần cộng các phần tử số trên số tử và giữ nguyên mẫu số. Ví dụ, nếu chúng ta muốn tính toán phép cộng giữa 2/3 và 1/3, chúng ta chỉ cần cộng 2 với 1 và giữ nguyên mẫu số 3. Kết quả cuối cùng sẽ là 3/3, tương đương với phân số đơn giản là 1.

b) Tuy nhiên, khi muốn cộng hai phân số có khác mẫu số, chúng ta cần thực hiện một bước quy đồng mẫu số. Điều này có nghĩa là chúng ta phải làm cho các mẫu số của hai phân số trở nên giống nhau trước khi thực hiện phép cộng. Để quy đồng mẫu số, chúng ta có thể nhân mẫu số của mỗi phân số với mẫu số của phân số còn lại. Sau đó, chúng ta chỉ cần cộng các phần tử số trên số tử và giữ nguyên mẫu số. Ví dụ, nếu chúng ta muốn tính toán phép cộng giữa 1/4 và 2/3, chúng ta cần quy đồng mẫu số của hai phân số này. Trong trường hợp này, chúng ta có thể nhân mẫu số của 1/4 với 3 và mẫu số của 2/3 với 4 để có mẫu số chung là 12. Tiếp theo, chúng ta cộng các phần tử số trên số tử, tức là 1 nhân với 3 và 2 nhân với 4, và giữ nguyên mẫu số 12. Kết quả cuối cùng sẽ là 7/12.

Chú ý: Trước khi thực hiện phép cộng hai phân số, chúng ta nên kiểm tra xem phân số thu được đã được tối giản hay chưa. Để tối giản phân số, chúng ta có thể chia tử số và mẫu số cho ước số chung lớn nhất của chúng. Nếu phân số chưa được tối giản, ta nên rút gọn phân số đó thành dạng tối giản để thuận tiện trong quá trình tính toán.

Cộng hai phân số là một phép toán quan trọng trong toán học và có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau như kinh tế, khoa học, và xã hội. Hiểu rõ cách thực hiện phép cộng hai phân số sẽ giúp chúng ta hiệu quả hơn trong việc giải quyết các bài toán liên quan đến phân số và phép cộng.

2. Tính chất của phép cộng phân số:

Phép cộng phân số là một khái niệm quan trọng trong toán học và có ứng dụng rộng rãi trong đời sống hàng ngày. Để hiểu rõ hơn về tính chất của phép cộng phân số, chúng ta có thể xem xét các điểm sau:

Tính chất giao hoán: Đây là tính chất cho biết việc thay đổi vị trí của các phân số trong một tổng không làm thay đổi kết quả của phép cộng. Nghĩa là ta có thể đổi chỗ các phân số trong tổng mà không ảnh hưởng đến kết quả cuối cùng.

Ví dụ: a + b = b + a

Tính chất kết hợp: Tính chất này cho phép chúng ta thực hiện phép cộng phân số theo bất kỳ thứ tự nào mà không làm thay đổi kết quả. Nghĩa là ta có thể cộng phân số thứ nhất với tổng của hai phân số còn lại hoặc cộng tổng hai phân số đó với phân số thứ ba mà không ảnh hưởng đến kết quả cuối cùng.

Ví dụ: (a + b) + c = a + (b + c)

Cộng với số 0: Đây là tính chất cho biết phân số nào cộng với số 0 đều bằng chính nó. Nghĩa là nếu ta cộng một phân số với số 0, kết quả sẽ không thay đổi.

Ví dụ: a + 0 = 0 + a = a

Bên cạnh những tính chất trên, phép cộng phân số còn được áp dụng trong nhiều bài toán thực tế. Ví dụ, khi chia đều một số lượng hàng hoặc tiền bằng nhau cho một nhóm người, chúng ta có thể sử dụng phép cộng phân số để tính toán và tìm ra kết quả chính xác.

Hy vọng rằng những thông tin trên đã giúp bạn hiểu rõ hơn về tính chất của phép cộng phân số và áp dụng nó trong các bài toán thực tế.

3. Các dạng toán:

Dạng 1: Tính tổng của hai phân số

Phương pháp: Để tính tổng của hai phân số, chúng ta áp dụng quy tắc cộng hai phân số lại với nhau. Đầu tiên, chúng ta tìm chung mẫu số chung của hai phân số, sau đó cộng tử số của hai phân số lại với nhau và giữ nguyên mẫu số. Cuối cùng, chúng ta rút gọn kết quả nếu cần thiết.

Dạng 2: Tính giá trị các biểu thức

Phương pháp: Khi tính giá trị các biểu thức, chúng ta áp dụng các quy tắc tính giá trị biểu thức. Đầu tiên, chúng ta ưu tiên tính toán trong ngoặc trước, sau đó thực hiện các phép tính nhân và chia trước, và phép cộng và trừ sau. Nếu có các phép tính có cùng mức ưu tiên, chúng ta thực hiện từ trái sang phải. Cuối cùng, chúng ta rút gọn kết quả nếu cần thiết.

Dạng 3: So sánh hai phân số

Phương pháp: Để so sánh các phân số, chúng ta tính giá trị của các biểu thức và sau đó áp dụng các quy tắc so sánh phân số. Đầu tiên, chúng ta tìm chung mẫu số chung của hai phân số, sau đó so sánh tử số của các phân số. Nếu tử số của phân số thứ nhất lớn hơn tử số của phân số thứ hai, ta kết luận rằng phân số thứ nhất lớn hơn phân số thứ hai. Ngược lại, nếu tử số của phân số thứ nhất nhỏ hơn tử số của phân số thứ hai, ta kết luận rằng phân số thứ nhất nhỏ hơn phân số thứ hai. Nếu tử số của hai phân số bằng nhau, chúng ta so sánh mẫu số của các phân số để đưa ra kết luận.

Dạng 4: Tìm x

Phương pháp: Để tìm giá trị của x trong biểu thức, chúng ta xác định xem x đóng vai trò nào trong biểu thức và sau đó áp dụng các quy tắc đã học lớp 3 để tìm giá trị của x. Nếu x xuất hiện ở dạng phân số, chúng ta tìm chung mẫu số chung của các phân số và giải phương trình để tìm giá trị của x.

Dạng 5: Tính nhanh phân số

Phương pháp: Để tính nhanh các phân số, chúng ta áp dụng các tính chất của phép cộng phân số và nhóm các phân số có thể tính toán dễ dàng. Nếu cùng có mẫu số chung, ta chỉ cần cộng tử số lại với nhau và giữ nguyên mẫu số. Nếu không có mẫu số chung, chúng ta tìm bội chung nhỏ nhất của các mẫu số và sau đó cộng tử số lại với nhau.

4. Giải bài tập Toán lớp 4 trang 126:

Khi ta đổi chỗ hai phân số trong một tổng thì tổng của chúng không thay đổi. Đây là một tính chất quan trọng trong toán học và có thể được giải thích một cách chi tiết như sau:

Trước tiên, hãy hiểu rõ về khái niệm phân số. Một phân số bao gồm hai thành phần: tử số và mẫu số. Tử số là phần trên của phân số và mẫu số là phần dưới của phân số. Ví dụ, trong phân số 1/2, số 1 là tử số và số 2 là mẫu số.

Khi ta đổi chỗ hai phân số trong một tổng, tức là hoán đổi vị trí của chúng, chúng ta thực sự không làm thay đổi giá trị tổng. Điều này có thể được minh chứng bằng cách tính giá trị của hai phân số ban đầu và so sánh kết quả với giá trị của hai phân số sau khi hoán đổi chỗ.

Để cộng hai phân số cùng mẫu số, chúng ta chỉ cần cộng hai tử số với nhau và giữ nguyên mẫu số. Ví dụ, để cộng 1/2 và 3/4, ta cộng tử số 1 và 3 để được tử số 4, và giữ nguyên mẫu số 4. Kết quả là 4/4, tương đương với phân số 1.

Điều này cho thấy rằng khi ta đổi chỗ hai phân số trong một tổng, tổng của chúng không thay đổi. Đây là một tính chất quan trọng trong toán học và có ứng dụng rộng rãi trong các bài toán liên quan đến phân số và tổng của chúng.

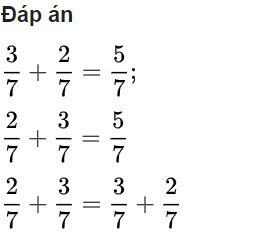
Khi chúng ta so sánh kết quả của hai phép tính, chúng ta có thể nhận thấy rằng khi chúng ta đổi chỗ hai phân số trong một tổng, tổng của chúng vẫn không thay đổi. Điều này đồng nghĩa với việc thứ tự của các phân số không ảnh hưởng đến kết quả cuối cùng. Điều này là một khái niệm quan trọng trong toán học và có thể được áp dụng trong nhiều bài toán khác nhau.

Giải Toán lớp 4 trang 126 Bài 3

Hai ô tô cùng chuyển gạo ở một kho. Ô tô thứ nhất chuyển được 2/7 số gạo trong kho, ô tô thứ hai chuyển được 3/7 số gạo trong kho.

Hỏi cả hai ô tô chuyển được bao nhiêu phần số gạo trong kho?

Phương pháp giải:

Số gạo cả hai ô tô chuyển được = số gạo ô tô thứ nhất chuyển được + số gạo ô tô thứ hai chuyển được.

Đáp án