Phân phối xác suất là một khái niệm trong lĩnh vực toán học, xác suất thống kê. Phân phối xác suất là phân phối tần suất lý thuyết biểu thị tần suất dự kiến để một biến cố cụ thể trung bình có thể xảy ra. Cùng bài viết này tìm hiểu cụ thể về phân phối xác suất nhé:
Mục lục bài viết
1. Khái niệm về phân phối xác suất (probability distribution):
Phân phối xác suất (probability distribution) là một khái niệm trong lý thuyết xác suất và thống kê, mô tả tần suất dự kiến của các giá trị, kết quả có thể xảy ra trong một biến cố cụ thể.
Một phân phối xác suất hay một hàm phân phối xác suất là một quy luật (dưới dạng hàm số) cho biết cách gán mỗi xác suất cho mỗi khoảng giá trị của tập số thực, cho biết xác suất của mỗi giá trị hoặc khoảng giá trị trong tập hợp các kết quả có thể xảy ra. Có nhiều loại phân phối xác suất khác nhau, mỗi loại đều có vai trò cung cấp thông tin về xác suất và khả năng xảy ra của các biến cố trong lý thuyết xác suất và thống kê, mỗi loại phân phối xác suất có các đặc điểm và ứng dụng riêng trong nhiều lĩnh vực khác nhau như kinh tế, khoa học dữ liệu, y học và nhiều lĩnh vực khác.
Lấy một ví dụ đăng trưng cơ bản thường thấy nhất về xác suất đó là: khi tung một đồng xu đồng nhất và cân đối, chúng ta có thể sử dụng phân phối xác suất để biểu thị khả năng xuất hiện mặt ngửa. Trong trường hợp này, phân phối xác suất cho khả năng xuất hiện mặt ngửa sẽ như sau:
– Số lần xuất hiện mặt ngửa: 0
=> Xác suất: 0.5
– Số lần xuất hiện mặt ngửa: 1
=> Xác suất: 0.5
Điều này có nghĩa là, phân phối xác suất cho khả năng xuất hiện mặt ngửa vfa mặt sấp khi tung đồng xu đồng nhất và cân đối, mỗi kết quả có khả năng xảy ra như nhau là 0.5.
2. Đặc trưng cơ bản của phân phối xác suất:
Phân phối xác suất là một khái niệm quan trọng trong lý thuyết xác suất và thống kê. Trong thực tế khi tìm xác suất ta thường chỉ xác định các đặc trưng cơ bản của phân phối xác suẩt rất khó xác định được hàm phân phối xác suất. Dưới đây là những đặc trưng cơ bản của phân phối xác suất:
– Miền giá trị hay khoảng biến thiên (Range): Miền giá trị của một phân phối xác suất là khoảng giá trị mà biến cố có thể xảy ra, là đại lượng đo mức độ trải dài của một tập dữ liệu nhất định từ nhỏ nhất (giới hạn dưới) đến lớn nhất (giới hạn trên), hoặc hiểu đươn giản miền giá trị (khoảng biến thiên) là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất trong một tập dữ liệu. Nó định nghĩa ranh giới của các kết quả có thể xảy ra và được xác định bởi các giới hạn dưới và giới hạn trên của biến cố.
– Hàm mật độ xác suất (Probability Density Function – PDF): Hàm mật độ xác suất được biểu diễn bằng một đồ thị liên tục (một đường biểu diễn) trong thống kê xác định tỷ lệ phân phối xác suất (khả năng xảy ra một kết quả) cho một biến ngẫu nhiên rời rạc hay các giá trị cụ thể trong miền giá trị của biến cố (ví dụ: cổ phiếu hoặc các quĩ ETF).
– Hàm phân phối xác suất (Cumulative Distribution Function – CDF): Hàm phân phối xác suất hay đơn giản là phân phối xác suất là một hàm gán các giá trị xác suất cho các giá trị mà biến ngẫu nhiên có thể nhận. Hàm phân phối xác suất được xác định cho các biến ngẫu nhiên rời rạc, nó tính tổng xác suất của tất cả các giá trị nhỏ hơn hoặc bằng một giá trị cụ thể trong miền giá trị của biến cố, không vượt qua một ngưỡng nhất định.
– Tham số (Parameters): Một phân phối xác suất có thể có các tham số để mô tả và định rõ đặc trưng của nó. Các tham số là phần hằng số hay giá trị không đổi trong một phương trình, có tác dụng cụ thể hóa mối quan hệ chính xác giữa các biến số. Các tham số này có thể bao gồm giá trị trung bình, phương sai, độ lệch chuẩn, và các tham số khác. Thông qua việc điều chỉnh các tham số này, ta có thể điều chỉnh hình dạng và đặc tính của phân phối xác suất.
– Kỳ vọng (Expectation): Kỳ vọng của biến ngẫu nhiên là trung bình của biến ngẫu nhiên. Xác suất kỳ vọng là giá trị trung bình dự kiến của một biến ngẫu nhiên được mô tả bởi phân phối xác suất. Nó đo lường trung bình của một biến cố và cho biết kỳ vọng giá trị nào có thể xảy ra trong thực tế.
Ý nghĩa của kỳ vọng:
Kỳ vọng toán phản ánh giá trị trung tâm của phân phối xác suất của biến ngẫu nhiên.
Trong kinh tế, kỳ vọng toán đồng thời mang 2 ý nghĩa:
+ Nếu xét trong 1 số lớn phép thử tương tự thì nó phản ánh giá trị trung bình
+ Nếu xét trong 1 phép thử đơn lẻ thì nó phản ánh giá trị mong đợi.
– Phương sai (variance): Dựa vào kì vọng ta sẽ có được trung bình của biến ngẫu nhiên, phương sai là một thước đo khoảng cách chênh lệch giữa các số liệu trong một tập dữ liệu với nhau so với giá trị trung bình của tập dữ liệu. Đây là một phương pháp sẽ cho ta thông tin về mức độ phân tán xác suất.
Ý nghĩa phương sai :
+ Phương sai phản ánh mức độ phân tán của các giá trị của biến ngẫu nhiên so với giá trị trung bình.
+ Phương sai càng lớn: phân tán càng nhiều quanh giá trị trung bình còn phương sai càng nhỏ: giá trị càng tập trung quanh giá trị trung bình.
+ Trong kinh tế, phương sai phản ánh mức độ rủi ro hay độ biến động (kém ổn định).
– Độ lệch chuẩn (Standard Deviation): Độ lệch chuẩn đo độ biến thiên của một biến cố trong phân phối xác suất. Nó cho biết mức độ phân tán của các giá trị quanh giá trị trung bình. Độ lệch chuẩn càng cao thì biến cố càng phân tán. Vì đơn vị của phương sai là bình phương nên việc tính để khớp với đơn vị của biến ngẫu nhiên là bất khả nên người ta đưa vào thêm khái niệm độ lệch chuẩn (SD-standard deviation) bằng căn bậc 2 của phương sai.
– Điểm chuẩn: Độ lệch chuẩn cho phép ta biết được mức độ phân tán trung bình của toàn bộ tập dữ liệu nhưng lại chưa cho ta biết được mức độ phân tán của 1 điểm nào đó. Chính vì vậy ta thêm một thông số nữa để đánh giá điểm này là điểm chuẩn (SC-Standard Score). Dựa vào điểm chuẩn ta có thể biết được rằng 1 điểm có nằm trong vùng phổ biến hay là không và nằm ở vị trí nào so với trung bình của toàn bộ tập mẫu. Điểm chuẩn còn được gọi là giá trị z (z-value), điểm z (z-score).
– Trung vị: Trung vị (median) là điểm chia đều xác suất thành 2 phần giống nhau, trung vị là nghiệm của phương trình hàm tích lũy xác suất:
– Moment (mô-men): Là khái niệm tổng quát của kì vọng và phương sai.
+ Kỳ vọng là moment bậc 1 với
+ Phương sai là moment bậc 2 với
Khi người ta thường gọi là moment quy tâm, còn gọi là moment gốc. Vậy nên ta có thể gọi kỳ vọng là moment gốc bậc 1 và phương sai là moment quy tâm bậc 2.
3. Các loại phân phối xác suất:
Dưới đây là một số loại phân phối xác suất phổ biến:
– Phân phối chuẩn (Normal distribution): Còn được gọi là phân phối Gauss hoặc phân phối hình chuông. Đây là phân phối đối xứng và được xác định bởi hai tham số là giá trị trung bình và độ lệch chuẩn. Phân phối chuẩn có hình dạng hình chuông đối xứng và được sử dụng rộng rãi trong thống kê vì nhiều biến ngẫu nhiên trong tự nhiên được xấp xỉ bằng phân phối chuẩn khi kích thước mẫu lớn.
– Phân phối Poisson: Được sử dụng để mô hình hóa số lần xảy ra của một sự kiện trong một khoảng thời gian cố định. Phân phối Poisson không âm và không có giới hạn trên. Nó thường được sử dụng trong các ứng dụng đếm như mô hình lưu lượng cuộc gọi điện thoại, số lượng sự cố xảy ra trong một khoảng thời gian nhất định, hay số lượng sản phẩm được sản xuất trong một dây chuyền sản xuất.
– Phân phối đều hay phân phối đồng nhất (Uniform distribution): Đây là một dạng phân phối xác suất trong đó mỗi giá trị trong khoảng xác định có đều có khả năng xảy ra như nhau, mỗi biến có cùng một xác suất để cho ra một kết quả. Phân phối đều được sử dụng để mô hình hóa các biến ngẫu nhiên mà không có sự chênh lệch đáng kể giữa các giá trị trong khoảng.
– Phân phối đa thức (Multinomial distribution): Đây là loại phân phối xác suất được sử dụng trong tài chính, dùng để mô hình hóa việc xảy ra của nhiều sự kiện đồng thời, trong đó mỗi sự kiện có một số khả năng xảy ra cụ thể, để từ đó xác định tình hình thu nhập của công ty. Phân phối đa thức thường được sử dụng trong các bài toán phân loại và phân phối xác suất của dữ liệu rời rạc. Ngoài ra, phân phối nhị thức được biết đến rộng rãi hơn là một loại phân phối đa thức đặc biệt trong đó chỉ có hai kết quả có thể xảy ra, chẳng hạn như đúng / sai hoặc đầu / đuôi.
– Phân phối t (Student’s t-distribution): Được sử dụng trong các bài toán khi kích thước mẫu nhỏ và không biết độ lệch chuẩn của quần thể. Phân phối t có hình dạng giống phân phối chuẩn nhưng có đuôi dày hơn.
– Phân phối F (F-distribution hay phân phối Fisher Snedecor): Được sử dụng trong kiểm định thống kê, diễn tả phân phối xác suất liên lục với tần suất xuất hiện tương tự như phân phối rỗng của thống kê kiểm thử, đặc biệt là khi so sánh phương sai hoặc kiểm thử F. Phân phối F là một phân phối dương và không đối xứng.
Ngoài ra, còn nhiều loại phân phối khác như phân phối gamma, phân phối exponential, phân phối binomial, phân phối chi bình phương,… Mỗi loại phân phối có các đặc điểm riêng và được sử dụng trong các bài toán thống kê và xác suất cụ thể.
4. Phân phối xác suất có vai trò như thế nào?
Phân phối xác suất là một khái niệm có vai trò quan trọng trong lý thuyết xác suất và thống kê ứng dụng. Một số vai trò chính của phân phối xác suất đó là:
– Mô hình hóa dữ liệu và dự đoán: Phân phối xác suất giúp ta mô hình hóa dữ liệu và mô tả sự biến thiên của các biến ngẫu nhiên và dữ liệu thực tế, xây dựng các mô hình thống kê và dự đoán. Bằng cách chọn một phân phối phù hợp, ước lượng các tham số của nó từ dữ liệu, ta có thể lấy giá trị xấp xỉ của dữ liệu và hiểu được phân phối của chúng. Điều này cho phép ta tính toán xác suất xảy ra của các sự kiện cụ thể, giúp ta rút ra những phân tích, suy luận và dự đoán hợp lý từ dữ liệu, xây dựng mô hình để dự đoán kết quả tương lai hoặc hiểu sự tương quan giữa các biến.
– Xác định xác suất: Phân phối xác suất cho phép ta tính toán xác suất xảy ra của các sự kiện. Bằng cách sử dụng phân phối xác suất, ta có thể đưa ra dự đoán về xác suất xảy ra của một biến ngẫu nhiên cụ thể trong một phạm vi hoặc một điều kiện cho trước.
– Kiểm định thống kê: Phân phối xác suất cung cấp cơ sở để thực hiện các kiểm định thống kê. Các kiểm định thống kê sử dụng phân phối xác suất để đánh giá tính đáng tin cậy của kết quả và rút ra các kết luận về một giả thuyết được đưa ra.
5. Một số ví dụ về phân phối xác suất:
Bài 1: Cho biến ngẫu nhiên rời rạc X với bảng phân phối xấc suất được cho như sau:
| X | -2 | -1 | 0 | 1 | 2 |
| P(X) | 1/8 | 2/8 | 2/8 | 2/8 | 1/8 |
a) P(X ≤ 2); P(X>-2); P(-1≤ X≤1);P(X ≤ -1 hoặc X=2)
b) Xác định hàm phân phối tích lũy và tinh các xác suất sau: P(X≤1.25);P(X≤2.2)
c) Tính kỳ vọng và phương sai của X
Giải
a. P(X)=1/8+2/8+2/8+2/8+1/8=1
P(X>-2)=2/8+2/8+2/8+1/8=7/8
P(-1≤ X≤1)=2/8+2/8+2/8=6/8
P(X ≤ -1 hoặc X=2)=1/8+2/8+1/8=1/2
b.Hàm phân phối tích luỹ:
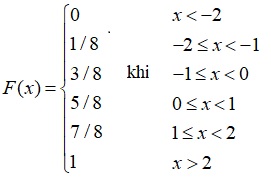
Vậy P(X≤1.25)=7/8; P(X≤2.2)=1
c. – Kỳ vọng và phương sai của X
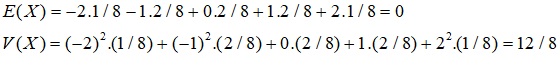
Bài 2: Một nhân viên kỹ thuật của một công ty đã đưa ra một sản phẩm mới. Công ty ước tính nếu đưa sản phẩm ra thị trường thì xác suất rất thành công là 0.6, xác suất thành công là 0.3 và xác suất không thành công là 0.1. Thu nhập tương ứng cho các trường hợp này là 15 triệu đô la, 5 triệu đô la và – 500 000 đô la. Gọi X là biến ngẫu nhiên thu nhập nhận được.
a) Lập bản phân phối xác suất của biến ngẫu nhiên
b) Xác định hàm phân phối tích lũy của X.
c) Xác định kỳ vọng phương sai và độ lệch chuẩn của X.
Giải
a. Hàm xác suất thu nhập nhận được là:
| X | -500 000 | 5 triệu | 15 triệu |
| P | 0.1 | 0.3 | 0.6 |
b. Hàm phân phối tích luỹ

c. Kỳ vọng
E(X)=-500000.0.1+5000000.0.3
+15000000.0.6=10450000
V(X)=[(-500000)^2.0.1+(5000000)^2.0.3+(15000000)^2.0.6]-(10450000)^2=3.33×10^13
Độ lệch chuẩn của X là sqrt(3.33×10^13)




