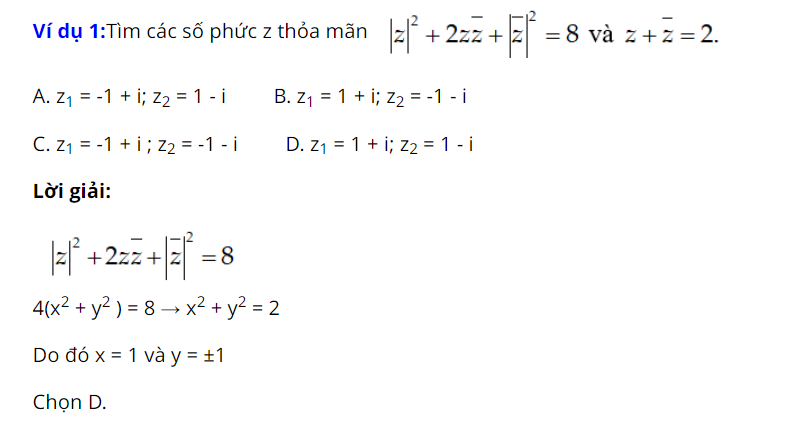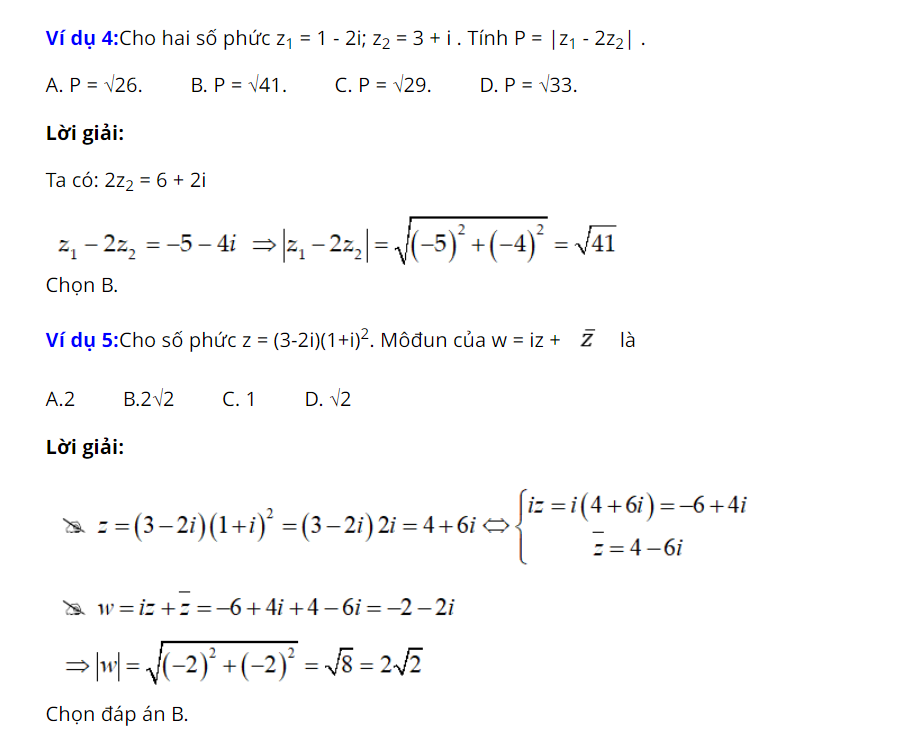Mô đun số phức là một chủ đề quan trọng trong toán học. Để hiểu và áp dụng phương pháp giải số phức, chúng ta cần nắm vững các khái niệm và quy tắc liên quan. Bên cạnh đó, việc làm bài tập có đáp án cũng rất quan trọng để rèn kỹ năng và củng cố kiến thức. Mời bạn đọc tham khảo.
Mục lục bài viết
1. Modun của số phức là gì?
Modun (Tiếng Anh: modulus hoặc absolute) của số phức z=a+bi (a, b ∈ R) là căn bậc hai số học (hay căn bậc hai không âm) của a²+b². Chẳng hạn như 3+4i có 3²+4²=25 nên modun của 3+4i bằng 5. Ta cũng ký hiệu modun của z=a+bi là |z| hoặc |a+bi|. Với lưu ý số thực cũng là một số phức. Ta cũng dễ nhận thấy rằng trị tuyệt đối của một số thực cũng chính là modun của số thực đó. Do đó đôi khi ta cũng gọi mô đun của số phức là giá trị tuyệt đối cúa số phức.
Modun của một số phức được sử dụng để đo độ dài của số phức đó từ gốc tọa độ (0, 0) trong mặt phẳng phức. Nó tương đương với khoảng cách từ điểm biểu diễn của số phức đến gốc tọa độ. Ví dụ, nếu chúng ta có số phức z = 3 + 4i, thì modun của z là căn bậc hai của 3^2 + 4^2 = 25, hay là 5. Điều này có nghĩa là số phức z cách gốc tọa độ 5 đơn vị.
Modun cũng có thể được hiểu như giá trị tuyệt đối của số phức. Điều này có nghĩa là nếu ta có số phức z = a + bi, thì modun của z, ký hiệu là |z|, sẽ bằng căn bậc hai của a^2 + b^2. Chẳng hạn, nếu ta có số phức z = -2 – 3i, thì modun của z sẽ là căn bậc hai của (-2)^2 + (-3)^2 = 13, hay là căn bậc hai của 13, xấp xỉ là 3.605. Điều này cho biết rằng số phức z cách gốc tọa độ khoảng 3.605 đơn vị.
Vì vậy, modun của một số phức không chỉ cho chúng ta biết về độ dài của số phức đó, mà còn cho chúng ta biết về khoảng cách từ số phức đó đến gốc tọa độ và cũng tương đương với giá trị tuyệt đối của số phức đó.
Trong toán học, modun của số phức cũng có rất nhiều ứng dụng trong các lĩnh vực khác nhau. Trong đại số tuyến tính, modun được sử dụng để xác định các không gian vector và tính toán khoảng cách giữa các vector. Trong phương trình vi phân, modun được sử dụng để định nghĩa các dạng số phức và tính toán phép tích phân phức. Trong hình học, modun được sử dụng để đo độ dài các đoạn thẳng và tính toán diện tích và thể tích của các hình học phức tạp. Ngoài ra, modun còn có ứng dụng trong các lĩnh vực kỹ thuật và khoa học tự nhiên như điện tử, vật lý lượng tử, và xử lý tín hiệu.
Hiểu rõ về modun của số phức là một yếu tố quan trọng giúp chúng ta áp dụng các khái niệm và công thức toán học vào thực tế và nghiên cứu. Nó không chỉ giúp chúng ta hiểu và mô hình hóa các hiện tượng trong thế giới thực mà còn cung cấp một công cụ mạnh mẽ để giải quyết các bài toán phức tạp trong nhiều lĩnh vực khác nhau.
![]()
Ví dụ:
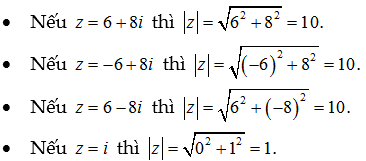
Về mặt hình học, mỗi số phức z=a+bi (a,b∈R) được biểu diễn bởi một điểm M(z)=(a;b) trên mặt phẳng Oxy và ngược lại. Điều này có nghĩa là chúng ta có thể tìm một điểm trên mặt phẳng Oxy tương ứng với mỗi số phức z. Khi đó, modun của z có thể được biểu diễn bằng độ dài đoạn thẳng OM(z). Điều này có nghĩa là chúng ta có thể đo độ dài đoạn thẳng OM để tìm giá trị modun của số phức z.
Modun của số phức z thường được ký hiệu là |z|. Đây là một số thực không âm, có thể hiểu là khoảng cách từ điểm M(z) đến gốc tọa độ O. Khi đó, nếu |z| bằng 0, tức là khoảng cách từ điểm M(z) đến gốc tọa độ O bằng 0, thì số phức z sẽ bằng 0. Điều này cũng có thể hiểu là số phức z không có phần thực và phần ảo, tức là z=0.
Ngoài ra, khi chúng ta biểu diễn số phức z dưới dạng z=a+bi, ta cũng có thể biểu diễn nó dưới dạng z=r(cosθ + isinθ), trong đó r là modun của z và θ là góc mà đoạn thẳng OM tạo với trục thực dương. Điều này giúp chúng ta có thể mô tả số phức z bằng cách sử dụng modun và góc của nó, mở rộng khái niệm về số phức và tạo ra nhiều biểu diễn khác nhau cho cùng một số phức.
Vì vậy, modun của số phức z mang thông tin về khoảng cách từ điểm M(z) đến gốc tọa độ O. Nếu modun của z lớn, tức là khoảng cách lớn, và nếu modun của z nhỏ, tức là khoảng cách nhỏ. Điều này giúp chúng ta hiểu về tính chất và vị trí của số phức trên mặt phẳng Oxy.
Ngoài ra, modun của số phức z còn có thể biểu thị cho độ lớn của số phức đó. Nếu modun của z lớn, tức là độ lớn của số phức lớn và nếu modun của z nhỏ, tức là độ lớn của số phức nhỏ. Điều này cho chúng ta biết được số phức z có giá trị lớn hay nhỏ hơn trong quá trình tính toán và phân tích các bài toán liên quan đến số phức.
Do đó, modun của số phức z là một khái niệm quan trọng trong toán học và có nhiều ứng dụng trong các lĩnh vực khác nhau như đại số, hình học, vật lý và kỹ thuật.
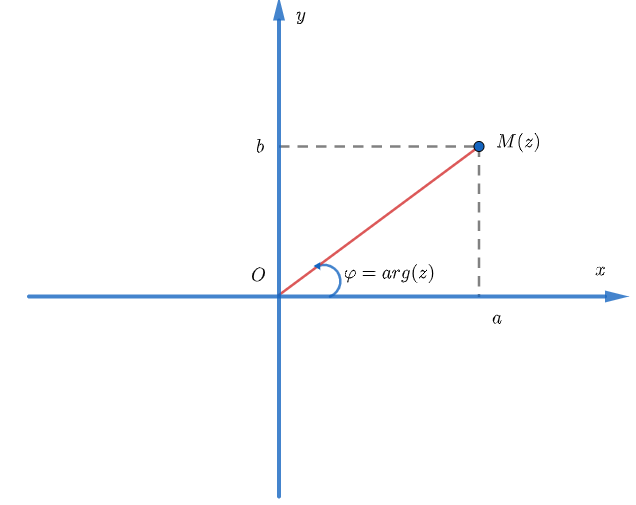
Tính chất mô đun của số phức là một khái niệm quan trọng trong toán học và có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Mô đun của một số phức được định nghĩa là khoảng cách từ gốc tọa độ đến điểm biểu diễn số phức đó trong mặt phẳng phức. Trong bài viết này, chúng ta sẽ tìm hiểu về các tính chất của mô đun số phức.
(i) Một tính chất đơn giản của mô đun số phức là hai số phức đối nhau có cùng mô đun. Điều này có nghĩa là nếu ta có số phức z, thì mô đun của số phức đối của z (ký hiệu là -z) sẽ bằng mô đun của z. Toán tử đối trong số phức thực hiện việc đảo ngược phần thực và phần ảo của số phức.
(ii) Mô đun của một số phức liên hợp cũng bằng mô đun của số phức ban đầu. Số phức liên hợp của số phức a+bi được ký hiệu là a-bi, và mô đun của số phức này sẽ bằng mô đun của số phức gốc. Điều này có nghĩa là tính chất mô đun không bị ảnh hưởng bởi phần ảo của số phức.
(iii) Mô đun của số phức bằng 0 khi và chỉ khi số phức đó là số 0. Điều này có nghĩa là nếu ta có số phức z và mô đun của z bằng 0, thì z sẽ là số 0, tức là không có phần thực và phần ảo.
(iv) Một tính chất quan trọng khác của mô đun số phức là tích của hai số phức liên hợp bằng bình phương của mô đun của chúng. Điều này có nghĩa là nếu ta có hai số phức a+bi và c+di, thì mô đun của tích hai số này sẽ bằng bình phương của mô đun của số phức a+bi nhân mô đun của số phức c+di. Tức là |(a+bi)(c+di)| = |a+bi|^2 * |c+di|^2.
(v) Mô đun của một tích bằng tích của các mô đun tương ứng. Điều này có nghĩa là nếu ta có n số phức z1, z2, …, zn, thì mô đun của tích của các số này sẽ bằng tích của các mô đun tương ứng. Tức là |z1 * z2 * … * zn| = |z1| * |z2| * … * |zn|.
(vi) Mô đun của một thương bằng thương của các mô đun. Điều này có nghĩa là nếu ta có hai số phức a+bi và c+di, với c+di khác 0, thì mô đun của thương hai số này sẽ bằng thương của mô đun của số phức a+bi chia cho mô đun của số phức c+di. Tức là |(a+bi)/(c+di)| = |a+bi| / |c+di|.
Trên đây là một số tính chất cơ bản của mô đun số phức. Chúng có vai trò quan trọng trong việc phân tích và thực hiện các phép toán trên số phức. Hiểu rõ về tính chất mô đun sẽ giúp chúng ta áp dụng chúng một cách hiệu quả trong các bài toán và ứng dụng thực tế.
2. Phương pháp giải:

3. Bài tập có đáp án: