Lý thuyết và bài tập về Giản đồ Frenen dòng điện xoay chiều

22/09/202422/09/2024

22/09/2024

Hiện nay, việc ứng dụng phương pháp giản đồ Frenen để giải các bài toán liên quan đến dao động điều hòa, sóng cơ và điện xoay chiều là khá phổ biến, cùng bài viết này tìm hiểu lý thuyết và một số bài tập vận dụng nhé:

Mục lục bài viết

1 1. Khái niệm về dòng điện xoay chiều:

2 2. Phương pháp giản đồ Fre-nen:

3 3. Bài tập về dòng điện xoay chiều:

3.1 3.1. Dạng 1 – Xác định suất điện động cảm ứng:
3.2 3.2. Dạng 2 – Điện lượng qua tiết diện dây dẫn:
3.3 3.3. Dạng 3 – Bài tập sử dụng phương pháp giản đồ vecto:

1. Khái niệm về dòng điện xoay chiều:

– Dòng điện xoay chiều là dòng điện có cường độ biến thiên tuần hoàn với thời gian theo quy luật của hàm số sin hay cosin, với dạng tổng quát: $i=Iocos(ωt+φi)”> i = I_{o.} c o s (ω t + φ_{i})$

+ i: giá trị của cường độ dòng điện tại thời điểm t, được gọi là giá trị tức thời của i (cường độ tức thời).

+ I₀ > 0: giá trị cực đại của i (cường độ cực đại). * ω > 0: tần số góc.

+ f: tần số của i. T: chu kì của i.

+ (ωt + φ): pha của i.

+ φ_i là pha ban đầu của dòng điện

2. Phương pháp giản đồ Fre-nen:

– Yêu cầu bài toán: tìm li độ của một vật thực hiện đồng thời 2 dao động điều hòa cùng phương, cùng tần số:

x₁ = A₁cos⁡(ωt + φ₁ )

x₂ = A₂cos⁡(ωt + φ₂ )

Khi đó li độ của vật x = x₁ + x₂ có phương trình như thế nào?

– Phương pháp giản đồ Fre-nen.

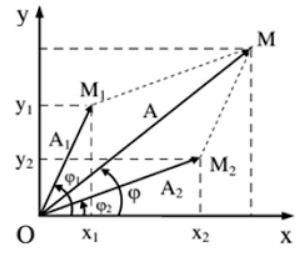
Bước 1: biểu diễn li độ x₁, x₂ tại thời điểm ban đầu bằng các Vectơ OM₁, vecto OM₂

Bước 2: li độ x = x₁ + x₂ của dao động tổng hợp tại thời điểm ban đầu được biểu diễn bằng vecto OM = vecto OM₁ + vecto OM₂

Bước 3: Sử dụng quy tắc hình bình hành để tìm các đại lượng đặc trưng.

+ Phương dao động: cùng phương với 2 dao động thành phần.

+ Tần số: cùng tần số ω với 2 dao động thành phần.

+ Biên độ:

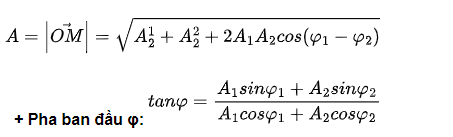
– Nhận xét: biên độ A phụ thuộc vào A₁, A₂ và độ lệch pha (φ₁ – φ₂)

+) A_max = A₁ + A₂ khi 2 dao động cùng pha: (φ₁ – φ₂ ) = 2nπ (n = 0, ±1, ±2,…)

+) A_min = |A₁ – A₂ | khi 2 dao động ngược pha: (φ₁ – φ₂ ) = (2n + 1)π (n = 0, ±1, ±2,…)

3. Bài tập về dòng điện xoay chiều:

3.1. Dạng 1 – Xác định suất điện động cảm ứng:

Bài 1 : Một khung dây dẫn phẳng có diện tích S = 50 cm², có N = 100 vòng dây, quay đều với tốc độ 50 vòng/giây quanh một trục vuông góc với các đường sức của một từ trường đều có cảm ứng từ B = 0,1 T. Chọn gốc thời gian t = 0 là lúc vectơ pháp tuyến $n\to”> ⃗ n$ của diện tích S của khung dây cùng chiều với vectơ cảm ứng từ B và chiều dương là chiều quay của khung dây.

a) Viết biểu thức xác định từ thông Φ qua khung dây.

b) Viết biểu thức xác định suất điện động e xuất hiện trong khung dây.

c) Vẽ đồ thị biểu diễn sự biến đổi của e theo thời gian.

Hướng dẫn giải:

a) Khung dây dẫn quay đều với tốc độ góc : ω = 50.2π = 100π rad/s

Tại thời điểm ban đầu t = 0, vectơ pháp tuyến $n ⃗ n$ của diện tích S của khung dây có chiều trùng với chiều của vectơ cảm ứng từ B của từ trường. Đến thời điểm t, pháp tuyến $n$ của khung dây đã quay được một góc bằng ωt . Lúc này từ thông qua khung dây là :

$Φ=NBS”> Φ = N B S$ cos(ωt )

Như vậy, từ thông qua khung dây biến thiên điều hoà theo thời gian với tần số góc ω và với giá trị cực đại (biên độ) là Ф₀= NBS.

Thay N = 100, B = 0,1 T, S = 50 cm² = 50. 10^-4 m² và ω = 100π rad/s ta được biểu thức của từ thông qua khung dây là :

$Φ=0,05cos(100πt)”> Φ = 0, 05 c o s (100 π t)$ (Wb)

b) Từ thông qua khung dây biến thiên điều hoà theo thời gian, theo định luật cảm ứng điện từ của Faraday thì trong khung dây xuất hiện một suất điện động cảm ứng.

Suất điện động cảm ứng xuất hiện trong khung dây được xác định theo định luật Lentz :

$e=-dΦdt=-Φt'=ωNBSsin(ωt)=ωNBScos(ωt-π2)”> e = - \frac{d Φ}{d t} = - Φ_{t}^{'} = ω N B S s i n (ω t) = ω N B S c o s (ω t - \frac{π}{2})$

Như vậy, suất điện động cảm ứng xuất hiện trong khung dây biến đổi điều hoà theo thời gian với tần số góc ω và với giá trị cực đại (biên độ) là E₀ = ωNBS.

Thay N = 100, B = 0,1 T, S = 50 cm² = 50. 10^-4 m² và ω = 100π rad/s ta được biểu thức xác định suất điện động xuất hiện trong khung dây là :

$e=5πcos(100πt-π2)”> e = 5 π c o s (100 π t - \frac{π}{2)}$ (V) hay $e\approx15,7cos(314t-π2)”> e \approx 15, 7 c o s (314 t - \frac{π}{2})$ (V)

c) Suất điện động xuất hiện trong khung dây biến đổi điều hoà theo thời gian với chu khì T và tần số f lần lượt là:

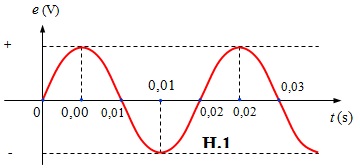
$T=2πω=2π100π=0,02s;f=1T=10,02=50Hz”> T = \frac{2 π}{ω} = \frac{2 π}{100 π} = 0, 02 s; f = \frac{1}{T} = \frac{1}{0, 02} = 50 H z$

Đồ thị biểu diễn sự biến đổi của suất điện động e theo thời gian t là đường hình sin có chu kì tuần hoàn T = 0,02 s.Bảng giá trị của suất điện động e tại một số thời điểm đặc biệt như : 0 s, $T/4 = 0,005 s; T/2 = 0,01 s, 3T/4 = 0,015 s, T = 0,02s, 5T/4 = 0,025s$ và $3T/2=0,03 s$ :

t (s)	0	0,005	0,01	0,015	0,02	0,025	0,03
e (V)	0	15,7	0	-15,7	0	15,7	0

Đồ thị biểu diễn sự phụ thuộc của e theo t như hình trên H1 :

3.2. Dạng 2 – Điện lượng qua tiết diện dây dẫn:

Bài 1: Dòng điện xoay chiều i=2sin100πt(A) qua một dây dẫn . Điện lượng chạy qua tiết diện dây trong khoảng thời gian từ 0 đến 0,15s là :

A.0 B.4/100π(C) C.3/100π(C) D.6/100π(C)

Hướng dẫn giải:

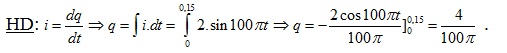
Đáp án: B

Bài 2: Dòng điện xoay chiều có biểu thức $i=2cos100πt(A)$ chạy qua dây dẫn. Điện lượng chạy qua một tiết điện dây trong khoảng thời gian từ 0 đến 0,15s là :

A. 0 B. $4/100π (C)$ C. $3/100π (C)$ D. $6/100π (C)$

$Hướng dẫn giải:$

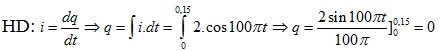
Đáp án: A

3.3. Dạng 3 – Bài tập sử dụng phương pháp giản đồ vecto:

Bài 1. Đặt một hiệu điện thế u = U√2cos(ωt) vào hai đầu đoạn mạch RLC mắc nối tiếp, trong đó cuộn dây thuần cảm, hiệu điện thế hiệu dụng U_RL = √13U_C và hiệu điện thế U_C lệch pha 2π/3 so với U. Tỉ số U/U_C ?

A. (√5)/2 . B. 3. C. 2. D. 2/5 .

Lời giải:

Chọn D.

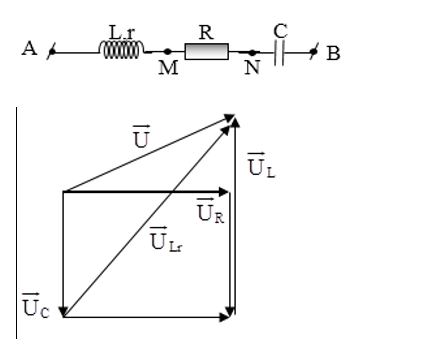
Theo giản đồ vecto ta có: U²_RL = U² = U_C² – 2UU_Ccos120° (1)

Mặt khác theo bài ra : U_RL = U_C√13 (2)

Từ (1) và (2) ta có:

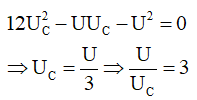
Bài 2. Đặt một điện áp xoay chiều vào hai đầu đoạn mạch L, R, C mắc nối tiếp theo thứ tự đó. Điện áp hai đầu đoạn các đoạn mạch chứa L, R có biểu thức: u_LR = 150cos(100πt + π/3) (V). Cho R = 25Ω. Cường độ dòng điện trong mạch có giá trị hiệu dụng bằng:

A. 3A. B. 3√2 A. C. (3√2)/2 A. D. 3,3 A.

Lời giải:

Chọn C.

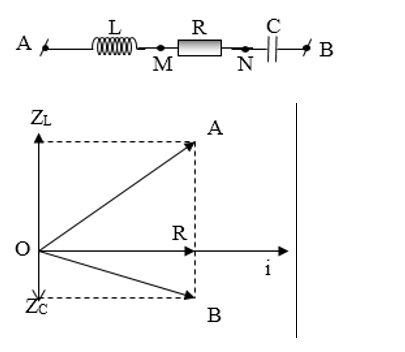
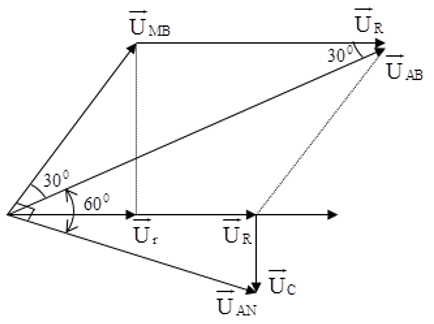
Bài 3. Cho mạch điện AB gồm một điện trở thuần R mắc nối tiếp với một tụ điện C và một cuộn dây theo đúng thứ tự. Gọi M là điểm nối giữa điện trở thuần và tụ điện, N điểm nối giữa tụ điện và cuộn dây. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có giá trị hiệu dụng 120√3 V không đổi, tần số f = 50Hz thì đo đươc điện áp hiệu dụng giữa hai điểm M và B là 120V, điện áp U_AN lệch pha π/2 so với điện áp U_MB đồng thời U_AB lệch pha π/3 so với U_AN. Biết công suất tiêu thụ của mạch khi đó là 360W. Nếu nối tắt hai đầu cuộn dây thì công suất tiêu thụ của mạch là :

A. 810W B. 240W C. 540W D. 180W

Lời giải:

Chọn C.

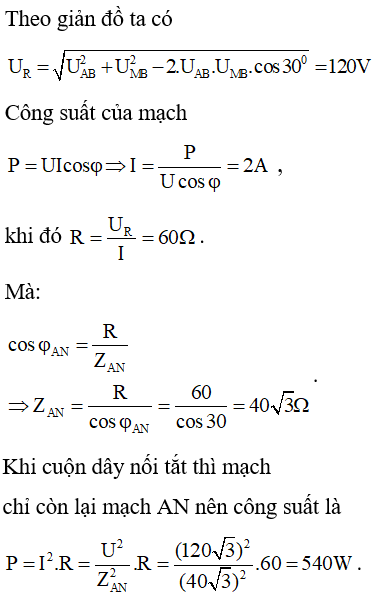
Bài 4. Đặt điện áp u = U₀cosωt (U₀ và ω không đổi) vào hai đầu đoạn mạch AB theo thứ tự gồm một tụ điện, một cuộn cảm thuần và một điện trở thuần mắc nối tiếp. Gọi M là điểm nối giữa tụ điện và cuộn cảm. Biết điện áp hiệu dụng giữa hai đầu AM bằng điện áp hiệu dụng giữa hai đầu MB và cường độ dòng điện trong đoạn mạch lệch pha π/12 so với điện áp giữa hai đầu đoạn mạch. Hệ số công suất của đoạn mạch MB.

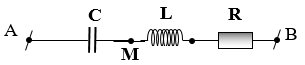
A. (√3)/2 B. 0,26 C. 0,50 D. (√2)/2

Lời giải:

Chọn C.

Cách giải 1:

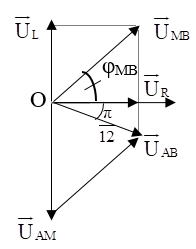
Vẽ giản đồ véctơ.

Xét tứ giác hình thoi:

φ_MB = π/3 ⇒ cosφ_MB = 1/2

Cách giải 2:

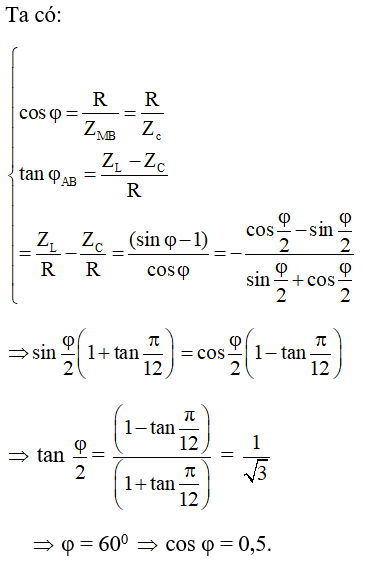
Bài 5. Cho đoạn mạch AB gồm hai đoạn mạch AM nối tiếp với MB. Biết đoạn AM gồm R nối tiếp với C và MB có cuộn cảm có độ tự cảm L và điện trở r. Đặt vào AB một điện áp xoay chiều u = U√2cosωt (V). Biết R = r = √(L/C), điện áp hiệu dụng giữa hai đầu MB lớn gấp n = √3 điện áp hai đầu AM. Hệ số công suất của đoạn mạch có giá trị là

A. 0,866 B. 0,975 C. 0,755 D. 0,887

Lời giải:

Chọn A.

Vẽ giản đồ véctơ như hình vẽ.

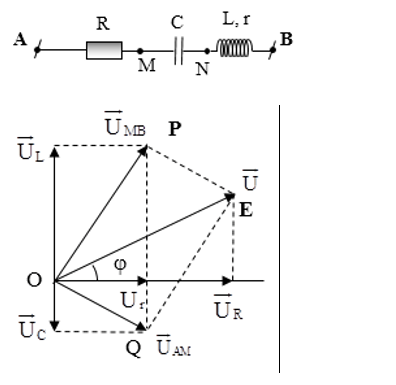
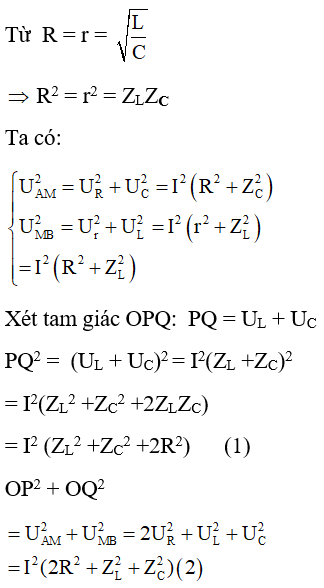
Từ (1) và (2) ta thấy PQ² = OP² + OQ² ⇒ tam giác OPQ vuông tại O.

Từ U_MB = nU_AM = U_AM√3 ta có:

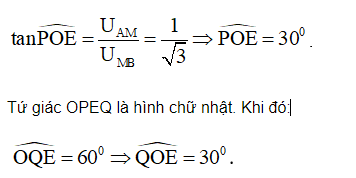
Do đó góc lệch pha giữa u và i trong mạch: φ = 90° – 60° = 30°.

Vì vậy cosφ = cos30° = (√3)/2 = 0,866 .

Bài 7. Trên đoạn mạch xoay chiều không phân nhánh có bốn điểm theo đúng thứ tự A, M, N và B. Giữa hai điểm A và M chỉ có cuộn cảm thuần, giữa hai điểm M và N chỉ có điện trở thuần, giữa 2 điểm N và B chỉ có tụ điện. Điện áp hiệu dụng giữa hai điểm A và M là 150 (V) và điện áp hiệu dụng giữa hai điểm N và B là 200/3 (V). Điện áp tức thời trên đoạn AN và trên đoạn MB lệch pha nhau 90°. Điện áp hiệu dụng trên R là

A. 100 (V). B. 120 (V).

C. 90 (V). D. 180 (V).

Lời giải:

Chọn A

Bài 8. Mạch điện xoay chiều nối tiếp AB theo đúng thứ tự gồm cuộn cảm thuần L, điện trở thuần R và tụ điện C. Cho biết điện áp hiệu dụng U_RC = 0,75U_RL và R² = L/C. Tính hệ số công suất của đoạn mạch AB.

A. 0,8. B. 0,864. C. 0,5. D. 0,867.

Lời giải:

Chọn B

Bài 9. Mạch điện xoay chiều nối tiếp AB theo đúng thứ tự gồm cuộn cảm thuần L, điện trở thuần R và tụ điện C. Cho biết điện áp hiệu dụng U_RL = U_RC√3 và R² = L/C. Tính hệ số công suất của đoạn mạch AB.

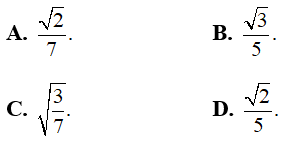
Lời giải:

Chọn C

Bài 10. Trên đoạn mạch xoay chiều không phân nhánh có bốn điểm theo đúng thứ tự A, B, C và D. Giữa hai điểm A và B chỉ có tụ điện, giữa hai điểm B và C chỉ có điện trở thuần, giữa 2 điểm C và D chỉ có cuộn cảm thuần cảm. Điện áp hiệu dụng giữa hai điểm A và D là 100√3 (V) và cường độ hiệu dụng chạy qua mạch là 1 (A). Điện áp tức thời trên đoạn AC và trên đoạn BD lệch pha nhau 60° nhưng giá trị hiệu dụng thì bằng nhau. Dung kháng của tụ điện là

A. 40 Ω B. 100 Ω C. 50√3 Ω D. 20 Ω

Lời giải:

Chọn B