Khi góc tới tăng 2 lần thì góc khúc xạ tăng bao nhiêu lần?

1. Khi góc tới tăng 2 lần thì góc khúc xạ tăng bao nhiêu lần?

Góc tới và góc khúc xạ là hai đại lượng có liên quan đến hiện tượng khúc xạ ánh sáng khi ánh sáng đi qua các môi trường khác nhau. Góc tới là góc giữa tia tới và pháp tuyến của mặt phân cách hai môi trường, còn góc khúc xạ là góc giữa tia khúc xạ và pháp tuyến đó. Theo định luật Snell, tỉ số giữa sin của góc tới và sin của góc khúc xạ bằng hằng số n, được gọi là chỉ số khúc xạ của môi trường. Công thức này có thể viết lại như sau:

sin(góc tới) / sin(góc khúc xạ) = n

Nếu góc tới tăng 2 lần, tức là góc tới mới bằng 2 lần góc tới cũ, ta có thể ký hiệu là:

góc tới mới = 2 * góc tới cũ

Để tính góc khúc xạ mới, ta thay vào công thức trên và giải ra được:

sin(góc khúc xạ mới) = n * sin(góc tới mới) / 2

⇒ sin(góc khúc xạ mới) = n * sin(2 * góc tới cũ) / 2

⇒ sin(góc khúc xạ mới) = n * (2 * sin(góc tới cũ) * cos(góc tới cũ)) / 2

⇒ sin(góc khúc xạ mới) = n * sin(góc tới cũ) * cos(góc tới cũ)

Do đó, để biết góc khúc xạ mới tăng bao nhiêu lần so với góc khúc xạ cũ, ta phải so sánh sin của hai góc đó. Ta có thể viết như sau:

(sin(góc khúc xạ mới) / sin(góc khúc xạ cũ)) = (n * sin(góc tới cũ) * cos(góc tới cũ)) / (n * sin(góc tới cũ))

⇒ (sin(góc khúc xạ mới) / sin(góc khúc xạ cũ)) = cos(góc tới cũ)

Vậy, tỉ số giữa góc khúc xạ mới và góc khúc xạ cũ bằng cos của góc tới cũ. Tùy vào giá trị của góc tới cũ mà tỉ số này có thể lớn hơn, bằng hoặc nhỏ hơn 1.

* Tóm tắt lại thì như sau:

Theo định luật Snell

μ = sini/sinr

Có: i = 2r

μ = sin2r/sinr

⇒ μ = 2sinrcosr/sinr

cos−1(μ/2) = r= i/2

⇒ i = 2cos−1(μ/2)

2. Định luật Snell:

Định luật Snell đưa ra mức khúc xạ và mối liên hệ giữa góc tới, góc khúc xạ và chiết suất của một cặp môi trường cho trước. Chúng ta biết rằng ánh sáng bị khúc xạ hoặc bị uốn cong khi truyền từ môi trường này sang môi trường khác. Định luật Snell dự đoán mức độ uốn cong. Nó còn được gọi là định luật khúc xạ. Năm 1621, Willebrord Snell phát hiện ra định luật khúc xạ, do đó gọi là định luật Snell.

Định luật Snell được định nghĩa là “Tỷ lệ giữa sin của góc tới và sin của góc khúc xạ là một hằng số, đối với ánh sáng có màu nhất định và đối với cặp môi trường cho trước”. Công thức định luật Snell được biểu diễn như sau:

μ = sini/sinr

Trong đó i là góc tới và r là góc khúc xạ. Giá trị không đổi này được gọi là chiết suất của môi trường thứ hai so với môi trường thứ nhất.

Sau đây là biểu diễn bằng sơ đồ:

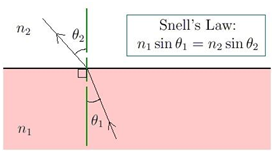
Công thức định luật Snell bắt nguồn từ nguyên lý Fermat. Nguyên lý Fermat phát biểu rằng “ánh sáng truyền đi theo con đường ngắn nhất và tốn ít thời gian nhất”.

Pháp tuyến trên bề mặt được dùng để đo góc mà tia khúc xạ tạo ra tại điểm tiếp xúc. n1 và n2 là hai môi trường khác nhau sẽ ảnh hưởng đến sự khúc xạ. là góc tới; là góc khúc xạ.

3. Thí nghiệm định luật Snell:

Để bắt đầu, hãy xem xét một cái đĩa hình bán nguyệt chứa đầy nước. Giả sử rằng một chùm tia laser hướng về phía mặt phẳng của đĩa ở đúng tâm của đĩa. Góc tới có thể được đo tại điểm tới. Tia này sẽ khúc xạ, uốn cong về phía pháp tuyến (vì ánh sáng truyền từ môi trường truyền nhanh sang môi trường truyền chậm). Khi tia sáng đi vào nước, nó truyền theo đường thẳng cho đến khi chạm tới ranh giới thứ hai. Tại ranh giới thứ hai, tia sáng tiến tới dọc theo pháp tuyến tới bề mặt cong. Tia không khúc xạ khi thoát ra vì góc tới là 0 độ. Do đó, tia sáng laser thoát ra cùng góc với tia sáng khúc xạ tạo ra ở ranh giới thứ nhất. Hai góc này có thể được đo và ghi lại. Góc tới của chùm tia laser có thể được thay đổi thành 5 độ và có thể thực hiện và ghi lại các phép đo mới. Quá trình này có thể được lặp lại cho đến khi thu thập được bộ dữ liệu hoàn chỉnh gồm các giá trị chính xác. 

Việc kiểm tra dữ liệu trên cho thấy rằng không có mối quan hệ tuyến tính rõ ràng giữa góc tới và góc khúc xạ. Ví dụ, việc tăng gấp đôi góc tới từ 40 độ lên 80 độ không dẫn đến việc tăng gấp đôi góc khúc xạ. Vì vậy, đồ thị của dữ liệu này sẽ không tạo ra một đường thẳng. Tuy nhiên, nếu vẽ sin của góc tới và sin của góc khúc xạ thì đồ thị sẽ là một đường thẳng, biểu thị mối quan hệ tuyến tính giữa sin của các góc quan trọng. Nếu hai đại lượng tạo thành một đường thẳng trên đồ thị thì mối quan hệ toán học có thể được viết dưới dạng y = m*x + b. Đồ thị của sin góc tới và sin góc khúc xạ được trình bày dưới đây.

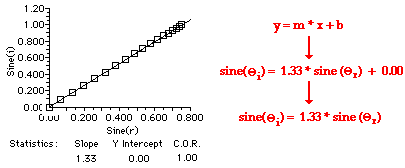
Phương trình liên hệ giữa góc tới (Θi) và góc khúc xạ (Θr) của ánh sáng truyền từ không khí vào nước được cho là

Quan sát thấy hằng số tỷ lệ trong phương trình này là 1,33 – chỉ số giá trị khúc xạ của nước. Có lẽ đó chỉ là sự trùng hợp ngẫu nhiên. Nhưng nếu thay đĩa bán trụ chứa đầy nước bằng đĩa Plexiglas bán trụ thì hằng số tỷ lệ sẽ là 1,51 – chỉ số giá trị khúc xạ của Plexiglas. Đây không chỉ là sự trùng hợp ngẫu nhiên. Mô hình tương tự sẽ dẫn đến ánh sáng truyền từ không khí vào bất kỳ vật liệu nào. Bằng thực nghiệm, người ta thấy rằng đối với một tia sáng truyền từ không khí vào một vật liệu nào đó, phương trình sau có thể được viết.

trong đó nmaterial = chiết suất của vật liệu

Nghiên cứu về sự khúc xạ của ánh sáng khi nó truyền từ vật liệu này sang vật liệu thứ hai mang lại mối quan hệ tổng quát giữa các sin của góc tới và góc khúc xạ. Mối quan hệ tổng quát này được thể hiện bằng phương trình sau:

trong đó Θi = góc tới

Θr = góc khúc xạ

ni  = chiết suất của môi trường tới

nr = chiết suất của môi trường khúc xạ

Mối quan hệ giữa góc tới, góc khúc xạ và chiết suất của hai môi trường được gọi là Định luật Snell. Định luật Snell áp dụng cho sự khúc xạ ánh sáng trong mọi tình huống, bất kể hai môi trường đó là gì.

4. Sử dụng định luật Snell để dự đoán giá trị góc:

Giống như bất kỳ phương trình vật lý nào, phương trình Định luật Snell được đánh giá cao nhờ khả năng dự đoán của nó. Nếu biết bất kỳ ba trong số bốn biến trong phương trình, biến thứ tư có thể dự đoán được nếu sử dụng các kỹ năng giải quyết vấn đề thích hợp. Điều này được minh họa trong hai ví dụ dưới đây.

Ví dụ

Trong hai ví dụ sau, hãy sử dụng định luật Snell, nút sin trên máy tính, thước đo góc và chỉ số giá trị khúc xạ để hoàn thành sơ đồ sau. Đo , tính và vẽ tia khúc xạ với góc khúc xạ đã tính.

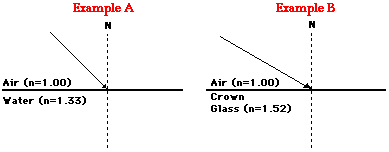
Hướng dẫn:

Trong bài toán ví dụ này, góc khúc xạ là biến cần xác định. Các chỉ số khúc xạ (ni và nr) được cho trước và góc tới có thể đo được. Với ba trong số bốn biến đã biết, việc thay thế định luật Snell sau đó bằng thao tác đại số sẽ dẫn đến câu trả lời.

Lời giải:

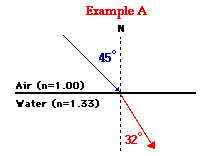
* Ví dụ A

Đầu tiên, dùng thước đo góc để đo góc tới. Một phép đo thích hợp sẽ là một góc gần 45 độ.

Thứ hai, liệt kê tất cả các giá trị đã biết và giá trị chưa biết mà bạn muốn giải:

Thứ ba, liệt kê các phương trình có liên quan:

Thứ tư, thay thế các giá trị đã biết vào phương trình và vận dụng đại số vào phương trình để giải biến chưa biết – Θr.

1,00 * sin (45 độ) = 1,33 * sin (Θr)

⇒ 0,7071 = 1,33 * sin (Θr)

⇒ 0,532 = sin (Θr)

⇒ sin-1 (0,532) = sin-1 ( sin Θr)

⇒ 32,1 độ = Θr

Đại số thích hợp sẽ cho kết quả là góc khúc xạ là 32,1 độ. 

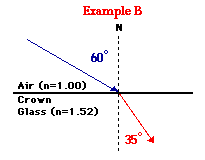
* Ví dụ B:

Đo góc tới – góc hợp bởi tia pháp tuyến và tia tới. Là khoảng 60 độ.

Liệt kê tất cả các giá trị đã biết và giá trị chưa biết mà bạn muốn giải:

Thay thế vào phương trình định luật Snell và thực hiện các phép toán đại số cần thiết để giải:

1,00 • sin(60 độ) = 1,52 • sin(Θr)

⇒ 0,8660 = 1,52 • sin(Θr)

⇒ 0,570 = sin(Θr)

⇒ 34,7 độ = Θr

Bây giờ vẽ tia khúc xạ hợp một góc 34,7 độ so với pháp tuyến