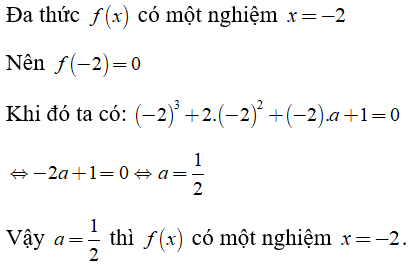Rút gọn đa thức là một kỹ năng quan trọng trong toán học, giúp cho việc tính toán và phân tích đa thức trở nên dễ dàng hơn. Sau đây là bài viết hướng dẫn cách thu gọn đa thức nhanh có bài tập ôn tập để các bạn học sinh tham khảo.
Mục lục bài viết
1. Cách thu gọn đa thức cơ bản:
* Cách 1:
Đơn giản hóa đa thức là quá trình biến đổi một đa thức thành một dạng tương đương nhưng ngắn gọn và dễ tính toán hơn. Để đơn giản hóa đa thức, ta cần thực hiện các bước sau:
– Bước 1: Phân loại các hạng tử của đa thức theo số mũ giảm dần của biến số.
– Bước 2: Rút gọn các hạng tử có cùng số mũ của biến số bằng cách cộng hoặc trừ các hệ số tương ứng.
– Bước 3: Nếu có thể, áp dụng các công thức nhân, chia hoặc lũy thừa để rút gọn thêm đa thức. 7x2
Ví dụ: Đơn giản hóa đa thức x2 – 6x + 5
Ta có thể sử dụng phương pháp phân tích nhân tử để viết nó thành:
(x – 5)(x – 1)
Ta có thể kiểm tra bằng cách nhân lại hai nhân tử và thu được lại đa thức ban đầu. Ta có thể sử dụng phương pháp bình phương hoàn chỉnh để viết nó thành:
(x – 3)2– 4
Ta có thể kiểm tra bằng cách mở ngoặc và thu được lại đa thức ban đầu. Để tìm nghiệm của đa thức, giải hai phương trình sau:
x – 5 = 0
x – 1 = 0
Hoặc:
x – 3 = ±√4
Ta thu được nghiệm là x = 5 hoặc x = 1.
* Cách 2:
Đa thức phải luôn được đơn giản hóa càng nhiều càng tốt. Điều đó có nghĩa là bạn phải cộng tất cả các hạng tử tương tự lại với nhau.
Các hạng tử giống nhau có hai điểm chung:
– Các biến tương tự
– Các biến có cùng số mũ
Ví dụ:
– 5x và 6x giống nhau vì cả hai đều có biến x và không có số mũ
– 8y và 8x không giống nhau vì chúng có các biến số khác nhau
– 5x2 và 7x2 giống nhau vì cả hai đều có x và cả hai x đều có cùng số mũ
– 2x2 và 5x không giống vì chúng không có cùng số mũ
– 5y và 10 không giống nhau vì 10 không có y
Việc biết hạng tử giống nhau hay không là quan trọng vì chỉ có thể thêm hoặc bớt các hạng tử giống nhau.
Để thêm các hạng tử tương tự:
– Đảm bảo các hạng tử giống như các hạng tử. Nếu không, chúng không thể được thêm vào.
– Cộng các hệ số (các số).
– Giữ (các) biến giống nhau.
Ví dụ:
– 3x + 5x: Đây là những số hạng giống nhau nên chúng ta có thể cộng chúng lại. Cộng các số (3 + 5 = 8) và giữ nguyên biến. Lưu ý câu trả lời chỉ là 8x chứ không phải 8x2.
Đáp án: 8x
– 5y – 7y + 3 = -2y + 3
5y và -7y giống nhau nên chúng có thể cộng lại với nhau. 5 + (-7) = -2
-2y và 3 không giống các số hạng nên bạn không thể cộng chúng lại với nhau.
Đáp án: -2y+3
Đa thức này có hai tập hợp số hạng giống nhau. Thêm chúng riêng biệt.
5x – 2x = 3x.
Câu trả lời cuối cùng là 12x2 + 3x vì 12x2 và 3x không giống nhau (chúng có số mũ khác nhau).
2. Cách thu gọn phân số đa thức:
Một biểu thức hữu tỉ giống như một phân số trong đó cả tử số và mẫu số đều là đa thức. Tương tự, phân số đa thức ở dạng tỷ lệ của hai đa thức như 
trong đó không được phép chia hết cho 0, như .png)
. Quy tắc tương tự của phân số được áp dụng ở đây như phân số đa thức, điểm khác biệt là cả tử số và mẫu số đều là đa thức. Nhiều phép toán khác nhau có thể được thực hiện giống như chúng ta thực hiện trong số học đơn giản như cộng, chia, nhân và trừ.
Phân số đa thức là biểu thức của một đa thức chia cho một đa thức khác. Đặt P(x) và Q(x), trong đó Q(x) không thể bằng 0.
Phân số đa thức có thể được đơn giản hóa bằng đa thức có trong tử số hoặc mẫu số bằng cách phân tích và rút gọn chúng thành số hạng thấp nhất. Ví dụ: phân số .png)
sẽ được rút gọn thành số hạng thấp nhất là .png)
. Tương tự, phân số .png)
sẽ được đơn giản hóa thành .png)
bằng cách phân tích cả tử số và mẫu số và rút gọn về số hạng nhỏ nhất.
2.1. Đa thức trong tử số hoặc mẫu số:
Bước 1. Để thu gọn đa thức trong tử số hoặc mẫu số, trước tiên hãy phân tích đa thức trong tử số hoặc mẫu số.
Bước 2. Sau đó, đơn giản hóa phân số thành số hạng nhỏ nhất bằng cách loại bỏ mọi đơn thức hoặc đa thức chung tồn tại ở cả tử số và mẫu số, nếu có thể.
Bước 3. Cuối cùng, viết lại các số hạng bằng cách nhân bất kỳ đơn thức hoặc đa thức nào còn nằm trong tử số hoặc mẫu số.
.png)
Lời giải:
Bước 1. Phân tích đa thức thành nhân tử hoàn toàn ở mẫu số.
= .png)
= .png)
Bước 2. Rút gọn phân số về số hạng tối giản bằng cách loại bỏ các đơn thức hoặc đa thức chung tồn tại ở cả tử số và mẫu số.
= .png)
Bước 3. Viết lại biểu thức ở mẫu số bằng cách sử dụng thuộc tính phân phối.
= .png)
2.2. Đa thức trong tử số và mẫu số:
Bước 1. Để thu gọn đa thức trong tử số và mẫu số, hãy phân tích đa thức hoàn toàn trong tử số và mẫu số.
Bước 2. Sau đó đơn giản hóa phân số thành số hạng nhỏ nhất bằng cách loại bỏ mọi đơn thức hoặc đa thức chung tồn tại ở cả tử số và mẫu số.
Bước 3. Cuối cùng, nhân mọi thừa số còn lại trong tử số hoặc mẫu số.
Ví dụ: Rút gọn phân số .png)
Lời giải:
Bước 1 Phân tích đa thức thành nhân tử hoàn toàn ở tử số và mẫu số.
= .png)
= .png)
Bước 2 Rút gọn phân số về số hạng nhỏ nhất bằng cách loại bỏ các đơn thức hoặc đa thức chung tồn tại ở cả tử số và mẫu số.
= .png)
Bước 3. Viết lại biểu thức ở tử số bằng cách sử dụng thuộc tính phân phối
= .png)
3. Bài tập thu gọn đa thức có đáp án:
Bài 1: Rút gọn phân số .png)
Lời giải:
Bước 1. Phân tích đa thức thành nhân tử hoàn toàn ở mẫu số.
= .png)
Bước 2. Rút gọn phân số về số hạng tối giản bằng cách loại bỏ các đơn thức hoặc đa thức chung tồn tại ở cả tử số và mẫu số.
= .png)
Bài 2: Rút gọn phân số .png)
Lời giải:
Bước 1 Phân tích đa thức thành nhân tử hoàn toàn ở tử số và mẫu số.
= .png)
= .png)
Bước 2 Rút gọn phân số về số hạng nhỏ nhất bằng cách loại bỏ các đơn thức hoặc đa thức chung tồn tại ở cả tử số và mẫu số.
= .png)
Bước 3. Viết lại biểu thức ở mẫu số bằng cách sử dụng thuộc tính phân phối
= .png)
Bài 3: Thu gọn đa thức 3x – 4y + 8x
Lời giải:
Để thu gọn đa thức 3x – 4y + 8x, ta cần tìm các hạng tử có cùng biến số và cộng hoặc trừ chúng lại. Trong trường hợp này, ta có hai hạng tử có biến số x là 3x và 8x. Ta cộng chúng lại để được 11x. Hạng tử -4y không có biến số nào giống nó nên ta giữ nguyên. Kết quả là đa thức thu gọn là 11x – 4y.
Bài 4: Thu gọn đa thức -2x2 + 7y2 – 9y
Lời giải:
Để thu gọn đa thức, ta cần áp dụng các quy tắc cộng, trừ và nhân các số hạng có cùng bậc.
Ta nhận thấy có hai số hạng có cùng bậc là -2y2 và 7y2. Ta có thể cộng hai số hạng này lại để được:
(-2 + 7)y2 – 9y
Sau khi tính toán, ta được:
5y2 – 9y
Đây là đa thức đã được thu gọn.
Bài 5: Thu gọn đa thức 3x – 5y + 9y + 4x
Ta nhận thấy có hai số hạng có cùng bậc là 3x và 4x, và hai số hạng khác có cùng bậc là -5y và 9y. Ta có thể cộng các số hạng cùng bậc lại để được:
(3 + 4)x + (-5 + 9)y
Sau khi tính toán, ta được:
7x + 4y
Đây là đa thức đã được thu gọn.
Bài 6: Thu gọn đa thức 3x + x + 3x
Lời giải:
Ta thấy có ba hạng tử có biến số là x và bậc là 1, nên ta cộng các hệ số của chúng lại được:
(3 + 1 + 3)x = 7x
Vậy đa thức đã được thu gọn là 7x.
Bài 7: Rút gọn đa thức 5y + 1
Lời giải:
Ta thấy chỉ có một hạng tử có biến số là y và bậc là 1, nên ta không thể cộng hoặc trừ gì thêm. Vậy đa thức đã được thu gọn là 5y + 1.
