Để có thể giải hệ phương trình đối xứng loại 2 và tìm ra các giá trị của các biến thỏa mãn điều kiện cho trước, các em học sinh cần nắm vững những kiến thức lý thuyết cơ bản. Dưới đây là bài viết về chủ đề: Hướng dẫn cách giải hệ phương trình đối xứng loại 2 lớp 9, mời bạn đọc theo dõi.
Mục lục bài viết
1. Hướng dẫn cách giải hệ phương trình đối xứng loại 2 lớp 9:
Hệ phương trình đối xứng loại 2 là một dạng đặc biệt của hệ phương trình đối xứng, nổi bật với tính chất cân bằng và sự hoán đổi giữa các biến. Điều này được thể hiện qua cấu trúc của nó, trong đó hai phương trình chính là biểu diễn của một hàm hai biến đối với các biến x và y.
Để hiểu rõ hơn về hệ phương trình đối xứng loại 2, ta cần xem xét cấu trúc cụ thể của nó. Hệ phương trình này thường được biểu diễn theo dạng:
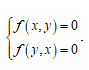
Ở đây, f(x,y) và f(y,x) là hai phương trình trong hệ, mỗi phương trình thể hiện một mối quan hệ giữa các biến x và y. a là hằng số, thường được gọi là hệ số, không bằng không.
Một cách tổng quát, để giải hệ phương trình đối xứng loại 2, ta có thể thực hiện các bước sau:
Bước 1: Gán một biến tham số, thường được ký hiệu là t, cho một trong hai biến x hoặc y. Giả sử chúng ta gán x=t.
Bước 2: Sử dụng phương trình f(y,x)=a để tìm giá trị của biến còn lại, trong trường hợp này là y, dựa trên giá trị đã chọn của biến tham số t.
Bước 3: Thay giá trị của biến đã tìm được vào phương trình f(x,y)=a.
Bước 4: Giải phương trình thu được để tìm giá trị của biến tham số t.
Bước 5: Thay giá trị của t đã tìm được vào phương trình f(y,x)=a để tìm giá trị của biến còn lại, trong trường hợp này là y.
Bước 6: Kết quả cuối cùng là cặp giá trị (x,y) thỏa mãn đồng thời cả hai phương trình f(x,y)=a và f(y,x)=a.
Qua các bước trên, ta có thể giải hệ phương trình đối xứng loại 2 và tìm ra các giá trị của các biến thỏa mãn điều kiện cho trước. Điều này có thể áp dụng trong nhiều lĩnh vực khác nhau, từ toán học đến vật lý và kỹ thuật.
2. Ví dụ minh họa:
Ví dụ 1: Giải hệ phương trình:
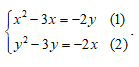
Hướng dẫn:
Trừ từng vế của hai phương trình ta được:
x^2 – y^2 – 3x + 3y = -2y + 2x
(x – y)(x + y) – 5(x – y) = 0
(x – y)(x + y – 5) = 0
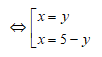
Với x = y thay vào (1) ta được:
y^2 – y = 0 y(y-1) = 0 
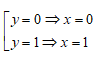
Với x = 5 – y thay vào (2) ta được:
y^2 – 3y = -2(5 – y) y^2 – 3y = -10 + 2y
y^2 – 5y + 10 = 0 (*)
Ta có = 25 – 4.10 = 25 – 40 = -15 < 0
Suy ra pt () vô nghiệm
Vậy nghiệm của hệ phương trình đã cho là:
(x; y) thuộc {(0;0), (1;1)}.
Ví dụ 2: Giải hệ phương trình
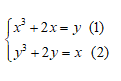
Hướng dẫn:
Trừ từng vế của hai phương trình ta được:
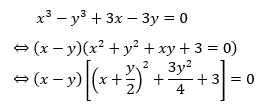
Ví dụ 3: Giải hệ phương trình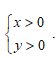 
Hướng dẫn:
Vì vế phải của mỗi phương trình đều dương nên ta có
Ta có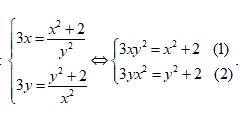 
Trừ từng vế của hai phương trình (1) và (2) ta sẽ được:
3xy^2 – 3yx^2 = x^2 – y^2
3xy (y – x) = (x – y)(x + y)
(x – y)( 3xy + x + y) = 0
Vì x> 0, y> 0 => 3xy + x + y > 0 => x = y
Với x = y thay vào (1) ta được
3x^3 – x^2 – 2 = 0
(x – 1) (3x^2 + 2x + 2) = 0
x = 1 => y = 1
Vậy nghiệm của hệ phương trình là (1;1)
3. Bài tập trắc nghiệm kèm lời giải:
Câu 1: Hệ phương trình sau có bao nhiêu nghiệm: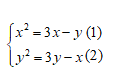 
A. 1
B. 2
C. 3
D. 4
Lời giải
Ta sẽ lấy phương trình (1) trừ đi phương trình (2) và sẽ được:
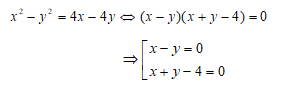
Trường hợp 1: x = y. Ta sẽ thay x = y vào phương trình số (1) và sẽ được
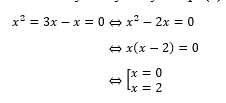
Suy ra hệ có 2 nghiệm chính là: (0;0), (2;2)
Trường hợp 2: x + y – 4 = 0. Ta thay y = 4 – x vào phương trình số (1) và sẽ được:
x^2 – 4x + 4 = 0 <=> (x – 2)^2 = 0 => x = 2
Với x = 2 => y = 2. Suy ra hệ có nghiệm là (2;2)
Vậy hệ phương trình có 2 nghiệm là (0;0), (2;2).
Vậy đáp án đúng sẽ là B.
Câu 2: Hệ phương trình sau có bao nhiêu nghiệm: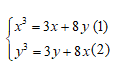
A. 4
B. 2
C. 3
D. 5
Lời giải
Ta sẽ lấy phương trình (1) trừ đi phương trình (2) và sẽ được:
x^3 – y^3 = – 5x + 5y
<=> (x – y) (x^2 + xy + y^2 + 5) = 0
Trường hợp 1: x – y = 0. Ta sẽ thay x = y vào phương trình số (1) và sẽ được
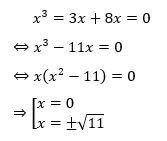
Suy ra hệ có 2 nghiệm chính là: (0;0), 
Trường hợp 2: Ta sẽ có:
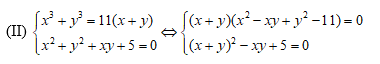
Đặt: x + y = S, xy = P, S^2 >= 4P
Suy ra ta có:
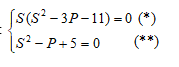
Từ phương trình số (*) ta sẽ có:
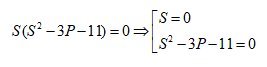
Với S = 0 thì P = 5 (loại)
Ta có (II):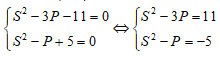 
Ta sẽ lấy phương trình (3) trừ đi phương trình (4) và sẽ được:
-2P = 16 <=> P = -8
Với P = -8 => S^2 = -8 – 5 = -13 (vô lý)
Từ đó suy ra hệ phương trình (II) vô nghiệm
Vậy hệ phương trình có 3 nghiệm là (0;0), 
Vậy đáp án đúng sẽ là C.
Câu 3: Hệ phương trình sau có bao nhiêu nghiệm: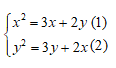 
A. 1
B. 2
C. 3
D. 4
Lời giải
Ta sẽ lấy phương trình (1) trừ đi phương trình (2) và sẽ được:
x^2 – y^2 = x – y
<=> (x – y) (x + y – 1) = 0
Trường hợp 1: x – y = 0. Ta sẽ thay x = y vào phương trình số (2) và sẽ được
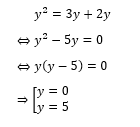
Suy ra hệ có 2 nghiệm chính là: (0;0), (5;5)
Trường hợp 2: Ta sẽ có: x + y – 1 = 0. Thay y = 1 – x vào phương trình số (1) ta được:
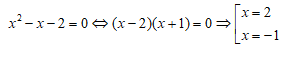
Với x = 2 => y = -1 và x = -1 => y = 2
Từ đó suy ra hệ phương trình có 2 nghiệm là: (2;-1), (-1;2)
Vậy hệ phương trình có 4 nghiệm là (0;0), (5;5), (2; -1), (-1;2)
Vậy đáp án đúng sẽ là D.
Câu 4: Hệ phương trình sau có bao nhiêu nghiệm: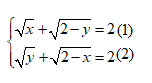 
A. 1
B. 2
C. 3
D. 4
Lời giải
Điều kiện: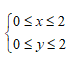 
Ta sẽ lấy phương trình (1) trừ đi phương trình (2) và sẽ được:
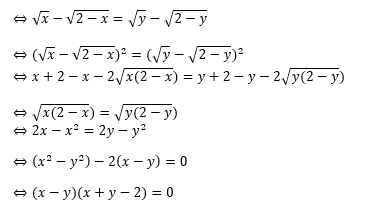
Trường hợp 1: x – y = 0. Ta sẽ thay x = y vào phương trình số (1) và sẽ được
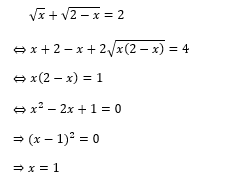
Suy ra hệ có nghiệm chính là: (1;1).
Trường hợp 2: Ta sẽ có: x + y – 2 = 0. Thay y = 2 – x vào phương trình số (1) ta được:
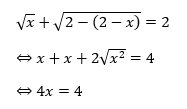
=> x = 1 (thỏa mãn)
Với x = 1 => y = 1
Từ đó suy ra hệ phương trình có 2 nghiệm là: (1;1),
Vậy hệ phương trình có 1 nghiệm là (1;1).
Vậy đáp án đúng sẽ là A.
Câu 5: Hệ phương trình sau có bao nhiêu nghiệm: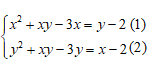 
A. 4
B. 3
C. vô số nghiệm
D. vô nghiệm
Lời giải
Ta sẽ lấy phương trình (1) trừ đi phương trình (2) và sẽ được:
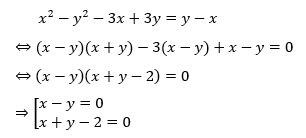
Trường hợp 1: x – y = 0. Ta sẽ thay x = y vào phương trình số (1) và sẽ được
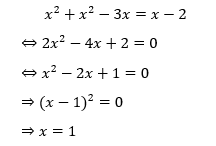
Suy ra hệ có nghiệm chính là: (1;1).
Trường hợp 2: Ta sẽ có: x + y – 2 = 0.
Thay y = 2 – x vào phương trình số (1) ta được:
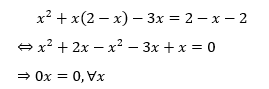
Từ đó suy ra hệ phương trình có nghiệm là:
Vậy hệ phương trình có 1 nghiệm là
Vậy đáp án đúng sẽ là C.
Câu 6: Hệ phương trình sau: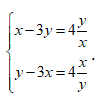 
. Khẳng định nào sau đây đúng ?
A. Hệ phương trình có vô số nghiệm.
B. Hệ phương trình có 3 nghiệm.
C. Hệ phương trình có 4 nghiệm.
D. Hệ phương trình có 1 nghiệm.
Lời giải
Điều kiện
Ta sẽ lấy phương trình (1) trừ đi phương trình (2) và sẽ được:
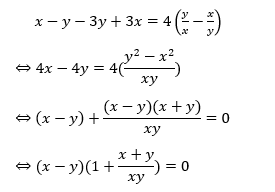
Trường hợp 1: x – y = 0. Ta sẽ thay x = y vào phương trình số (1) và sẽ được:
-2x = 4 => x = -2
Với x = -2 => y = -2.
Suy ra hệ có nghiệm chính là: (-2;-2).
Trường hợp 2:
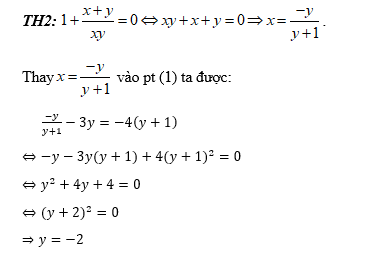
Với y = -2 => x = -2 (thỏa mãn)
Từ đó suy ra hệ phương trình có nghiệm là: (-2;-2)
Vậy hệ phương trình có 1 nghiệm là (-2;-2)
Vậy đáp án đúng sẽ là D.
THAM KHẢO THÊM:
