Hình lăng trụ là gì? Lăng trụ đều là gì? Tính chất và bài tập?

1. Hình lăng trụ là gì? Lăng trụ đều là gì?

Hình lăng trụ là một hình đa diện bao gồm hai mặt đáy là hai đa giác bằng nhau và nằm trên hai mặt phẳng song song, các bên mặt bên đều là hình bình hành, các cạnh bên song song và bằng nhau. Ngoài ra, hai mặt đáy này có thể là hình vuông, hình chữ nhật, hình tam giác…

Hình lăng trụ là một hình khối không gian được tạo thành bởi:

• Hai đáy: Là hai đa giác bằng nhau và song song với nhau. Hình dạng của đáy có thể là bất kỳ đa giác nào (tam giác, tứ giác, ngũ giác,…)
• Các mặt bên: Là các hình bình hành.
• Các cạnh bên: Là các đoạn thẳng nối các đỉnh tương ứng của hai đáy, chúng song song và bằng nhau

2. Công thức tính thể tích và diện tích hình lăng trụ:

Thể tích hình lăng trụ

Thể tích hình lăng trụ bằng diện tích của mặt đáy nhân với chiều cao hình lăng trụ hoặc là khoảng cách giữa hai mặt đáy.

V = B.h

Trong đó:

• B là diện tích mặt đáy của hình lăng trụ 
• h là chiều cao của của hình lăng trụ 
• V là thể tích hình lăng trụ

Diện tích xung quanh hình lăng trụ

Diện tích xung quanh hình lăng trụ bằng chu vi đáy hoặc tổng diện tích các mặt bên nhân với chiều cao của hình lăng trụ.

Sxq = 2p.h

Trong đó:

• p là nửa chu vi đáy 
• h là chiều cao của hình lăng trụ 
• Sxq là diện tích xung quanh của hình lăng trụ 

Diện tích toàn phần hình lăng trụ

Diện tích toàn phần hình lăng trụ bằng tổng diện tích hai đáy và tổng các diện tích xung quanh.

Stp = 2S + Sxq

Trong đó:

• S là diện tích đa giác ở mặt đáy 
• Sxq là diện tích xung quanh của hình lăng trụ 
• Stp là diện tích toàn phần của hình lăng trụ

3. Hình lăng trụ đều là gì?

Định nghĩa: Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều. Theo đó, hình lăng trụ đứng là hình lăng trụ có cạnh bên vuông góc với mặt đáy.

Ví dụ: Các lăng trụ đều là hình lăng trụ tam giác đều, hình lăng trụ tứ giác đều, hình lăng trụ ngũ giác đều và hình lăng trụ lục giác đều.

Tính chất:

• Hai mặt đáy là hai đa giác đều bằng nhau, vì vậy các cạnh đáy cũng sẽ bằng nhau. 
• Các cạnh bên vuông góc với mặt đáy. 
• Các mặt bên của hình lăng trụ là các hình chữ nhật.

4. Các hình lăng trụ đều thường gặp:

• Hình lăng trụ tam giác đều là hình lăng trụ có hai mặt đáy là hai hình tam giác đều. 

• Hình lăng trụ tứ giác đều là hình lăng trụ đều có hai mặt đáy là hình vuông.

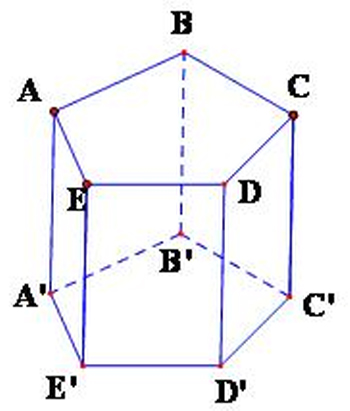
• Hình lăng trụ ngũ giác đều là hình lăng trụ đều có hai mặt đáy là hình ngũ giác.

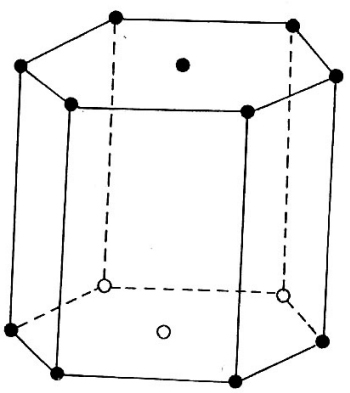
• Hình lăng trụ lục giác đều là hình lăng trụ đều có hai mặt đáy là hình lục giác.

5. Bài tập vận dụng:

5.1. Bài tập trắc nghiệm:

Câu 1: Hình lăng trụ đều là hình lăng trụ được tạo bởi:

A. Hai mặt đáy là hai đa giác đều bằng nhau, mặt bên là các hình bình hành.

B. Hai mặt đáy là hai đa giác, mặt bên là các hình chữ nhật bằng nhau.

C. Hai mặt đáy là hai đa giác đều bằng nhau, mặt bên là các hình chữ nhật bằng nhau

D. Hai mặt đáy là hai đa giác đều bằng nhau, mặt bên là các hình chữ nhật.

Hướng dẫn giải: Đáp án C

Câu 2: Một nhà hàng có kế hoạch làm một bể cá bằng kính, dự định là sử dụng hết 6,5 m² kính. Bể cá này có hình dạng là hình hộp chữ nhật không có nắp, kích thước chiều dài gấp đôi chiều rộng. Tính dung tích lớn nhất của bể cá có thể chứa được?

A. 1,50 m³

B. 1,15 m³

C. 1,23 m³

D. 1,45 m³

Hướng dẫn giải: Đáp án A

Câu 3: Cho một hình lăng trụ ABC.A’B’C’ có mặt đáy ABC là tam giác đều có cạnh bằng a. Điểm A’ có hình chiếu vuông góc lên mặt phẳng (ABC) và trùng với tâm O của đường tròn ngoại tiếp tam giác ABC. Biết cạnh A’O có kích thước bằng a. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a.

A. a³/12

B. (a³√3)/ 6

C. (a³√3)/ 12

D. a³/2

Hướng dẫn giải: Đáp án C

Câu 4: Biết tất cả các cạnh bằng a. Tính thể tích của khối lăng trụ tam giác đều đó.

A. V = √3a³/6

B. V= √3a³/4

C. V = √3a³/3

D. V= √2a³/4

Hướng dẫn giải: Đáp án B

Câu 5: Cho một khối lăng trụ có diện tích đáy bằng 4a² và có chiều cao bằng a. Tính thể tích của khối lăng trụ đã cho theo a.

A. V = 4a³

B. V = a³

C. V = 2a²

D. 1/2a²

Hướng dẫn giải: Đáp án A.

Câu 6: Một hình bát diện đều có các mặt bên là hình gì?

A. Hình tam giác đều

B. Hình vuông

C. Hình chữ nhật

D. Hình tam giác cân

Hướng dẫn giải: Đáp án A

5.2. Bài tập tự luận:

Bài tập 1: Cho hình lăng trụ có đáy là hình tam giác vuông. Biết hai cạnh góc vuông lần lượt là 6 và 7, chiều cao của hình lăng trụ là 8. Tính thể tích hình lăng trụ đó. 

Hướng dẫn giải:

Diện tích đáy tam giác của hình lăng trụ là: S = ( 6. 7 )/ 2 = 21

Thể tích hình lăng trụ đó là: V = S. h = 21. 8 = 168.

Kết luận: Vậy thể tích hình lăng trụ đã cho là bằng 168

Bài tập 2: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh bằng 10. Biết chiều cao AA’ của hình lăng trụ bằng 5. Tính thể tích hình lăng trụ đó.

Hướng dẫn giải:

Kẻ đường cao AH của tam giác ABC.

Vì tam giác ABC là tam giác đều nên H trở thành trung điểm của BC.

=> BH = CH = BC / 2 = 10/ 2 = 5 

Vì tam giác ABH vuông tại H nên theo định lý Pytago ta có: AH = 5√75

Diện tích đáy hình lăng trụ là: SABC = ( AH.BC )/ 2 = 5√(75) 

Thể tích hình lăng trụ tam giác đều đó là: V = S. h = SABC. AH = 5√75. √75 = 375.

Kết luận: Vậy thể tích hình lăng trụ tam giác đều ABC.A’B’C’ là bằng 375

Bài tập 3: Cho hình lăng trụ có mặt đáy là hình tam giác vuông là có cạnh góc vuông lần lượt là 3 và 6. Biết thể tích của hình lăng trụ là 72. Tính chiều cao của hình lăng trụ.

Hướng dẫn giải:

Diện tích đáy hình lăng trụ là: S = ( 3. 6 )/ 2 = 9

Chiều cao của hình lăng trụ đó là: h = V/ S = 72/ 9 = 8

Kết luận: Hình lăng trụ đã cho có chiều cao bằng 8

Bài tập 4: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều, AH là đường cao. Biết hình lăng trụ có thể tích và chiều cao lần lượt là 80 và 5. Tính chiều cao AH của tam giác đều ABC.

Hướng dẫn giải:

Theo đề bài ta có:

Diện tích tam giác ABC là: SABC = V/ h = 90/ 3 = 30 

Vì tam giác ABC là tam giác đều mà AH là đường cao nên H là trung điểm của BC.

Gọi tam giác đều ABC có cạnh bằng a.

=> BH = CH = 1/2BC = a/2

Vì tam giác ABH vuông tại H, theo định lý Pytago ta có: AH = a√(3/4)

Ta có: SABC = ( AH. BC )/ 2 = 30 => AH. BC = 60 <=> a√(3/4). a = 60

=> a = √80 => AH = √60

Kết luận: Vậy tam giác ABC có chiều cao AH bằng √60

Bài tập 5: Cho hình lăng trụ ABC.A’B’C’ có đáy là hình tam giác ABC. AH là đường cao tam giác ABC. Biết AH bằng 3, BC bằng 4, và thể tích hình lăng trụ bằng 42. Tính chiều cao của hình lăng trụ.

Hướng dẫn giải:

Diện tích tam giác ABC là: SABC = ( AH. BC )/ 2 = ( 3. 4 )/ 2 = 6 

Chiều cao của hình lăng trụ ABC.A’B’C’ là: h = V/ SABC = 42/ 6 = 7

Kết luận: Vậy chiều cao của hình trụ đã cho là 7

Bài tập 6: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại A. Biết AB bằng 4, thể tích và chiều cao hình lăng trụ lần lượt là 36 và 6. Tính cạnh AC.

Hướng dẫn giải:

Diện tích đáy tam giác ABC là: SABC = V/ h = 36/ 6 = 6

Vì tam giác ABC vuông tại A mà diện tích của tam giác bằng 6 nên ta có:

SABC = ( AB. AC )/ 2 = 6 => AC = 12/ AB = 12/ 4 = 3

Kết luận: Vậy cạnh AC của tam giác ABC là 3

Bài tập 7: Cho hình lăng trụ ABC.A’B’C’ có AH là đường cao của đáy tam giác ABC. Biết rằng cạnh AH bằng 3, cạnh BC bằng 4 và thể tích hình lăng trụ đã cho bằng 24. Tính chiều cao của hình lăng trụ đã cho và cạnh BC’.

Hướng dẫn giải:

Diện tích đáy của hình lăng trụ đã cho là: SABC = ( 3. 4 )/2 = 6

Chiều cao của hình lăng trụ đã cho là: h = V/ SABC = 24/ 6 = 4 => AA’ = BB’ = CC’ = 4

Vì tam giác BCC’ vuông tại C nên theo định lý pytago ta có: (BC’)2 = (BC)2 + (CC’)2 = 32 BC’ = √(32)

Kết luận: Vậy chiều cao hình lăng trụ đã cho bằng 4 và cạnh BC’ bằng √(32)