Hình chóp tam giác đều là gì? Phân biệt với hình tứ diện đều?

1. Hình chóp tam giác đều là gì?

1.1. Định nghĩa hình chóp tam giác đều:

Hình chóp tam giác đều là một hình chóp có đáy là tam giác đều, các mặt bên đều bằng nhau và hình chiếu của đỉnh chóp xuống đáy trùng với tâm của tam giác đều. Hình chóp tam giác đều có nhiều ứng dụng trong kiến trúc, đồ họa máy tính, đo lường và trò chơi.

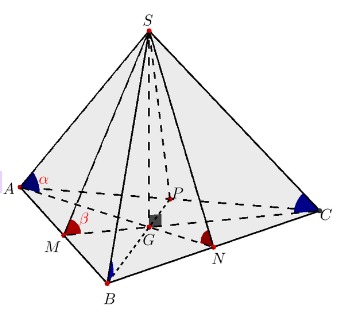
1.2. Tích chất của hình chóp tam giác đều:

Hình chóp tam giác đều có các tính chất sau:

– Đáy là tam giác đều có cạnh bằng a

– Các cạnh bên đều bằng nhau và bằng h

– Các mặt bên là tam giác cân, không nhất thiết là tam giác đều

– Chân đường cao trùng với tâm đáy, có chiều dài bằng H

– Góc được tạo bởi mặt bên và mặt đáy đều bằng nhau

– Góc được tạo bởi cạnh bên và mặt đáy đều bằng nhau

– Đỉnh là điểm giao nhau của các cạnh bên của chóp.

– Góc đỉnh là góc giữa hai cạnh bên gần đỉnh của chóp.

– Chiều cao là đoạn thẳng nối từ đỉnh của chóp đến mặt phẳng đáy vuông góc với mặt phẳng đáy.

Chú ý:

+ Tâm của tam giác đều là giao điểm 3 đường trung tuyến, cũng là đường cao, trung trực và phân giác trong.

+ Tâm của hình vuông chính là giao điểm hai đường chéo.

1.3. Công thức về hình chóp tam giác đều:

Để tính diện tích và thể tích của hình chóp tam giác đều, ta có các công thức sau:

– Diện tích mặt đáy: Sđ = (a^2 x √3) / 4

– Diện tích toàn phần: St = Sđ + 3 x (ah / 2)

– Thể tích: V = (Sđ x H) / 3

Trong đó, a là cạnh của tam giác đều, h là cạnh bên của hình chóp, H là chiều cao của hình chóp.

Ví dụ: 

Bài tập 1: Cho hình chóp tam giác đều SABC có cạnh đáy bằng 6 cm, cạnh bên bằng 10 cm. Tính diện tích toàn phần và thể tích của hình chóp.

Lời giải:

– Ta có: a = 6 cm, h = 10 cm

– Tính diện tích mặt đáy: Sđ = (6^2 x √3) / 4 = 9√3 cm^2

– Tính chiều cao của hình chóp: H = √(h^2 – (a/√3)^2) = √(100 – 12) = 6√2 cm

– Tính diện tích toàn phần: St = Sđ + 3 x (ah / 2) = 9√3 + 3 x (6 x 10 / 2) = 9√3 + 90 cm^2

– Tính thể tích: V = (Sđ x H) / 3 = (9√3 x 6√2) / 3 = 18√6 cm^3

Bài tập 2: Cho hình chóp tam giác đều SABC có cạnh đáy bằng 4 cm, chiều cao bằng 6 cm. Tính diện tích toàn phần và thể tích của hình chóp.

Lời giải:

– Ta có: a = 4 cm, H = 6 cm

– Tính diện tích mặt đáy: Sđ = (4^2 x √3) / 4 = 4√3 cm^2

– Tính cạnh bên của hình chóp: h = √(H^2 + (a/√3)^2) = √(36 + 16/3) = 2√13 cm

– Tính diện tích toàn phần: St = Sđ + 3 x (ah / 2) = 4√3 + 3 x (4 x 2√13 / 2) = 4√3 + 12√13 cm^2

– Tính thể tích: V = (Sđ x H) / 3 = (4√3 x 6) / 3 = 8√3 cm^3

2. Phân biệt hình chóp tam giác đều với hình tứ diện đều:

Hình chóp tam giác đều là một hình chóp có đáy là tam giác đều và các mặt bên là tam giác cân. Hình tứ diện đều là một trường hợp đặc biệt của hình chóp tam giác đều, khi mà các mặt bên cũng là tam giác đều. Để phân biệt hai loại hình này, ta có thể dựa vào các đặc điểm sau:

– Số mặt: Hình chóp tam giác đều có 4 mặt, trong đó 1 mặt là đáy và 3 mặt là bên. Hình tứ diện đều có 4 mặt, tất cả đều là tam giác đều.

– Số cạnh: Hình chóp tam giác đều có 6 cạnh, trong đó 3 cạnh thuộc đáy và 3 cạnh nối từ đỉnh chóp tới các đỉnh của đáy. Hình tứ diện đều có 6 cạnh, tất cả đều bằng nhau.

– Số đỉnh: Hình chóp tam giác đều có 4 đỉnh, trong đó 1 đỉnh là đỉnh chóp và 3 đỉnh thuộc đáy. Hình tứ diện đều cũng có 4 đỉnh, tất cả nằm trên các mặt của hình.

– Độ dài các cạnh: Hình chóp tam giác đều có các cạnh thuộc đáy bằng nhau, nhưng các cạnh nối từ đỉnh chóp tới các đỉnh của đáy không nhất thiết bằng nhau. Hình tứ diện đều có tất cả các cạnh bằng nhau.

– Góc giữa các mặt: Hình chóp tam giác đều có góc giữa hai mặt bên bất kỳ bằng nhau, nhưng góc giữa một mặt bên và mặt đáy không nhất thiết bằng nhau. Hình tứ diện đều có góc giữa hai mặt bất kỳ bằng nhau và bằng 70.53°.

3. Cách vẽ hình chóp tam giác đều:

Để vẽ hình chóp tam giác đều, bạn cần thực hiện các bước sau:

– Bước 1: Vẽ một tam giác đều ABC có cạnh bằng a. Đây là đáy của hình chóp.

– Bước 2: Chọn một điểm M bất kỳ trên đường thẳng vuông góc với mặt phẳng ABC và cách xa mặt phẳng đó một khoảng h. Đây là đỉnh của hình chóp.

– Bước 3: Nối M với các đỉnh A, B, C của tam giác đều để tạo thành các cạnh MA, MB, MC của hình chóp.

– Bước 4: Vẽ các đường chéo AC, MB của tam giác ABC và hình chóp MABC. Điểm O là trung điểm của AC, điểm N là trung điểm của MB. Đường thẳng ON là trục đối xứng của hình chóp.

– Bước 5: Vẽ các đường cao MH, AH, BH, CH của hình chóp. Điểm H là trung điểm của MH. Đường thẳng OH là đường cao của tam giác ONH.

4. Bài tập về hình chóp tam giác đều:

Bài 1: Cho hình chóp tam giác đều SABC cạnh đáy bằng a và cạnh bên bằng 2a. Chứng minh rằng chân đường cao kẻ từ S của hình chóp là tâm của tam giác đều ABC. Tính thể tích chóp đều SABC.

Lời giải:

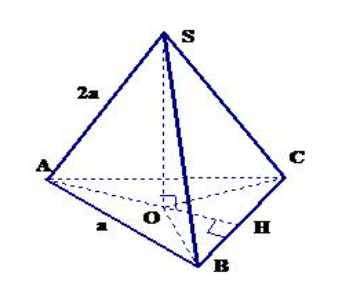
Bước 1: Gọi O là chân đường cao kẻ từ S xuống mặt phẳng (ABC). Vì SABC là hình chóp tam giác đều, nên SO vuông góc với mặt phẳng (ABC) và SA = SB = SC = 2a.

Bước 2: Chứng minh rằng O là tâm của tam giác đều ABC. Ta có thể dùng hai cách:

– Cách 1: Dùng định lí Pythagoras trong các tam giác vuông SOB, SOA và SOC. Ta có:

SO^2 + OB^2 = SB^2

SO^2 + OA^2 = SA^2

SO^2 + OC^2 = SC^2

Do SA = SB = SC = 2a, nên ta suy ra được OB = OA = OC. Do đó, O là trung điểm của BA, BC và AC. Vậy O là tâm của tam giác đều ABC.

– Cách 2: Dùng tính chất của tam giác đều. Ta có:

∠BAS = ∠CAS = ∠SAC (cùng bằng 60 độ)

∠BSA = ∠CSA = ∠SBA (cùng bằng 60 độ)

∠BSC = ∠CSC = ∠SBC (cùng bằng 60 độ)

Do đó, tam giác SAB, SAC và SBC đều là các tam giác đều có cạnh bằng 2a. Khi đó, O là trực tâm của các tam giác này. Vậy O cũng là trực tâm của tam giác ABC. Do tam giác ABC cũng là tam giác đều, nên O là tâm của tam giác ABC.

Bước 3: Tính thể tích chóp SABC. Ta có công thức thể tích hình chóp như sau:

V = (1/3).S.h

Trong đó, S là diện tích đáy, h là chiều cao. Trong trường hợp này, S là diện tích tam giác đều ABC có cạnh bằng a, h là chiều cao SO của hình chóp.

Ta có công thức diện tích tam giác đều như sau:

S = A2 X (√3)/4

Ta cũng có công thức tính chiều cao SO của hình chóp như sau:

SO^2 + (a/2)^2 = (2a)^2

Từ đó, ta suy ra được:

SO = √3.a

Thay vào công thức thể tích hình chóp, ta được:

V = (1/3).(√3/4).a^2.√3.a

V = (√3/4).a^3

Bài 2: Cho hình chóp tứ giác đều O.DEGH có cạnh bên OD = 10 cm và cạnh đáy DE = 7 cm. Hãy cho biết:

a) Mặt bên, mặt đáy và đường cao của hình đó. Mặt đáy và các mặt bên của hình chóp là hình gì?

b) Độ dài các cạnh bên và cạnh đáy còn lại của hình đó

c) Số đo mỗi góc của mặt đáy.

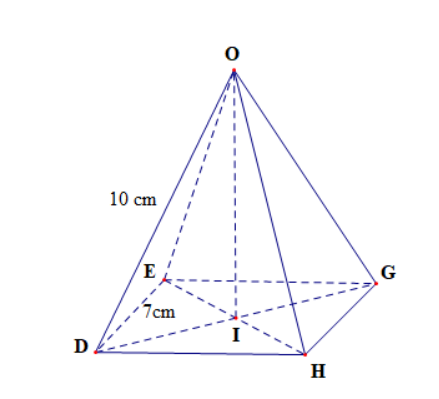
 Lời giải:

a) Hình chóp tứ giác đều O.DEGH có 4 mặt bên là ODE, OEG, OGH, OHD; mặt đáy là DEGH.

Gọi I là giao điểm của hai đường chéo của mặt đáy.

Khi đó OI là đường cao của hình chóp tứ giác đều O.DEGH.

b) Vì bốn mặt bên ODE, OEG, OGH, OHD là các tam giác cân bằng nhau nên OD = OE = OG = OH.

Mà OD = 10 cm, suy ra OE = OG = OH = 10 cm.

Vì mặt đáy DEGH là hình vuông nên DE = EG = GH = HD

Mà DE = 7 cm, suy ra EG = GH = HD = 7 cm.

c) Vì mặt đáy DEGH là hình vuông nên