Góc giữa hai mặt phẳng là góc được hình thành bởi hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó. Cùng bài viết dưới đây tìm hiểu góc giữa hai mặt phẳng là gì? Cách xác định và một số bài tập vận dụng nhé:
Mục lục bài viết
1. Góc giữa hai mặt phẳng là gì?
Khái niệm: Góc giữa hai mặt phẳng là góc được hình thành bởi hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Trong không gian, góc giữa hai mặt phẳng là phần không gian bị chặn giữa hai mặt phẳng đó. Góc giữa hai mặt phẳng được đo bằng góc giữa hai đường thẳng trên mặt hai mặt phẳng đó mà có cùng phương vuông góc với giao tuyến của hai mặt phẳng.
Tính chất: Từ định nghĩa trên, ta có các tính chất sau:
– Góc giữa hai mặt phẳng song song bằng 0 độ.
– Góc giữa hai mặt phẳng trùng nhau bằng 0 độ.
2. Cách xác định góc giữa 2 mặt phẳng:
Để xác định chính xác góc giữa hai mặt phẳng, bạn có thể áp dụng những cách sau đây:
Đặt (P) là mặt phẳng thứ nhất và (Q) là mặt phẳng thứ hai.
– Trường hợp 1: Hai mặt phẳng (P) và (Q) song song hoặc trùng nhau, trong trường hợp này góc giữa hai mặt phẳng được xem là bằng 0.
– Trường hợp 2: Hai mặt phẳng (P) và (Q) không song song hoặc trùng nhau.
– Cách thứ nhất: dựng hai đường thẳng a và b thuộc (P), (Q) và lần lượt vuông góc với hai mặt phẳng đó. Khi đó, ta có góc giữa hai mặt phẳng (P) và (Q) sẽ bằng góc giữa hai đường thẳng a và b.
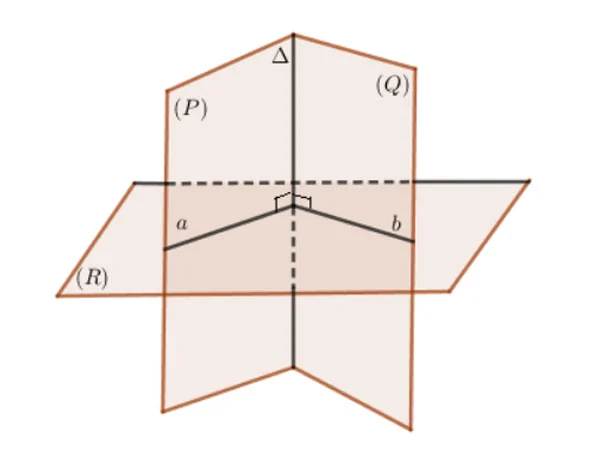
– Cách thứ hai: xác định giao tuyến Δ của hai mặt phẳng (P) và (Q). Sau đó, tìm một mặt phẳng (R) vuông góc với giao tuyến Δ và giao với hai mặt phẳng (P), (R) tại các đường giao a và b.
⇒ Góc giữa hai mặt phẳng (P) và (Q) sẽ là góc giữa hai đường a và b.
3. Bài tập áp dụng
Câu 1: Cho tam giác ABC vuông tại A. Cạnh AB = a nằm trong mặt phẳng(P), cạnh AC = a√2 , AC tạo với (P) một góc 60°. Chọn khẳng định đúng trong các khẳng định sau?
A. (ABC) tạo với (P) góc 45°
B. BC tạo với (P) góc 30°
C. BC tạo với (P) góc 45°
D. BC tạo với (P) góc 60°
Lời giải:
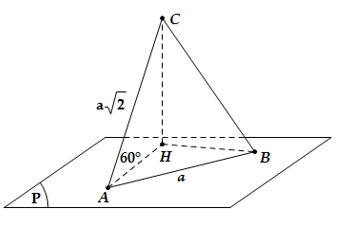
Đáp án C
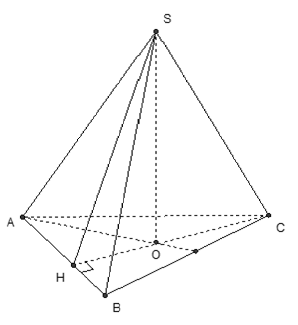
Câu 2: Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai ?
A. Góc giữa hai mặt phẳng (ACD) và (BCD) là góc ∠AIB
B. (BCD) ⊥ (AIB)
C. Góc giữa hai mặt phẳng (ABC) và (ABD) là góc ∠CBD
D. (ACD) ⊥ (AIB)
Lời giải:
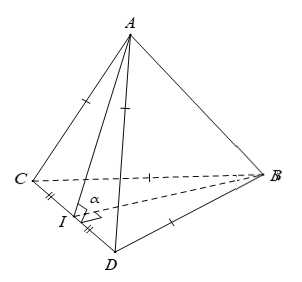
Đáp án C
Câu 3: Cho hình chóp S. ABC có SA ⊥ (ABC) và AB ⊥ BC , gọi I là trung điểm BC. Góc giữa hai mặt phẳng (SBC) và (ABC) là góc nào sau đây?
A. Góc SBA. B. Góc SCA. C. Góc SCB. D. Góc SIA.
Lời giải:
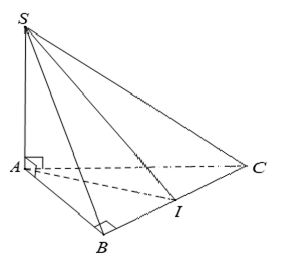
Đáp án A
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA ⊥ (ABCD), gọi O là tâm hình vuông ABCD. Khẳng định nào sau đây sai?
A. Góc giữa hai mặt phẳng (SBC) và (ABCD) là góc ∠ABS
B. Góc giữa hai mặt phẳng (SBD) và (ABCD) là góc ∠SOA
C. Góc giữa hai mặt phẳng (SAD) và (ABCD) là góc ∠SDA
D. (SAC) ⊥ (SBD)
Lời giải:
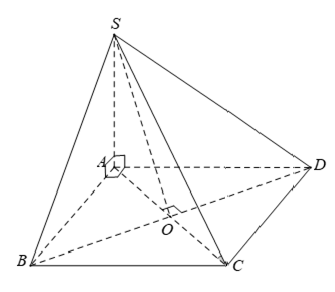
Đáp án C
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Biết SO ⊥ (ABCD), SO = a√3 và đường tròn ngoại tiếp ABCD có bán kính bằng a. Gọi α là góc hợp bởi mặt bên (SCD) với đáy. Khi đó tanα = ?

Lời giải:
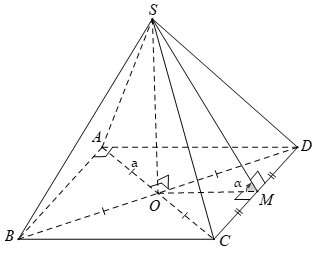
Đáp án D
Câu 6: Cho hình chóp tam giác đều S.ABC với SA = 2AB. Góc giữa (SAB) và (ABC) bằng α. Chọn khẳng định đúng trong các khẳng định sau?
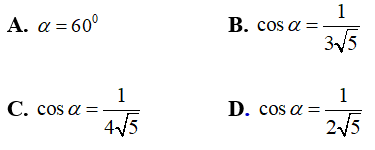
Lời giải:
Đáp án B
Câu 7: Trong không gian cho tam giác đều SAB và hình vuông ABCD cạnh a nằm trên hai mặt phẳng vuông góc. Gọi H; K lần lượt là trung điểm của AB, CD. Ta có tan của góc tạo bởi hai mặt phẳng (SAB) và (SCD) bằng :
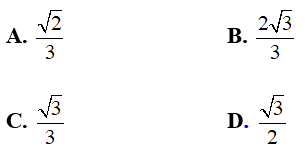
Lời giải:
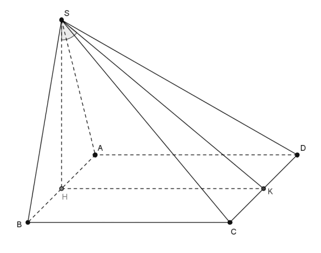
Đáp án B
Câu 8: Cho hình lập phương ABCD.A1B1C1D1 . Gọi α là góc giữa hai mặt phẳng (A1D1CB) và (ABCD). Chọn khẳng định đúng trong các khẳng định sau?
A. α = 45° B. α = 30° C. α = 60° D. α = 90°
Lời giải:
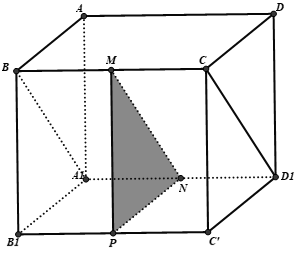
Đáp án A
Câu 9: Cho hình chóp S.ABCD có đáy ABCD là hình vuông có tâm O và SA ⊥ (ABCD). Khẳng định nào sau đây sai ?
A. Góc giữa hai mặt phẳng (SBC) và (ABCD) là góc ∠ABS
B. (SAC) ⊥ (SBD)
C. Góc giữa hai mặt phẳng (SBD) và (ABCD) là góc ∠SOA
D. Góc giữa hai mặt phẳng (SAD) và (ABCD) là góc ∠SDA
Lời giải:
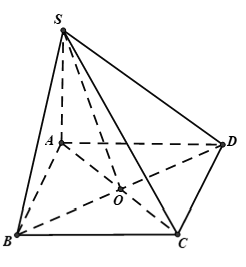
Đáp án D
Câu 10: Cho tứ diện đều ABCD . Tính của góc giữa hai mặt (ABC) và (ACD) .

Lời giải:
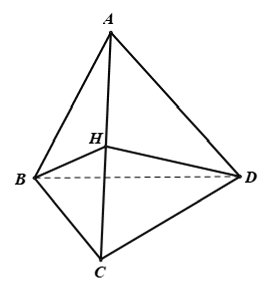
Đáp án A
Câu 11: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc ∠ABC = 60°. Các cạnh SA ; SB ; SC đều bằng a(√3/2) . Gọi φ là góc của hai mặt phẳng (SAC) và (ABCD) . Giá trị tanφ bằng bao nhiêu?
A. 2√5 B. 3√5 C. 5√3 D. Đáp án khác
Lời giải:
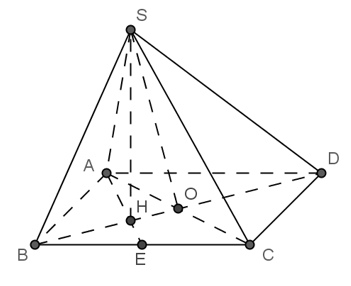
Đáp án D
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D. AB = 2a; AD = DC = a. Cạnh bên SA vuông góc với đáy và SA = a√2. Chọn khẳng định sai trong các khẳng định sau?
A. (SBC) ⊥ (SAC)
B. Giao tuyến của (SAB) và (SCD) song song với AB
C. (SDC) tạo với (BCD) một góc 60°
D. (SBC) tạo với đáy một góc 45°
Lời giải:
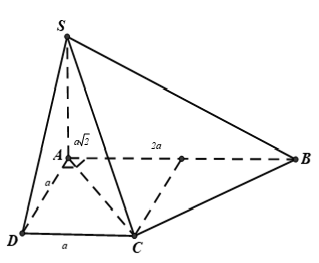
Đáp án C
Câu 13: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = AA’ = a; AD = 2a. Gọi α là góc giữa đường chéo A’C và đáy ABCD. Tính α .
A. α ≈ 20°45′ B. α ≈ 24°5′ C. α ≈ 30°18′ D. α ≈ 25°48′
Lời giải:
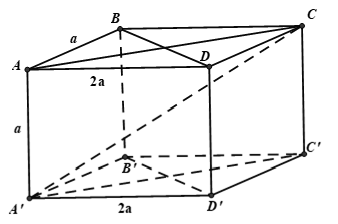
Chọn B.
Từ giả thiết ta suy ra: AA’ ⊥ (ABCD) nên AC là hình chiếu vuông góc của A’C lên mặt phẳng (ABCD)
⇒ (A’C, (ABCD)) = (A’C, AC) = ∠A’CA = α
Áp dụng định lý Pytago trong tam giác ABC vuông tại B ta có:
AC2 = AB2 + BC2 = a2 + 4a2 = 5a2 ⇒ AC = a√5 .
Áp dụng hệ thức lượng trong tam giác AA’C vuông tại A ta có:
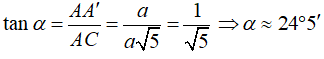
Câu 14: Cho hình lập phương ABCD.A’B’C’D’. Xét mặt phẳng (A’BD). Trong các mệnh đề sau mệnh đề nào đúng?
A. Góc giữa mặt phẳng ( A’BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng α mà tanα = 1/√2 .
C. Góc giữa mặt phẳng (A’BD) và các mặt phẳng chứa các cạnh của hình lập phương phụ thuộc vào kích thước của hình lập phương.
D. Góc giữa mặt phẳng ( A’BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng nhau.
Lời giải:
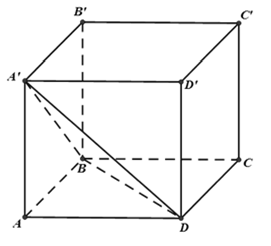
ABCD.A’B’C’D’ là hình lặp phương nên hình chiếu của tam giác A’BD lên các mặt chứa các cạnh của hình lặp phương là các tam giác bằng nhau.
Gọi S1 là diện tích các tam giác này
Lại có S1 = SAD’B.cosα
⇒ Góc giữa mặt phẳng (A’BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng nhau.
Vậy chọn đáp án D
Câu 15: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi cạnh bên và mặt đáy.
A. 30° B. 45° C. 60° D. 75°
Lời giải:
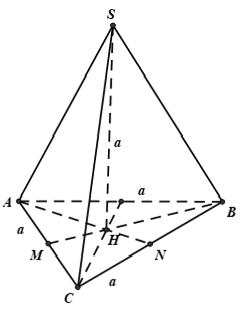
Đáp án C




