Trong không gian Oxyz, mặt phẳng (Oxy) có phương trình là dạng toán quen thuộc đối với các bạn học sinh. Bài viết dưới đây cung cấp thông tin về Trong không gian Oxyz, mặt phẳng (Oxy) có phương trình, mời các bạn cùng tham khảo.
Mục lục bài viết
1. Trong không gian Oxyz, mặt phẳng (Oxy) có phương trình là:
A. z = 0
B. x + y + z
C. y = 0
D. x = 0
Đáp án đúng là đáp án A
Mặt phẳng (Oxy) đi qua O, véc-tơ pháp tuyến ![]() có phương trình 1(z – 0) = 0 <=> z = 0.
có phương trình 1(z – 0) = 0 <=> z = 0.
2. Phương trình mặt phẳng trong không gian:
– Vectơ pháp tuyến của mặt phẳng.
* Cho mặt phẳng (P), vectơ → n ≠ → 0 mà giá của nó vuông góc với mặt phẳng ( P ) thì → n được gọi là vectơ pháp tuyến của mặt phẳng ( P ) .
* Cho mặt phẳng ( P ), cặp vectơ → a ≠ → 0, → b ≠ → 0 không cùng phương mà giá của chúng là hai đường thẳng song song hay nằm trong mặt phẳng (P) được gọi là cặp vectơ chỉ phương của mặt phẳng (P). Khi đó vectơ → n = [ → a . → b ] là vectơ pháp tuyến của mặt phẳng ( P ).
* Nếu → a = ( a 1 ; a 2 ; a 3 ), → b = ( b 1 ; b 2 ; b 3 ) thì:
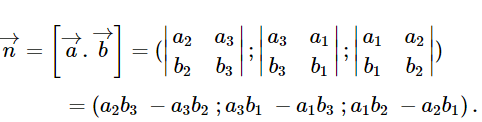
* Mặt phẳng hoàn toàn được xác định khi biết một điểm và một vectơ pháp tuyến của nó, hay một điểm thuộc mặt phẳng và cặp vectơ chỉ phương của nó.
– Phương trình mặt phẳng.
* Mặt phẳng (P) qua điểm M0 (x0; y0; z0) và nhận → n (A, B, C) làm vectơ pháp tuyến có phương trình có dạng: A(x – x0) + B(y – y0) + C(z – z0)
* Mọi mặt phẳng trong không gian có phương trình tổng quát có dạng: Ax + By + Cz + D = 0 ở đó A2 + B2 + C2 > 0.
Khi đó vectơ ->n(A; B; C) là vectơ pháp tuyến của mặt phẳng.
* Mặt phẳng đi qua ba điểm M(a; 0; 0), N(0; b; 0), C(0; 0; c) ở đó abc ≠ 0 có phương trình: x/ a+ y/ b + z/ c = 1. Phương trình này còn được gọi là phương trình mặt phẳng theo đoạn chắn.
– Vị trí tương đối của hai mặt phẳng.
Cho hai mặt phẳng (P1) và (P2) có phương trình:
(P1): A1x + B1y + C1z + D1 = 0:
(P2) : A2x + B2y + C2z + D2 = 0.
Ta có → n 1 (A 1; B1; C1) ⊥ (P1) và → n2 (A2 ; B2 ; C2 ) ⊥ (P2). Khi đó:
(P1) ⊥ (P2) ⇔ → n1 ⊥ ->n2 ⇔ ->n1 . → n2 <=> A1A2 + B1B2 + C1C2
(P1) / / (P2) ⇔ → n1 = k . → n1 và D1 ≠ k . D2 ( k ≠ 0 ).
(P1) ≡ (P2) ⇔ → n1 = k . → n2 và D1 = k . D2.
(P1) cắt (P2) ⇔ → n1 ≠ k . → n2 (nghĩa là n1 và → n1 không cùng phương).
– Khoảng cách từ một điểm đến một mặt phẳng.
Trong không gian Oxyz cho mặt phẳng (P) có phương trình: Ax +Bx +Cz + D = 0 và điểm M0 x0 ; y0 ; z0). Khoảng cách từ M0 đến (P) được cho bởi công thức:
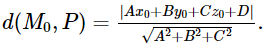
– Góc giữa hai mặt phẳng.
Cho hai mặt phẳng (P1) và (P2) có phương trình:
(P1) : A1x + B1y+ C1z + D1 = 0;
(P2): A2x + B2y + C2z + D2 = 0. Gọi φ là góc giữa hai mặt phẳng (P1) và (P2) thì 0 ≤ φ ≤ 900 và:
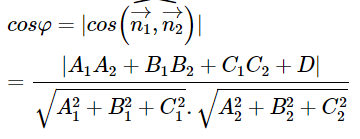
3. Bài tập ôn luyện về phương trình mặt phẳng:
Dạng 1: Xác định vectơ pháp tuyến của mặt phẳng Phương pháp giải: Cho mặt phẳng (α) có phương trình Ax + By + Cz + D = 0. Khi đó mặt phẳng (α) có một VTPT là → n = ( A; B; C).
Bài tập: Trong không gian Oxyz, cho mặt phẳng (P): 2x – 4y + 5 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (P)?
A. → n2 = (2; 4; 0)
B. → n1 = (-1; 2; 0)
C. → n3 = (0; 2; 4)
D. → n 4 = (2; -4; 5)
Hướng dẫn giải:
Ta có (P): 2x – 4y + 5 = 0 có một vectơ pháp tuyến là → n = (2; – 4; 0) = -1/ 2 (-1; 2; 0).
Vậy một vectơ pháp tuyến của mặt phẳng (P) là → n1 = (-1; 2; 0).
Chọn B.
Dạng 2: Viết phương trình mặt phẳng khi đã biết một điểm đi qua và vectơ pháp tuyến
Phương pháp giải:
Cho mặt phẳng (α) đi qua điểm M0(x0; y0; z0) và nhận vectơ → n = (A; B; C) làm vectơ pháp tuyến. Khi đó phương trình mặt phẳng (α) là
A(x – x0) + B(y – y0) + C(z – z0) = 0
Bài tập: Trong không gian Oxyz, mặt phẳng đi qua điểm A (2; 0; -2) và nhận → n = ( 1 ; 2 ; 3 ) làm véc tơ pháp tuyến có phương trình là:
A. x + 2y + 3z + 4 = 0.
B. x + 2y + 3z – 8 = 0.
C. x – z + 2 = 0.
D. x – z – 4 = 0.
Hướng dẫn giải:
Phương trình mặt phẳng cần tìm là:
1(x – 2) + 2(y – 0) + 3[z – (-2)] = 0
⇔ x + 2y + 3z + 4 = 0.
Chọn A.
Dạng 3: Viết phương trình mặt phẳng (α) đi qua điểm M và song song với mặt phẳng (P) cho trước. Phương pháp giải:
+) Mặt phẳng (α) song song với mặt phẳng (P) cho trước nên vectơ pháp tuyến của mặt phẳng (α) chính là vectơ pháp tuyến của mặt phẳng (P).
+) Từ đó viết phương trình mặt phẳng (α) đi qua M và có vectơ pháp tuyến là:
→ n (α) = → n (P).
Bài tập:Trong không gian Oxyz, mặt phẳng (Q) đi qua điểm A (1; 2; -1) và song song với (α): 3x + 4y – z + 1 = 0 có phương trình là:
A. 3 x + 4 y − z − 12 = 0
B. 3 x + 4 y − z + 10 = 0
C. 3 x + 4 y − z − 10 = 0
D. 3 x + 4 y − z + 12 = 0
Hướng dẫn giải:
(α) có một vectơ pháp tuyến là → n (α) = (3; 4; -1).
Do ( Q ) // ( α ) ⇒ → n (Q) = (3; 4; -1).
Vì (Q) đi qua A (1; 2; -1) nên phương trình mặt phẳng (Q) là:
3(x – 1) + 4(y – 2) – 1(z + 1) = 0
⇔ 3x + 4y – z – 12 = 0
Chọn A.
Dạng 4: Viết phương trình mặt phẳng (α) đi qua điểm M và vuông góc với hai mặt phẳng (P) và (Q).
Phương pháp giải: Gọi → n (α) , → n (P), → n (Q) lần lượt là vectơ pháp tuyến của mặt phẳng (α), (P), (Q). Vì mặt phẳng (α) vuông góc với hai mặt phẳng (P) và (Q) nên ta có:
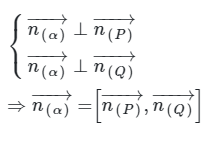
Từ đó viết phương trình mặt phẳng (α) đi qua M và có vectơ pháp tuyến là → n (α) đã tính phía trên.
Bài tập: Cho hai mặt phẳng (P): 3x – 2y + 2z + 7 = 0 và (Q): 5x – 4y + 3z + 1 = 0. Gọi (R) là mặt phẳng đi qua gốc toạ độ O và vuông góc với cả (P) và (Q). Khi đó phương trình mặt phẳng (R) là:
A. 2x – y + 2z = 0
B. 2x + y – 2z = 0
C. 2x + y – 2z + 1 = 0
D. 2x – y – 2z = 0.
Hướng dẫn giải: Gọi → n1, → n2, → n3 lần lượt là véctơ pháp tuyến của (P), (Q), (R).
Theo bài ra ta có:
→ n1 = (3; -2; 2), → n2 = (5; -4; 3).
Vì mặt phẳng (R) vuông góc với cả (P) và (Q) nên ta có:
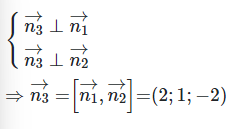
Vì (R) là mặt phẳng đi qua gốc toạ độ O (0; 0; 0) nên ta có phương trình mặt phẳng (R) là:
2(x – 0) + 1(y – 0) – 2(z – 0) = 0
⇔ 2x + y – 2z = 0
Chọn B.
Dạng 5: Viết phương trình mặt phẳng ( α ) đi qua hai điểm A, B và vuông góc với mặt phẳng (P).
Phương pháp giải: Gọi → n (α), → n (P) lần lượt là vectơ pháp tuyến của mặt phẳng (α) và mặt phẳng (P). Vì mặt phẳng ( α ) đi qua A, B và vuông góc với mặt phẳng (P) nên ta có:
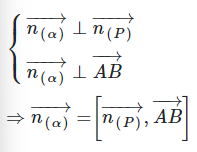
Từ đó viết phương trình mặt phẳng (α) đi qua A (hoặc B) và có vectơ pháp tuyến là → n (α) đã tính phía trên
Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M (-1; 2; 0) và song song với mặt phẳng (Q): x + 2y – 3z + 10 = 0.
A. x + 2y – 3z – 3= 0 B. x – 2y+ 3z + 5 = 0
C. x+ 2y – 3z +3 = 0 D. – x+ 2y + 10 = 0
Hướng dẫn giải:
Mặt phẳng (P) song song với mặt phẳng (Q) nên vecto pháp tuyến của mặt phẳng (P) là n→(1;2-3) .
Mặt phẳng (P) đi qua điểm M ( -1; 2; 0) và có vecto pháp tuyến n→(1;2-3) nên có phương trình:
1( x+1) + 2(y- 2) – 3( z- 0) = 0 hay x+ 2y – 3z – 3 = 0
Chọn A.




