Tìm tỉ số đồng dạng của hai tam giác là một kiến thức quan trọng trong phần Toán hình học lớp 8 và có ứng dụng rộng rãi sau này. Cùng bài viết này tìm hiểu lý thuyết, phương pháp giải và một số bài tập tự luyện dạng toán này nhé:
Mục lục bài viết
1. Phương pháp giải dạng tìm tỉ số đồng dạng của hai tam giác:
+) Khái niệm:
Hai tam giác được coi là đồng dạng với nhau nếu chúng có ba cặp góc bằng nhau và ba cặp cạnh tương ứng tỉ lệ.
Phép đồng dạng có kí hiệu là: ∼
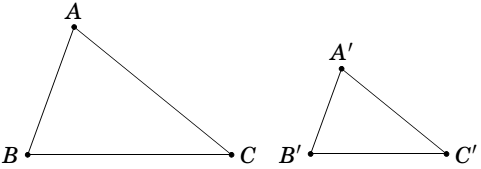ΔA’B’C’ gọi là đồng dạng với ΔABC nếu
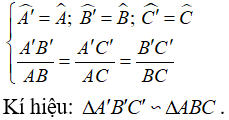
* Tỉ số các cạnh tương ứng 
được gọi là tỉ số đồng dạng của hai tam giác.
+) Tính chất:
– Mỗi tam giác đồng dạng với chính nó.
– Tính chất giao hoán: Nếu tam giác ABC đồng dạng với tam giác A’B’C’ thì ngược lại, tam giác A’B’C’ cũng đồng dạng với tam giác ABC
– Tính chất bắc cầu: Nếu tam giác ABC đồng dạng với tam giác DEF. Mà tam giác DEF lại đồng dạng với tam giác HIK thì ta có thể suy ra rằng: Tam giác ABC đồng dạng với tam giác HIK.
Mô tả:
Ngoài ra, hai tam giác đồng dạng còn có các tính chất như:
– Tỉ số diện tích của hai tam giác đồng dạng chính bằng bình phương của tỉ số đồng dạng.
– Tỉ số hai đường cao tương ứng bằng với tỷ số đồng dạng
– Tỉ số hai đường trung tuyến (Đường xuất phát từ một góc đi qua trung điểm của cạnh đối diện) cũng bằng tỷ số đồng dạng
– Tỉ số chu vi của hai tam giác bằng với tỷ số đồng dạng.
Nếu bạn chưa rõ tỷ số đồng dạng là gì thì nó chính là tỷ số của hai cặp cạnh trong tam giác đồng dạng đó. Ví dụ:
Ta có hai tam giác ABC và tam giác A’B’C’ (Như hình vẽ) là tam giác đồng dạng. Tỷ số đồng dạng của chúng sẽ là:
A’B’/AB = B’C’/BC = 1/2 (= 2/4 = 3/6).
Như vậy, tỉ lệ diện tích S∆A’B’C’/ S∆ABC =(1/2)^2=1/4.
Bạn lưu ý: Đường trung trực (Đường vuông góc tại trung điểm của một đoạn thẳng) không liên quan gì tới tam giác đồng dạng đâu nhé.
+) Định lí:
Ta có định lý Ta-lét như sau: Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
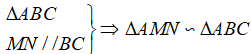
Bên cạnh đó, ta cũng có định lý Ta-lét đảo như sau: Nếu một đường thẳng cắt hai cạnh của tam giác tại hai điểm và nó tạo ra những đoạn thẳng tương ứng tỉ lệ trên hai cạnh này thì đường thẳng đó song song với cạnh còn lại của tam giác.
Hệ quả: Định lý cũng đúng cho trường hợp đường thẳng cắt phần kéo dài hai cạnh của tam giác và song song với cạnh còn lại.
+) Các trường hợp đồng dạng của tam giác:
Ở mỗi loại tam giác thường và tam giác vuông, chúng ta đều có tất cả 3 trường hợp tam giác đồng dạng như sau:
– Trường hợp đồng dạng trong tam giác thường
*Trường hợp đồng dạng 1: Cạnh – cạnh – cạnh
Nếu hai tam giác có ba cặp cạnh tương ứng bằng nhau thì hai tam giác đó được coi là đồng dạng với nhau. Ví dụ được biểu diễn minh họa qua hình vẽ:
Chứng minh: – Xét hai tam giác ABC và tam giác A’B’C’, ta có:
AB=A’B’=5cm
BC=B’C’=6cm
AC=A’C’=4cm
-> ∆ABC ∼ ∆A’B’C’ (dpcm – Điều phải chứng minh)
*Trường hợp đồng dạng 2: Góc – góc
Nếu hai tam giác có một trong hai cặp góc tương ứng bằng nhau thì được gọi là đồng dạng với nhau.
Chứng minh: Xét hai tam giác ABC và tam giác A’B’C’, ta có:
Góc A = Góc A’
Góc B = Góc B’
> ∆ABC ∼ ∆A’B’C’ (dpcm)
*Trường hợp đồng dạng 3: Góc – cạnh – góc
Nếu hai tam giác có hai cặp cạnh tương ứng tỉ lệ với nhau và một góc xen giữa hai cặp cạnh đó bằng nhau thì chúng được gọi là hai tam giác đồng dạng.
Chứng minh: Xét hai tam giác ABC và tam giác A’B’C’, ta có:
AB/A’B’ = AC/A’C’
Góc A = Góc A’
-> ∆ABC ∼ ∆A’B’C’ (dpcm)
– Trường hợp đồng dạng trong tam giác vuông:
*Trường hợp đồng dạng 1: Cạnh huyền – cạnh góc vuông
Nếu tam giác vuông này có cặp cạnh huyền và cạnh góc vuông tỷ lệ với cạnh huyền và cạnh góc vuông của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Chứng minh: Xét hai tam giác vuông ABC và tam giác A’B’C’, ta có:
AB/A’B’= BC/B’C’
Góc A = Góc A’ = 90 độ
-> ∆ABC ∼ ∆A’B’C’ (dpcm)
*Trường hợp đồng dạng 2: Hai cặp cạnh góc vuông
Nếu hai tam giác vuông có hai cặp cạnh góc vuông tỷ lệ với nhau thì hai tam giác đó được gọi là đồng dạng với nhau.
Chứng minh: Xét hai tam giác vuông ABC và tam giác A’B’C’, ta có:
AB/A’B’= AC/A’C’
Góc A = Góc A’ = 90 độ
-> ∆ABC ∼ ∆A’B’C’ (dpcm)
*Trường hợp đồng dạng thứ 3: Góc – góc
Nếu hai tam giác vuông có hai góc nhọn bằng nhau thì hai tam giác đó đồng dạng với nhau.
Điều này cũng khá dễ hiểu vì hai tam giác vuông này vốn dĩ đã có hai góc vuông bằng nhau trước đó rồi.
Chứng minh: Xét hai tam giác vuông ABC và tam giác A’B’C’, ta có:
Góc B = Góc B’
Góc A = Góc A’ = 90 độ
-> ∆ABC ∼ ∆A’B’C’ (dpcm)
2. Ví dụ minh họa:
Câu 1: Cho tam giác ABC đồng dạng với tam giác A’B’C’. Hãy chọn phát biểu sai:
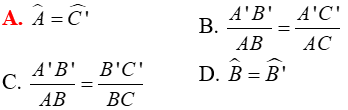
Lời giải:.
Dựa vào định nghĩa hai tam giác đồng dạng:
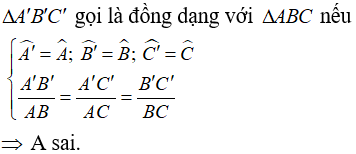
Câu 2: Nếu tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số k thì tỉ số chu vi của hai tam giác đó bằng:
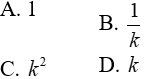
Lời giải:
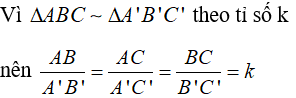
Ta có:
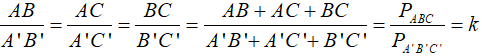
Câu 3: Cho tam giác ABC đồng dạng với tam giác MNP theo tỉ số 2/3, biết chu vi của tam giác ABC bằng 40cm. Tính chu vi của tam giác MNP?
Lời giải:
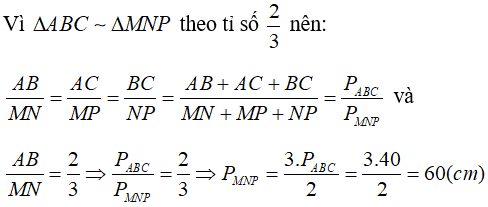
Vậy chu vi của tam giác MNP là 60cm.
Câu 4: Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD và ΔBCD.
a) Chứng minh ABCD là hình thang
b) Cho AB = 2cm, AD = 3cm, CD = 8cm. Tính độ dài BD, BC?
Lời giải:
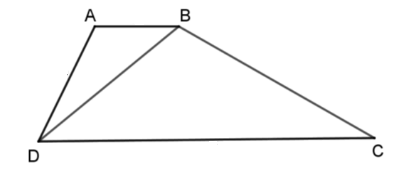
Vậy BD = 4cm, BC = 6cm.
3. Bài tập tự luyện:
Câu 1: Cho hình vẽ sau biết MN // AB. Khẳng định nào sau đây là sai?
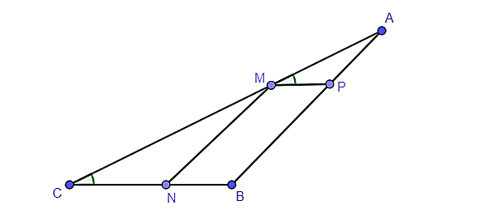
A. ΔAMP ᔕ ΔACB;
B. ΔMCN ᔕ ΔACB;
C. ΔAMP ᔕ ΔMCN;
D. Cả A, B, C đều sai.
Xét tam giác ABC, do MN // AB nên ΔMCN ᔕ ΔACB.
Lại có AMP^ = ACB^”>AMP^ = ACB^ mà hai góc này ở vị trí đồng vị nên MP // CB.
Xét tam giác ABC, do MP // CB nên ΔAMP ᔕ ΔACB.
Vì ΔMCN ᔕ ΔACB, ΔAMP ᔕ ΔACB nên ΔAMP ᔕ ΔMCN.
Vậy D sai.
Câu 2: Cho hình bình hành ABCD. Lấy E trên cạnh BC, tia DE cắt AB tại F. Khi đó tam giác FBE đồng dạng với tam giác nào dưới đây?
A. Tam giác FAD;
B. Tam giác DCE;
C. Cả A, B đều sai;
D. Cả A, B đều đúng.
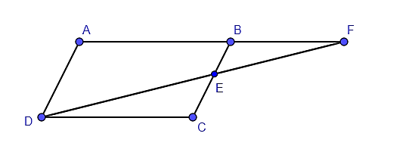
Vì ABCD là hình bình hành nên AB // CD và AD // BC.
Xét tam giác FAD, do BE // AD (E ∈ BC, AD // BC) nên ΔFBE ᔕ ΔFAD.
Xét tam giác DEC, do BF // DC (AB // CD) nên ΔFBE ᔕ ΔDCE.
Vậy ΔFBE ᔕ ΔFAD và ΔFBE ᔕ ΔDCE.
Câu 3: Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Trong hình vẽ được có bao nhiêu cặp tam giác đồng dạng?
A. 4;
B. 6;
C. 8;
D. 10.
Đáp án: D
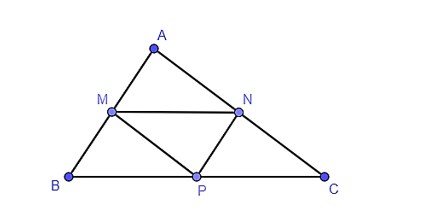
Vì M, N lần lượt là trung điểm của AB, AC.
Suy ra MN là đường trung bình của tam giác ABC nên MN // BC.
Vì M, P lần lượt là trung điểm của AB, BC.
Suy ra MP là đường trung bình của tam giác ABC nên MP // AC.
Vì N, P lần lượt là trung điểm của AC, BC.
Suy ra NP là đường trung bình của tam giác ABC nên NP // AB.
Xét tam giác ABC:
+ Do MN // BC nên ΔAMN ᔕ ΔABC.
+ Do MP // AC nên ΔMBP ᔕ ΔABC.
+ Do NP // AB nên ΔNPC ᔕ ΔABC.
Vì ΔAMN ᔕ ΔABC, ΔMBP ᔕ ΔABC, ΔNPC ᔕ ΔABC nên các tam giác AMN, MBP, NPC đôi một đồng dạng với nhau.
Xét hai tam giác AMN và PNM có:
AM = PN =12AB”>=12AB
MN: Cạnh chung
MP = AN =12AC”>=12AC
Suy ra ΔAMN = ΔPNM (c – c – c).
Do đó, ΔAMN ᔕ ΔPNM.
Từ đó suy ra 5 tam giác AMN, PNM, MBP, NPC, ABC đôi một đồng dạng với nhau.
Vậy có tất cả 10 cặp tam giác đồng dạng.
Câu 4: Cho hình dưới đây, khi đó độ dài cạnh AC
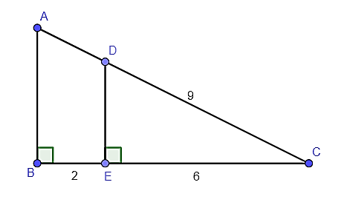
A. 3;
B. 43″>43;
C. 12;
D. 163″>163.
Có BC = CE + EB = 6 + 2 = 8.
Ta có DE ⊥ BC, AB ⊥ BC nên DE // AB.
Xét tam giác ABC, do DE // AB nên ΔCDE ᔕ ΔCAB.
Suy ra CDCA=CECB”>CDCA=CECB hay 9CA=68″>9CA=68.
Suy ra CA=9⋅86=12″>CA=9⋅86=12.
Câu 5: Hãy chọn câu sai
A. Hai tam giác bằng nhau thì đồng dạng
B. Hai tam giác đều luôn đồng dạng với nhau
C. Hai tam giác đồng dạng là hai tam giác có tất cả các cặp góc tương ứng bằng nhau và các cặp cạnh tương ứng tỉ lệ
D. Hai tam giác vuông luôn đồng dạng với nhau
Đáp án: D
+ Hai tam giác đều có các góc đều bằng 600 và các cạnh tương ứng tỉ lệ nên chúng đồng dạng.
+ Hai tam giác vuông chưa chắc đồng dạng nên D sai.
Câu 6: Hình thang ABCD (AB//CD) có AB = 10cm, CD = 25cm, hai đường chéo cắt nhau tại O. Chứng minh 
và tìm tỉ số đồng dạng (nếu có).
Đáp án:
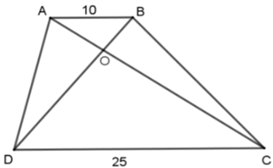
AB // CD nên ΔAOB ⁓ ΔCOD.
Tỉ số đồng dạng AOOC=BOOD=ABCD=1025=25″>
