Nắm rõ được dấu hiệu nhận biết và các tính chất đặc biệt của tam giác đều sẽ giúp các bạn học sinh tự tin nắm vững được kiến thức để giải toán. Bài viết dưới đây cung cấp cho các bạn những kiến thức quan trọng về tam giác đều trong chương trình Toán trung học cơ sở.
Mục lục bài viết
1. Tam giác đều là gì?
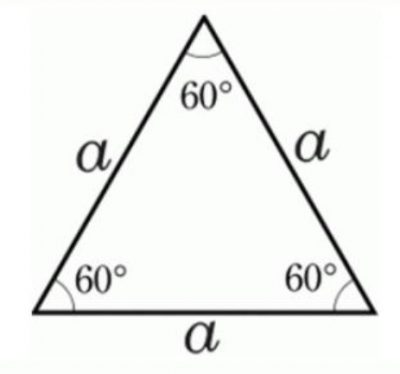
Trong hình học, tam giác đều là tam giác có ba cạnh bằng nhau hoặc tương đương ba góc bằng nhau và bằng 60°. Nó là một đa giác đều với số cạnh bằng 3.
Trong tam giác ABC đều có AB = AC = BC.
Hệ quả:
– Trong một tam giác đều thì mỗi góc bằng 60°
– Nếu một tam giác có 3 góc bằng nhau thì đó là tam giác đều.
– Nếu một tam giác cân có 1 góc bằng 60° thì đó là tam giác đều.
2. Dấu hiệu nhận biết tam giác đều:
– Tam giác có ba cạnh bằng nhau là tam giác đều
– Tam giác có ba góc bằng nhau là tam giác đều
– Tam giác cân có một góc bằng 600 là tam giác đều
– Tam giác có hai góc bằng 600 là tam giác đều
Cách chứng minh tam giác đều:
Cách 1: Chứng minh tam giác đó có 3 cạnh bằng nhau.
Ví dụ: Tam giác OAB có OA = OB = AB
=> Tam giác OAB đều
Cách 2: Chứng minh tam giác đó có 3 góc bằng nhau.
Ví dụ: Chứng minh tam giác OAB có góc O = B = A
=> Tam giác OAB đều
Cách 3: Chứng minh tam giác đó cân và có một góc bằng 60 độ.
Ví dụ: Tam giác OAB có OA = OB và Ô = 60°
=> Tam giác OAB đều
Cách 4: Chứng minh tam giác đó có 2 góc bằng 60 độ.
Ví dụ: Tam giác OAB có góc A = B = 60°
=> Tam giác OAB đều
3. Tính chất tam giác đều:
Trong tam giác đều mỗi góc bằng nhau và bằng 60 độ.
Trong tam giác ABC: góc A = góc B = góc C = 60 độ
Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
Nếu ABC là tam giác đều thì: góc A = góc B = góc C
Nếu một tam giác cân có một góc bằng 60 độ thì tam giác đó là tam giác đều.
Trong tam giác đều, đường trung tuyến của tam giác đồng thời là đường cao và đường phân giác của tam giác đó.
Tam giác ABC đều có AD là đường trung tuyến kẻ từ đỉnh A. Khi đó, AD là đường cao và đường phân giác của tam giác ABC.
Cách dựng tam giác đều:
Cách dựng tam giác đều ABC
– Vẽ cạnh BC
– Vẽ (B; BC) và (C; BC)
– (B; BC) ∩ (C; BC) tại A
ABC là tam giác đều cần vẽ.
Tính chất trọng tâm tam giác:
Tính chất của trọng tâm tam giác là: Khoảng cách từ trọng tâm tới 3 đỉnh của tam giác bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.
Giả sử, tam giác ABC có 3 đường trung tuyến là AM, BN, CP với G là trọng tâm như hình. Theo tính chất trên, ta có:
– GA = 2/3 AM
– GB = 2/3 AN
– GC = 2/3 CP
Xét tam giác đều ABC với G là giao điểm của 3 đường trung tuyến xuất phát từ 3 đỉnh. Khi đó, G vừa là trọng tâm, trực tâm, tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp của tam giác đều ABC.
4. Công thức tính tam giác đều:
4.1. Công thức tính diện tích tam giác đều:
Diện tích tam giác đều bằng 1/2 tích của đáy nhân với chiều cao, công thức như sau:
S = 1/2 (axh)
Trong đó:
S là diện tích của tam giác
a là chiều dài của cạnh cơ sở
h là chiều cao
Ví dụ: Tính diện tích tam giác đều cạnh:
a, Độ dài một cạnh của tam giác là 6cm và chiều cao là 10cm.
b, Độ dài một cạnh của tam giác là 4cm và chiều cao là 5cm.
Câu trả lời:
a, Diện tích của tam giác là: (6 x 10): 2 = 30 (cm.)2)
Đáp số: 30cm2
b, Diện tích hình tam giác là: (4 x 5): 2 = 10 (cm2)
Đáp số: 10 cm2
Những lưu ý khi tính diện tích tam giác:
– Với tam giác có chứa góc bẹt chiều cao nằm bên ngoài tam giác khi đó độ dài cạnh để tính diện tích chính bằng độ dài cạnh trong tam giác.
– Khi tính diện tích tam giác chiều cao nào ứng với đáy đó.
– Nếu hai tam giác có chung chiều cao hoặc chiều cao bằng nhau, suy ra diện tích hai tam giác tỉ lệ với 2 cạnh đáy và ngược lại, nếu hai tam giác có chung đáy (hoặc hai đáy bằng nhau), suy ra diện tích tam giác tỉ lệ với 2 đường cao tương ứng.
4.2. Công thức tính chu vi tam giác đều:
Chu vi hình tam giác đều bằng tổng 3 cạnh của tam giác, công thức:
P = a + a + a hoặc P = 3 xa
Trong đó:
P là chu vi của tam giác
a là cạnh của tam giác
Ví dụ: Tính chu vi tam giác đều ABC có độ dài cạnh AB = 5 cm
Câu trả lời:
=> Vì tam giác ABC là tam giác đều nên ta có, độ dài các cạnh là: AB = AC = BC = 5cm
Dựa vào công thức tính chu vi hình tam giác đều, ta có: P (ABC) = 5 x 3 = 15cm
Bán kính đường tròn nội tiếp tam giác đều:
r = a x √3 / 6
Bán kính đường tròn ngoại tiếp tam giác đều:
R = a x √3 / 3
4.3. Công thức tính đường cao tam giác đều:
Trong tam giác đều đường cao cũng là đường phân giác cũng là đường trung tuyến
Biểu thức: h = a x √3 / 2
Trong đó:
a là độ dài cạnh tam giác đều
h là chiều cao tam giác
5. Ví dụ minh hoạ và bài tập áp dụng:
5.1. Ví dụ minh họa:
Ví dụ 1: Cho ΔABC đều, trên cạnh AB lấy điểm E, trên cạnh AC lấy điểm F, trên cạnh BC lấy điểm P sao cho BE = AF = PC. Chứng minh ΔEFP là tam giác đều.
Tự vẽ hình
Hướng dẫn giải
Ta có:
AB = BC = AC
BE = CP = AF
AB = AE + EB; BC = BP + PC; AC = AF + FC
⇒ AE = BP = FC
Xét 3 tam giác ΔAFE, ΔBEF và ΔCPF có:
AF = BE = CP (giả thiết)
AE = BP = FC
Góc A = Góc B = Góc C (góc của tam giác đều)
⇒ ΔAFE = ΔBEF = ΔCPF
⇒ EF = PE = FP
Do đó ΔEFP là tam giác đều (3 cạnh bằng nhau)
Ví dụ 2: Cho tam giác ABC có góc A = 60 độ. Vẽ AD là phân giác của góc BAC (D ∈ BC). Từ B vẽ BK ⊥ AC (K ∈ BC) và vẽ BH ⊥ AD tại H.
a) Chứng minh Δ AHB = Δ BKA
b) Tia BH cắt AC tại M. Chứng minh tam giác ABM là tam giác đều.
Tự vẽ hình
Hướng dẫn giải:
a) Xét hai tam giác vuông AHB và BKA có:
góc BAH= góc ABK= 30 độ
Cạnh AB chung
Vậy Δ AHB = Δ BKA (cạnh huyền-góc nhọn).
b, Ta có góc ABH = góc BAK (vì Δ AHB = Δ BKA)
Hay góc ABM = góc BAM
Xét tam giác ABM có góc ABM = góc BAM = 60 độ
Nên tam giác ABM là tam giác đều. (đpcm)
Ví dụ 3: Cho tam giác đều ABC. Lấy các điểm D, E, F theo thứ tự thuộc các cạnh AB, BC, CA sao cho AD = BE = CF. Chứng minh rằng ∆DEF là tam giác đều.
Tự vẽ hình
Hướng dẫn giải:
Ta có: AB = AD + DB (1)
BC = BE + EC (2)
AC = AF + FC (3)
AB = AC = BC (giả thiết) (4)
AD = BE = CF (giả thiết) (5)
Từ (1), (2), (3), (4) và (5) suy ra:
BD = EC = AF
Xét ∆ADF và ∆BED, ta có:
AD = BE (giả thiết)
Góc A = góc B = 60 độ ( vì tam giác ABC đều)
AE = BD (chứng minh trên)
Suy ra: ∆ADF = ∆BED (cạnh – góc – cạnh)
Suy ra: DF = DE (hai cạnh tương ứng) (6)
Xét ∆ADF và ∆CFE ta có:
AD = CF (gt)
Góc A = Góc B (vì ∆ABC đều)
EC = AF (chứng minh trên)
Suy ra : ∆ADF = ∆CFE (cạnh – góc – cạnh)
Suy ra: DF = FE (hai cạnh tương ứng) (7)
Từ (6) và (7) suy ra: DF = ED = FE
Vậy ∆DEF đều.
Ví dụ 4: Vẽ tam giác đều ABC có cạnh bằng 4 cm.
Giải:
– Vẽ đoạn thẳng BC = 4 cm
– Vẽ cung tròn tâm B bán kính 4 cm.
– Vẽ cung tròn tâm C bán kính 4 cm.
– Hai cung tròn này cắt nhau tại A.
– Nối AB, AC ta được tam giác ABC cần vẽ.
Ví dụ 5: Chứng minh hình dưới đây là tam giác đều
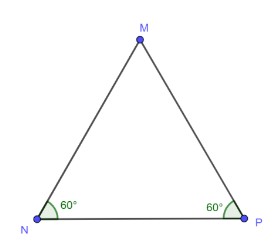
Áp dụng định lý tổng ba góc trong tam giác MNP có:
Góc M + Góc N + Góc P = 180 độ
Theo hình, Góc N = Góc P = 60 độ
Suy ra: Góc M = 180 – 60 – 60 = 60 độ
Suy ra: Góc M = Góc N = Góc P = 60 độ
Vậy tam gác MNP là tam giác đều vì có ba góc bằng nhau.
5.2. Bài tập áp dụng:
Bài 1: Cho ΔABC có góc B = 60°, AB = 2cm, BC = 5cm. Trên cạnh BC lấy điểm D sao cho BA = BD
a) Chứng minh tam giác ABD là Δ đều
b) Gọi H là trung điểm của BD. Chứng minh AH⊥BD
c) Tính độ dài AC
Bài 2: Cho tam giác ABC vuông tại A có ![]() . Vẽ Cx vuông góc BC, trên tia Cx lấy điểm E sao cho CE = CA (CE , CA nằm cùng phía đối BC). trên tia đối của tia BC lấy điểm F sao cho BF = BA. Chứng minh :
. Vẽ Cx vuông góc BC, trên tia Cx lấy điểm E sao cho CE = CA (CE , CA nằm cùng phía đối BC). trên tia đối của tia BC lấy điểm F sao cho BF = BA. Chứng minh :
a. Tam giác ACE đều
b. A, E, F thẳng hàng.
Bài 3: Cho sáu tam giác đều có cùng độ dài cạnh là 3 cm , ghép thành một hình lục giác đều có độ dài cạnh là bao nhiêu?
A. 3 cm
B. 6 cm
C.9 cm
D.12 cm
Bài 4: “Số đo các góc của hình lục giác đều … số đo các góc của hình tam giác đều”. Điền từ còn thiếu vào chỗ trống để được câu đúng.
A. bằng.
B. gấp đôi.
C. nhỏ hơn.
D. lớn hơn.
Trên đây là tổng hợp những kiến thức liên quan đế tam giác đều, mong rằng nó sẽ hữu ích đối với các bạn sinh viên trên hành trình làm chủ vốn kiến thức của mình.




