Lý thuyết Hệ thức Vi-ét và ứng dụng |Chuyên đề Toán 9

1. Lý thuyết Hệ thức Vi-ét |Chuyên đề Toán 9: 

Phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) có nghiệm dù đó là hai nghiệm phân biệt hay nghiệm kép thì ta đều có thể viết được dưới dạng:

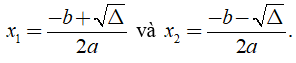
Khi đó nếu x₁, x₂ là hai nghiệm của phương trình ax² + bx + c = 0 (a ≠ 0) thì ta có:

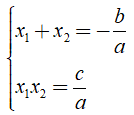
2. Ứng dụng Hệ thức Vi-ét |Chuyên đề Toán 9: 

a) Tính nhẩm nghiệm

– Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì phương trình có một nghiệm là x₁ = 1 và nghiệm còn lại là x₂ = c/a

– Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có a – b + c = 0 thì phương trình có một nghiệm là x₁ = -1 và nghiệm còn lại là x₂ = -c/a

b) Tìm hai số khi biết tổng và tích.

– Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình bậc hai x² – Sx + P = 0

– Điều kiện để có hai số đó là S² – 4P ≥ 0

3. Câu hỏi trắc nghiệm vận dụng liên quan có đáp án chi tiết: 

Câu hỏi 1: Biết rằng phương trình mx2 + (3m − 1)x + 2m − 1 = 0 (m ≠ 0) luôn có nghiệm x1; x2 với mọi m. Tìm x1; x2 theo m

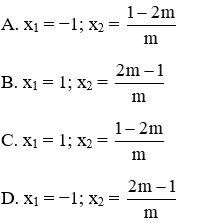
Lời giải chi tiết:

Phương trình mx2 + (3m − 1)x + 2m − 1 = 0 (m ≠ 0) có

a = m; b = 3m – 1; c = 2m – 1

Vì a – b + c = m – 3m + 1 + 2m – 1 = 0 nên phương trình có hai nghiệm

Đáp án cần chọn là: A

Câu hỏi 2: Chọn phát biểu đúng. Phương trình ax2 + bx + c (a ≠ 0) có hai nghiệm x1; x2. Khi đó:

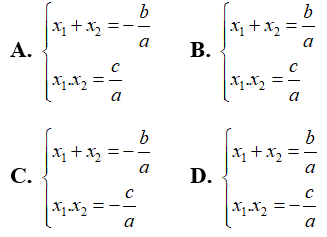
Lời giải chi tiết:

Cho phương trình bậc hai ax2 + bx + c (a ≠ 0).

Nếu x1; x2 là hai nghiệm của phương trình thì:

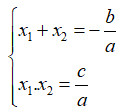
Chọn đáp án A.

Câu hỏi 3: Chọn phát biểu đúng: Phương trình ax2 + bx + c (a ≠ 0) có a – b + c = 0 . Khi đó:

A. Phương trình có một nghiệm x1 = 1, nghiệm kia x2 = c/a

B. Phương trình có một nghiệm x1 = -1, nghiệm kia x2= c/a

C. Phương trình có một nghiệm x1 = -1, nghiệm kia x2 = -c/a

D. Phương trình có một nghiệm x1 = 1, nghiệm kia x2 = -c/a

Lời giải chi tiết:

Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có a + b + c = 0

Thì phương trình có một nghiệm x1 = 1, nghiệm kia x2 = c/a

Nếu phương trình ax2 + bx + c (a ≠ 0) có a – b + c = 0

Thì phương trình có một nghiệm x1 = -1, nghiệm kia x2 = -c/a

Chọn đáp án C.

Câu hỏi 4: Cho hai số có tổng là S và tích là P với S2 ≥ 4P. Khi đó hai số đó là hai nghiệm của phương trình nào dưới đây:

A. X2 – PX + S = 0

B. X2 – SX + P = 0

C. SX2 – X + P = 0

D. X2 – 2SX + P = 0

Lời giải chi tiết:

Nếu hai số có tổng là S và tích là P thì hai số đó là hai nghiệm của phương trình X2 – SX + P = 0 (ĐK: S2 ≥ 4P)

Chọn đáp án B.

Câu hỏi 5: Không giải phương trình, tính tổng hai nghiệm (nếu có) của phương trình x2 – 6x + 7 = 0

A. 1/6

B. 3

C. 6

D. 7

Lời giải chi tiết:

Phương trình x2 – 6x + 7 = 0 có Δ = (-6x)2 – 4.1.7 = 8 > 0 nên phương trình có hai nghiệm x1; x2

Theo hệ thức Vi-ét ta có: x1 + x2 = = 6 ⇔ x1 + x2 = 6

Chọn đáp án C.

Câu hỏi 6: Gọi x1; x2 là nghiệm của phương trình x2 – 5x + 2 = 0. Không giải phương trình, tính giá trị của biểu thức A = x12 + x22

A. 20

B. 21

C. 22

D. 23

Lời giải chi tiết:

Phương trình x2 – 5x + 2 = 0 có hai nghiệm x1; x2

Theo hệ thức Vi-ét ta có:

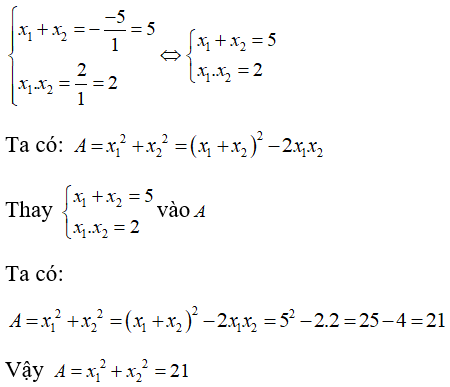
Chọn đáp án B.

Câu hỏi 7: Biết có hai số u và v thỏa mãn điều kiện: u + v = 12 và u.v = 27. Biết u < v. Tính u2.v?

A. 54

B. 27

C. 144

D. 72

Lời giải chi tiết:

Chọn đáp án A.

Câu hỏi 8: Biết có hai số u và v thỏa mãn u – v = 10 và u.v = 11. Tính |u+ v| ?

A. 11

B. 12

C. 10

D. 13

Lời giải chi tiết:

Ta có: u.v =11 nên u.(-v) = -11 (1)

Từ u – v = 10 nên u + (- v) = 10 (2)

Khi đó; u và (-v) là nghiệm phương trình:

x2 – 10x – 11 = 0 (*)

Do a – b + c = 1 -(-10 ) + (-11) = 0 nên phương trình (*) có 2 nghiệm là:

x1 = -1 và x2 = 11

* Trường hợp 1: Nếu u = -1 và –v = 11

=> v = -11 nên u + v = -12

* Trường hợp 2: nếu u = 11 và –v = -1 thì v = 1

Suy ra: u + v = 12

Trong cả 2 trường hợp ta có: |u + v| = 12

Chọn đáp án B.

Câu hỏi 9: Cho phương trình x2 – 4x + m + 1= 0 . Tìm m để phương trình trên có nghiệm và x1. x2 = 4. Tìm m ?

A. m = – 3

B. Không có giá trị nào

C. m =3

D. m = 2

Lời giải chi tiết:

Ta có: Δ’ = (-2)2 – 1.(m + 1) = 3 – m

Để phương trình đã cho có nghiệm thì Δ’ = 3 – m ≥ 0 ⇔ m ≤ 3 .

Với điều kiện trên thì phương trình đã cho có 2 nghiệm x1; x2 .

Theo hệ thức Vi-et ta có: x1.x2 = m + 1

Để x1. x2 = 4 thì m + 1 = 4 nên m = 3 ( thỏa mãn điều kiện)

Chọn đáp án C.

Câu hỏi 10: Cho phương trình x2 – 4x + (2m – 2) = 0.Tìm m để phương trình trên có 2 nghiệm dương phân biệt ?

A. m = 0

B. m =1

C. m = -1

D. Không có giá trị nào thỏa mãn

Lời giải chi tiết:

Ta có:

Δ’ = (-2)2 – 1.(2m – 2) = 2 – 2m

Để phương trình đã cho có hai nghiệm dương phân biệt khi và chỉ khi:

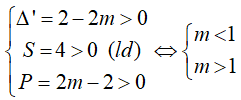
Suy ra không có giá trị nào của m thỏa mãn

Chọn đáp án D.

Câu hỏi 11: Cho phương trình x2 – (m + 1)x + m = 0. Có bao nhiêu giá trị nguyên của m để phương trình đã cho có 2 nghiệm âm?

A. 0

B. 1

C. 2

D. Vô số

Lời giải chi tiết:

Ta có:

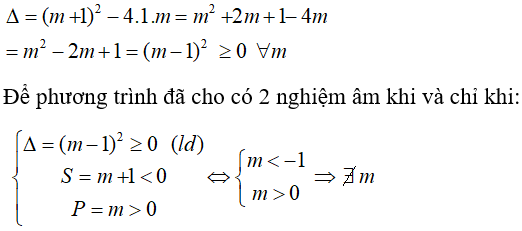
Chọn đáp án A.

Câu hỏi 12: Gọi x1; x2 là nghiệm của phương trình −x2 − 4x + 6 = 0. Không giải phương trình, tính giá trị của biểu thức Trắc nghiệm Hệ thức Vi-ét và ứng dụng có đáp án

A. −2         

B. 1            

C. 0            

D. 4

Lời giải chi tiết:

Phương trình: −x2 − 4x + 6 = 0 có ∆ = (−4)2 – 4.(− 1).6 = 40 > 0 nên phương trình có hai nghiệm x1; x2

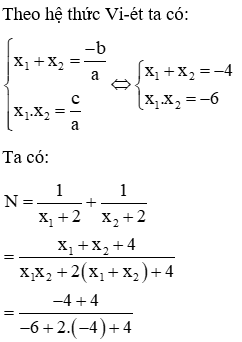
Đáp án cần chọn là: C

Câu hỏi 13: Gọi x1; x2 là nghiệm của phương trình x2 − 20x − 17 = 0. Không giải phương trình, tính giá trị của biểu thức C = x13 + x23

A. 9000      

B. 2090      

C. 2090      

D. 9020

Lời giải chi tiết:

Phương trình x2 − 20x − 17 = 0 có ∆ = 468 > 0 nên phương trình có hai nghiệm x1; x2

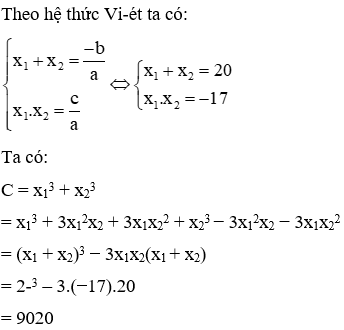
Đáp án cần chọn là: D

Câu hỏi 14: Gọi x1; x2 là nghiệm của phương trình 2×2 − 18x + 15 = 0. Không giải phương trình, tính giá trị của biểu thức C = x13 + x23

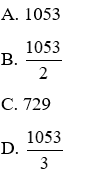
Lời giải chi tiết:

Phương trình 2×2 − 18x + 15 = 0 có  = 61 > 0 nên phương trình có hai nghiệm x1; x2

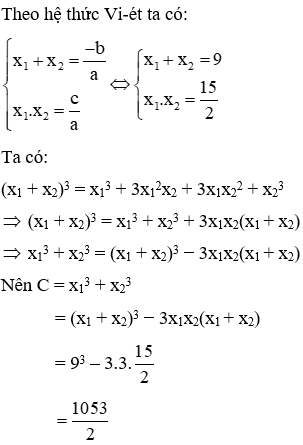
Đáp án cần chọn là: B

Câu hỏi 15: Biết rằng phương trình (m – 2)x2 – (2m + 5)x + m + 7 = 0 (m ≠ 2) luôn có nghiệm x1; x2 với mọi m. Tìm x1; x2 theo m

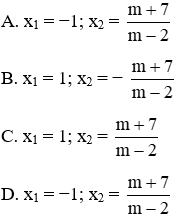
Lời giải chi tiết:

Phương trình (m – 2)x2 – (2m + 5)x + m + 7 = 0 có a = m – 2; b = − (2m + 5);

c = m + 7

Vì a + b + c = m – 2 – 2m – 5 + m + 7 = 0 nên phương trình có hai nghiệm

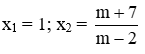
Đáp án cần chọn là: C