Đường tròn ngoại tiếp tam giác còn có thể được gọi với một cái tên khác là tam giác nội tiếp đường tròn (hay tam giác nằm trong đường tròn). Dưới đây là bài viết về Cách tính bán kính đường tròn ngoại tiếp tam giác dễ hiểu, mời các bạn cùng tham khảo.
Mục lục bài viết
- 1 1. Phương pháp sử dụng định lý Sin trong tam giác:
- 2 2. Phương pháp sử dụng diện tích tam giác:
- 3 3. Phương pháp sử dụng trong hệ tọa độ:
- 4 4. Phương pháp sử dụng trong tam giác vuông:
- 5 5. Bài tập, ví dụ minh họa có đáp án:
- 6 6. Đường tròn ngoại tiếp tam giác là gì? Tính chất của đường tròn ngoại tiếp tam giác?
1. Phương pháp sử dụng định lý Sin trong tam giác:
Cho tam giác ABC có BC = a, CA = b và AB = c, R là bán kính đường tròn ngoại tiếp tam giác ABC. Khi đó:
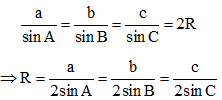
2. Phương pháp sử dụng diện tích tam giác:
Cho tam giác ABC có BC = a, CA = b và AB = c, R là bán kính đường tròn ngoại tiếp tam giác ABC. Khi đó:
![]()
3. Phương pháp sử dụng trong hệ tọa độ:
– Tìm tọa độ tâm O của đường tròn ngoại tiếp tam giác ABC
– Tìm tọa độ một trong ba đỉnh A, B, C (nếu chưa có)
– Tính khoảng cách từ tâm O tới một trong ba đỉnh A, B, C, đây chính là bán kính cần tìm
R = OA = OB = OC.
4. Phương pháp sử dụng trong tam giác vuông:
Tâm của đường tròn ngoại tiếp tam giác vuông được xác định là trung điểm của cạnh huyền, do đó bán kính đường tròn ngoại tiếp tam giác vuông chính bằng nửa độ dài cạnh huyền.
5. Bài tập, ví dụ minh họa có đáp án:
Ví dụ 1: Cho tam giác ABC có góc B bằng 45° và AC = 4. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Hướng dẫn giải:
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC.
Ta có: b = AC = 4
Áp dụng định lý sin trong tam giác ABC ta có:
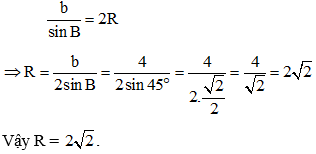
Ví dụ 2: Cho tam giác ABC có AB = 3, AC = 5 và BC = 6. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Hướng dẫn giải:
Theo công thức Hê – rông, diện tích tam giác ABC là:
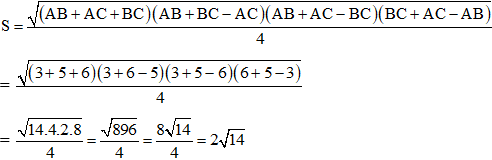
Bán kính đường tròn ngoại tiếp tam giác ABC là:
![]()
Ví dụ 3: Cho tam giác MNP có MN = 6, MP = 8 và PN = 10. Tính bán kính đường tròn ngoại tiếp tam giác MNP.
Ví dụ 4: Cho tam giác ABC vuông tại A có AB = 1; AC = 4. Gọi M là trung điểm AC.
a) Tính diện tích tam giác ABC.
b) Tính bán kính R1 của đường tròn ngoại tiếp tam giác ABC.
c) Tính bán kính R2 của đường tròn ngoại tiếp tam giác CBM.
Ví dụ 5: Cho tam giác ABC có BC = 10. Gọi (I) là đường tròn có tâm I thuộc cạnh BC và tiếp xúc với các cạnh AB, AC lần lượt tại M và N. Biết đường tròn (I) có bán kính bằng 3 và 2IB = 3IC. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.
Ví dụ 6: Cho tam giác ABC vuông tại A, Ab = 5cm, AC = 12cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Ví dụ 7: Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Chứng minh rằng 4 điểm A, B, C, D cùng nằm trên một đường tròn. Tính bán kính đường tròn đó.
Ví dụ 8: Cho hình vuông ACBD. Gọi M, N lần lượt là trung điểm của AB và BC. Gọi E là giao điểm của AM và DN
a) Tính số đo góc CEN
b) Chứng minh 4 điểm A, D, E, M thuộc cùng 1 đường tròn.
c) Xác định tâm đường tròn ngoại tiếp đi qua ba điểm B, D, E,.
Ví dụ 9: Cho tam giác ABC có AB = 3, AC = 5 và BC = 6. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Ví dụ 10: Cho hình thang vuông ABCD có , BC = 2AD = 2a. Gọi H là hình chiếu vuông góc của B lên AC, M là trung điểm của HC. Tìm tâm và bán kính của đường tròn ngoại tiếp tam giác BDM.
Hướng dẫn giải
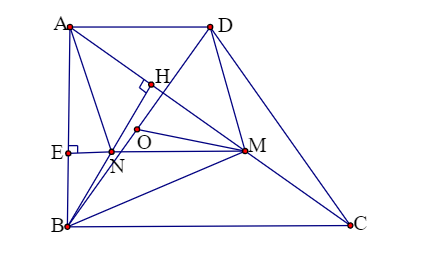
Gọi N là trung điểm của BH thì MN là đường trung bình của tam giác HBC => MN ⊥ AB
Mặt khác BH ⊥ AM
=> N là trực tâm của tam giác ABM
=> AN ⊥ BM
Do => MN //= AD
Nên ADMN là hình bình hành => AN // DM
Từ đó ta có: DM ⊥ MB hay tam giác DBM vuông tại M nên tâm đường tròn ngoại tiếp tam giác DBM là trung điểm O của BD
Ta có:
Ví dụ 11: Cho tam giác ABC vuông tại A, Ab = 5cm, AC = 12cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Ví dụ 12: Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Chứng minh rằng 4 điểm A, B, C, D cùng nằm trên một đường tròn. Tính bán kính đường tròn đó.
Ví dụ 13: Cho hình vuông ACBD. Gọi M, N lần lượt là trung điểm của AB và BC. Gọi E là giao điểm của AM và DN
a) Tính số đo góc CEN
b) Chứng minh 4 điểm A, D, E, M thuộc cùng 1 đường tròn.
c) Xác định tâm đường tròn ngoại tiếp đi qua ba điểm B, D, E,.
Ví dụ 14: Viết phương trình đường tròn nội tiếp của tam giác ABC khi đã cho sẵn tọa độ của 3 đỉnh A(-1;3); B(5;1); C(-2;3)
Ví dụ 15: Cho tam giác ABC đã biết A(1;3), B(-1;1), C(2;2). Tìm tọa độ của tâm đường tròn ngoại tiếp của tam giác ABC.
Ví dụ 16: Cho tam giác ABC đều với cạnh bằng 8cm. Xác định bán kính và tâm của đường tròn ngoại tiếp của tam giác ABC?
Ví dụ 17: Cho tam giác ABC đều với cạnh bằng 10cm. Xác định bán kính và tâm của đường tròn ngoại tiếp của tam giác ABC?
Ví dụ 18: Cho tam giác ABC vuông tại A, và AB=6 cm, BC=8 cm,. Xác định tâm và bán kính đường tròn ngoại tiếp tam giác ABC, Tính bán kính đường tròn ngoại tiếp của tam giác bằng bao nhiêu?
Ví dụ 19: Cho tam giác MNP có ba góc nhọn nội tiếp trong đường tròn (O; R). Ba đường của tam giác là MF, NE và PD cắt nhau tại H. Chứng minh tứ giác NDEP là tứ giác nội tiếp.
6. Đường tròn ngoại tiếp tam giác là gì? Tính chất của đường tròn ngoại tiếp tam giác?
Định nghĩa về đường tròn ngoại tiếp tam giác: Đường tròn ngoại tiếp tam giác được hiểu là đường tròn tiếp xúc phía ngoài của tam giác, là đường tròn đi qua 3 đỉnh của một tam giác. Tâm của đường tròn ngoại tiếp của tam giác được xác định là giao điểm của 3 đường trung trực của tam giác đó. Đường tròn ngoại tiếp tam giác còn có thể được gọi với một cái tên khác là tam giác nội tiếp đường tròn (hay tam giác nằm trong đường tròn).
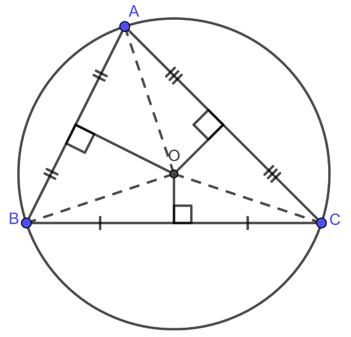
Khi tiến hành nối tâm O của đường tròn với 3 đỉnh của tam giác ABC thì sẽ có được các đường thẳng : OA = OB = OC. Đó chính là bán kính của đường tròn ngoại tiếp tam giác ABC mà chúng ta cần tìm. Với công thức này, các bạn học sinh có thể áp dụng để giải quyết khá nhiều các dạng bài liên quan đến đường tròn ngoại tiếp của tam giác.
Tính chất của đường tròn ngoại tiếp tam giác: Với đường tròn ngoại tiếp tam giác sẽ có các tính chất rất quan trọng mà các bạn học sinh cần nắm thật kỹ sau đây:
– Một tam giác thì chỉ có một và duy nhất một đường tròn ngoại tiếp.
– Giao điểm của ba đường trung trực của một tam giác bất kì chính là tâm của đường tròn ngoại tiếp tam giác đó.
– Đối với tam giác vuông thì trung điểm của cạnh huyền tam giác đó chính là tâm của đường tròn ngoại tiếp của tam giác.
– Với một tam giác đều thì tâm đường tròn ngoại tiếp và nội tiếp của tam giác đó sẽ cùng là 1 điểm.
Cách để vẽ được đường tròn ngoại tiếp tam giác chính xác: Để có thể xác định thật chính xác tâm của đường tròn ngoại tiếp tam giác thì các bạn học sinh cần nhớ thật kỹ kiến thức sau đây: “Tâm của đường tròn ngoại tiếp với bất kỳ một tam giác nào luôn là giao điểm của 3 đường trung trực tam giác đó”.
Vậy nên khi muốn vẽ đường tròn ngoại tiếp của tam giác ABC thì đầu tiên chúng ta cần vẽ tam giác, tiếp đó kẻ các đường trung trực xuất phát từ 3 đỉnh của tam giác đó để có thể xác định tâm I của đường tròn. Cuối cùng chỉ cần lấy bán kính R= IA= IB= IC. Vậy là chúng ta có thể vẽ được đường tròn ngoại tiếp tam giác rồi đó.




