Các dạng bài tập phương trình bậc hai có đáp án

1. Dạng giải phương trình: ax² + bx + c = 0 (a ≠ 0): 

Bước 1: Xác định các hệ số a; b; c (hoặc a; b’; c) của phương trình bậc hai ax² + bx + c.

Bước 2: Tính Δ = b² – 4ac (hoặc Δ’ = b’² – ac ).

+ TH1: Δ < 0, phương trình vô nghiệm.

+ TH2: Δ = 0, phương trình có nghiệm kép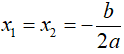

+ TH3: Δ > 0, phương trình có hai nghiệm phân biệt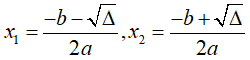

Bước 3: Tìm nghiệm của phương trình (nếu có).

Bước 4: Kết luận.

2. Dạng kiểm tra một giá trị x₀ có là nghiệm của phương trình: ax² + bx + c = 0 (a ≠ 0) hay không: 

Bước 1: Thay giá trị x₀ vào vế trái của phương trình: ax₀ + bx₀ + c

Bước 2: Kết luận.Tính vế trái. Nếu kết quả bằng 0 thì x₀ là một nghiệm của phương trình.

Bước 3: Kết luận.

Định lý Vi-ét: Nếu phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x₁, x₂ (phân biệt hoặc trùng nhau) thì tổng các nghiệm 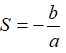và tích các nghiệm =.

=

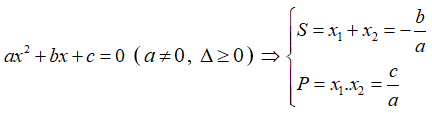
3. Dạng tìm tham số m để phương trình có nghiệm thỏa mãn điều kiện cho trước: 

Trong bài toán này, chúng ta cần tìm tham số m sao cho phương trình có thể có nghiệm thỏa mãn điều kiện đã cho trước. Để giải quyết bài toán này, ta có thể thực hiện các bước sau:

Bước 1: Đầu tiên, chúng ta cần xác định điều kiện cần để phương trình có thể có nghiệm. Điều kiện này có thể liên quan đến các hệ số của phương trình hoặc các ràng buộc đặc biệt.

Bước 2: Tiếp theo, chúng ta sẽ tính tổng S và tích P của hai nghiệm của phương trình. Điều này có thể được thực hiện bằng cách áp dụng định lý Vi-ét, một công thức quan trọng trong giải phương trình bậc hai.

Bước 3: Sau đó, chúng ta sẽ sử dụng hệ thức Vi-ét và kết hợp với các biến đổi đẳng thức, bất đẳng thức để tìm ra giá trị của tham số m. Qua quá trình này, chúng ta sẽ có thể giải được bài toán và tìm ra giá trị của tham số m.

Bước 4: Cuối cùng, chúng ta cần đối chiếu điều kiện đã tìm được với điều kiện ban đầu đã cho trước. Nếu điều kiện tìm được khớp với điều kiện ban đầu, ta có thể kết luận rằng giá trị của tham số m thỏa mãn yêu cầu đề bài.

Hi vọng qua quá trình này, bạn có thể hiểu rõ hơn về cách tìm tham số m để phương trình có nghiệm thỏa mãn điều kiện cho trước.

4. Dạng tìm tham số và tìm nghiệm còn lại khi biết trước một nghiệm x0 của phương trình:

Bước 1: Thay giá trị x0 vào phương trình để tìm tham số.

Trong bước này, chúng ta sẽ thay thế giá trị của nghiệm x0 vào phương trình ban đầu. Bằng cách làm như vậy, ta có thể tìm được giá trị của các tham số trong phương trình.

Bước 2: Thay giá trị của tham số hệ thức Vi-ét để tìm nghiệm còn lại.

Sau khi đã tìm được giá trị của các tham số từ bước 1, chúng ta sẽ thay thế các giá trị đó vào hệ thức Vi-ét. Bằng cách làm như vậy, ta có thể tìm được nghiệm còn lại của phương trình.

Bước 3: Kết luận.

Sau khi đã thực hiện các bước trên, chúng ta đã tìm được tham số và nghiệm còn lại của phương trình. Qua đó, chúng ta có thể kết luận và đưa ra kết quả cuối cùng của bài toán.

5. Dạng khi phương trình bậc hai có nghiệm, tìm hệ thức liên hệ giữa các nghiệm không phụ thuộc vào tham số:

Bước 1: Để phương trình có nghiệm, chúng ta cần tìm điều kiện phải thỏa mãn. Điều này có thể liên quan đến các hệ số của phương trình hoặc các ràng buộc khác.

Bước 2: Sau khi tìm được nghiệm, chúng ta có thể tính tổng S và tích P của hai nghiệm đó dựa trên định lý Vi-ét. Tổng S là tổng các nghiệm và tích P là tích của các nghiệm.

Bước 3: Tiếp theo, chúng ta có thể tính toán một giá trị m mới dựa trên tổng S và tích P. Giá trị m này có thể giúp chúng ta xác định mối quan hệ giữa hai nghiệm.

Bước 4: Tiếp theo, chúng ta có thể khử m và tìm ra một hệ thức liên hệ giữa hai nghiệm. Hệ thức này sẽ không phụ thuộc vào tham số và chỉ dựa trên tổng S, tích P và giá trị m đã tính được.

Bước 5: Cuối cùng, chúng ta rút ra kết luận từ các bước trên và nhận thức rõ ràng về mối quan hệ giữa các nghiệm của phương trình bậc hai.

6. Dạng áp dụng hệ thức Vi-ét để tính nhẩm nghiệm của phương trình bậc hai: 

Cho phương trình bậc hai ax² + bx + c = 0 (a ≠ 0).

+) Nếu a + b + c = 0 thì phương trình có nghiệm x₁ = 1 và x₂ = c/a

+) Nếu a – b + c = 0 thì phương trình có nghiệm x₁ = -1 và x₂ = -c/a.

7. Dạng tìm hai số khi biết tổng và tích: 

Nếu hai số u và v có tổng u + v = S và tích u.v = P thì hai số đó là nghiệm của phương trình x² – Sx + P = 0 .

Điều kiện để có u và v là S² – 4P ≥ 0.

8. Dạng giải và biện luận phương trình theo tham số m: 

Bước 1: Xác định các hệ số a; b; c (hoặc a; b’; c).

Bước 2: Giải phương trình theo m:

+) Với giá trị của m mà a = 0, giải phương trình bậc nhất.

+) Với giá trị của m mà a ≠ 0, giải phương trình bậc hai: Tính Δ = b’² – ac (hoặc Δ’ = b² – 4ac), xét các trường hợp của Δ chứa tham số và tìm nghiệm theo tham số.

Bước 3: Kết luận.

Biện luận phương trình:

– Phương trình có nghiệm khi:

+) Với giá trị của m mà a = 0, phương trình bậc nhất có nghiệm.

+) Với giá trị của m mà a ≠ 0, phương trình bậc hai có nghiệm.

– Phương trình có một nghiệm khi:

+) Với giá trị của m mà a = 0, phương trình bậc nhất có nghiệm.

+) Với giá trị của m mà a ≠ 0, phương trình bậc hai có nghiệm kép.

– Phương trình có hai nghiệm phân biệt khi: Giá trị của m mà a ≠ 0, phương trình bậc hai có hai nghiệm phân biệt.

Trên đây là quy trình giải và biện luận phương trình theo tham số m. Quy trình này giúp chúng ta xác định được các trường hợp và tính toán nghiệm của phương trình dựa trên giá trị của tham số. Hy vọng nội dung trên đã giúp bạn hiểu rõ hơn về cách giải và biện luận phương trình theo tham số m.

9. Dạng xác định dấu các nghiệm của phương trình: 

Bước 1: Xác định hệ số.

Bước 2: Tính Δ = b² – 4ac (hoặc Δ’ = b² – 4ac) để kiểm tra phương trình có nghiệm hay không.

Bước 3: Trong trường hợp phương trình có nghiệm (Δ ≥ 0 hoặc Δ’ ≥ 0), tính tổng S và tích P của hai nghiệm theo định lý Vi-ét để xét dấu các nghiệm của phương trình.

+) Phương trình có hai nghiệm cùng dấu: P > 0.

+) Phương trình có hai nghiệm dương: .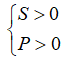

+) Phương trình có hai nghiệm âm: =.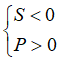

+) Phương trình có hai nghiệm trái dấu: P < 0.

Chú ý: Phương trình có hai nghiệm trái dấu chỉ cần xét P < 0 hoặc a.c < 0.

Bước 4: Kết luận.

10. Dạng tìm m để phương trình có nghiệm thỏa mãn điều kiện về dấu hoặc thỏa mãn đẳng thức, bất đẳng thức liên hệ giữa các nghiệm: 

Trong quá trình giải phương trình, chúng ta sẽ thực hiện một số bước để tìm ra giá trị của m sao cho phương trình thỏa mãn các điều kiện về dấu hoặc đẳng thức, bất đẳng thức giữa các nghiệm.

Bước 1: Đầu tiên, chúng ta cần xác định điều kiện a ≠ 0 (nếu cần) và điều kiện để phương trình có nghiệm. Điều này đảm bảo rằng phương trình không bị phân chia cho 0 và có thể có nghiệm.

Bước 2: Tiếp theo, chúng ta tính tổng S và tích P của hai nghiệm bằng cách sử dụng định lý Vi-ét. Định lý này cho phép chúng ta kết nối giữa các hệ số và các nghiệm của phương trình.

Bước 3: Sau đó, chúng ta sử dụng hệ thức Vi-ét và kết hợp với các biến đổi đẳng thức, bất đẳng thức để tìm ra các giá trị của tham số m. Việc này giúp chúng ta xác định được điều kiện để phương trình có nghiệm thỏa mãn yêu cầu về dấu hoặc thỏa mãn đẳng thức, bất đẳng thức.

Bước 4: Cuối cùng, chúng ta đối chiếu các điều kiện đã tìm được với yêu cầu ban đầu và rút ra kết luận về giá trị của m để phương trình có nghiệm thỏa mãn yêu cầu đặt ra.

Qua các bước trên, chúng ta có thể tìm ra giá trị của m sao cho phương trình có nghiệm thỏa mãn các điều kiện về dấu hoặc đẳng thức, bất đẳng thức giữa các nghiệm.

11. Dạng tìm tham số m để phương trình có một nghiệm là x0: 

Bước 1: Đầu tiên, chúng ta cần thay giá trị của x0 vào phương trình ban đầu để tìm ra giá trị của tham số m. Bằng cách này, ta có thể xác định một giá trị cụ thể cho m sao cho phương trình có thể có một nghiệm duy nhất là x0.

Bước 2: Tiếp theo, chúng ta thay giá trị của tham số m vào phương trình hoặc sử dụng hệ thức Vi-ét để tìm ra các nghiệm còn lại của phương trình. Qua quá trình này, chúng ta có thể xác định được tất cả các giá trị của x mà phương trình có thể có.

Bước 3: Cuối cùng, sau khi tìm được giá trị của tham số m và các nghiệm của phương trình, chúng ta có thể sử dụng các giá trị này để kiểm tra tính đúng đắn của phương trình. Bằng cách này, chúng ta có thể đưa ra kết luận cuối cùng về việc phương trình có nghiệm x0 hay không.

12. Dạng tìm giá trị của tham số để hai phương trình có ít nhất một nghiệm chung:

Để tìm giá trị của tham số sao cho hai phương trình có ít nhất một nghiệm chung, chúng ta cần thực hiện một số bước sau:

Bước 1: Đầu tiên, hãy xác định điều kiện để các phương trình có thể có nghiệm chung. Điều này có thể liên quan đến các hệ số của các phương trình hoặc các ràng buộc khác.

Bước 2: Tiếp theo, chúng ta cần tìm ra nghiệm chung của các phương trình và tìm giá trị của tham số tương ứng. Để làm điều này, chúng ta có thể giả sử một giá trị cụ thể cho một biến (ví dụ: x0) và sau đó lập hệ phương trình với hai ẩn (x0 và tham số) để giải quyết hệ phương trình này.

Bước 3: Sau khi tìm được các giá trị của tham số, chúng ta cần so sánh kết quả với điều kiện ban đầu đã được đặt ra để xác định xem chúng có đáp ứng yêu cầu hay không. Dựa vào sự so sánh này, chúng ta có thể rút ra kết luận cuối cùng về giá trị của tham số mà chúng ta đang tìm kiếm.

Hãy nhớ rằng quá trình tìm giá trị của tham số có thể phức tạp và đòi hỏi sự kiên nhẫn và quan sát kỹ càng. Tuy nhiên, bằng cách tuân thủ các bước trên, chúng ta có thể xác định giá trị của tham số mà đáp ứng yêu cầu của hai phương trình có ít nhất một nghiệm chung.