Giải bài Tia số, số liền trước, số liền sau (Toán lớp 2 bài 2)

1. Bài tập vận dụng Tia số, số liền trước, số liền sau:

Bài 1: Trừ 8 từ 10 trên tia số

Lời giải

Trừ 8 từ 10 trên tia số là một phép tính đơn giản trong toán học. Để thực hiện phép tính này, ta chỉ cần di chuyển từ điểm 10 trên tia số về bên trái 8 đơn vị, và ta sẽ đến được điểm 2. Điểm 2 chính là kết quả của phép trừ 8 từ 10. Ta có thể viết lại phép tính này dưới dạng biểu thức: 10 – 8 = 2. 

Bài 2: Số sau số 0 là gì?

Lời giải:

Nếu chúng ta nhìn vào tia số, chúng ta sẽ thấy rằng số liền trước số 0 là số 1. Số 1 là số nguyên dương nhỏ nhất, và nó nằm ngay bên phải của số 0. Để đi từ số 0 đến số 1, chúng ta phải di chuyển một đơn vị sang phải.

Bài 3: Thực hiện phép nhân 5 x 2 bằng tia số

Lời giải

Phép nhân 5 x 2 có thể được thực hiện bằng cách sử dụng tia số. Để nhân 5 x 2, ta có thể vẽ một tia số có 5 đoạn thẳng, mỗi đoạn có độ dài bằng 2. Sau đó, ta có thể đếm tổng số điểm nối giữa các đoạn thẳng để tìm kết quả. Kết quả là 10, vì có 10 điểm nối trên tia số. 

Bài 4: So sánh 7 và 13 bằng cách sử dụng tia số

Lời giải

Để so sánh 7 và 13, ta có thể vẽ hai điểm trên tia số tương ứng với hai số đó. Điểm 7 nằm bên trái của điểm 13, nghĩa là nó gần gốc hơn. Điều này cho ta biết rằng 7 nhỏ hơn 13. Ta có thể viết 7 < 13 để thể hiện mối quan hệ này. 

Bài 5: Sử dụng tia số để thực hiện phép chia 8 ÷ 4

Lời giải

Để thực hiện phép chia 8 ÷ 4 bằng cách sử dụng tia số, bạn cần làm như sau:

– Bước 1: Vẽ một đoạn thẳng AB có độ dài bằng 8 đơn vị. Đánh dấu điểm A là điểm bắt đầu của tia số và điểm B là điểm kết thúc của tia số.

– Bước 2: Chia đoạn thẳng AB thành 4 phần bằng nhau bằng cách dùng thước kẻ hoặc compa. Đánh dấu các điểm chia là C, D, E theo thứ tự từ A đến B. Mỗi phần có độ dài bằng 2 đơn vị.

– Bước 3: Vẽ một tia số khác CD vuông góc với tia số AB tại điểm C. Đánh dấu điểm F trên tia số CD sao cho CF bằng CE. Điểm F là điểm kết quả của phép chia.

– Bước 4: Đọc kết quả của phép chia từ điểm A đến điểm F trên tia số CD. Kết quả là 2 đơn vị.

Vậy, phép chia 8 ÷ 4 bằng cách sử dụng tia số cho kết quả là 2.

Bài 6: Sử dụng tia số để so sánh 5 và 6

Lời giải

Để so sánh 5 và 6, ta có thể vẽ hai điểm trên tia số tương ứng với hai số đó. Điểm 5 nằm bên trái của điểm 6, nghĩa là nó gần gốc hơn. Điều này cho ta biết rằng 5 nhỏ hơn 6. Ta có thể viết 5 < 6 để thể hiện mối quan hệ này. 

2. Tia số là gì?

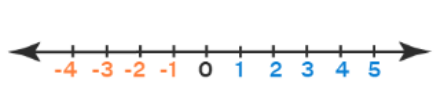
Tia số là hình biểu diễn trực quan của các số trên một đường thẳng vẽ theo chiều ngang hoặc chiều dọc. Viết các số trên tia số giúp chúng ta dễ dàng so sánh và thực hiện các phép tính số học cơ bản trên chúng. Số 0 được coi là gốc của một tia số. Các số bên trái số 0 là số âm, các số bên phải số 0 đều là số dương. Vì vậy, có thể nói rằng trên tia số, khi chúng ta di chuyển về phía bên phải, giá trị của các số sẽ tăng lên. Điều này có nghĩa là các số ở bên phải lớn hơn các số ở bên trái. Ví dụ: 3 đứng bên phải 1, do đó 3 > 1. Quan sát tia số ngang dưới đây.

*Cách vẽ một tia số

Để vẽ một tia số hoặc vẽ một số trên đó, chúng ta thực hiện các bước sau.

– Bước 1: Vẽ một đường ngang có mũi tên ở hai đầu. (Bạn cũng có thể vẽ đường số dọc)

– Bước 2: Chọn thang đo tùy theo số đã cho. Ví dụ: nếu phải vẽ ô số 5 thì bạn có thể chọn thang đo là 1. Nếu phải vẽ ô số 50, bạn có thể chọn thang đo là 5, 10 hoặc 25. (Việc xác định thang đo phù hợp phụ thuộc vào các yếu tố của số đã cho)

– Bước 3: Đánh dấu các điểm ở những khoảng cách bằng nhau. Vì vậy, nếu bạn đã chọn 1 làm thang đo thì hãy đánh dấu 0, 1, 2, 3, 4, v.v.

– Bước 4: Tìm số đã cho. Đánh dấu điểm đó bằng một vòng tròn.

3. Số liền trước và số liền sau trên một tia số:

Trong toán học, số liền trước và số liền sau của một số nguyên là hai số nguyên liền kề nó trên tia số. Ví dụ, số liền trước của 5 là 4, và số liền sau của 5 là 6. Để tìm số liền trước hoặc số liền sau của một số nguyên, ta có thể cộng hoặc trừ 1 với nó. Ví dụ, để tìm số liền sau của 2, ta có thể cộng 1 với 2 và được 3. Để tìm số liền trước của 2, ta có thể trừ 1 với 2 và được 1. Số liền trước và số liền sau của một số nguyên có thể được biểu diễn bằng các điểm trên tia số. Ví dụ, nếu ta vẽ một tia số với điểm 0 là gốc, ta có thể đặt các điểm cho các số nguyên như sau:

Trong hình này, điểm 3 biểu diễn số nguyên 3, điểm 4 biểu diễn số liền sau của 4, và điểm 2 biểu diễn số liền trước của 3. Ta có thể nhận thấy rằng các điểm càng gần nhau trên tia số thì các số nguyên tương ứng càng gần nhau về giá trị.

4. Các phép toán trên một tia số:

4.1. Phép cộng:

Khi ta cộng hai số dương thì kết quả luôn là số dương. Do đó, khi cộng các số dương hướng chuyển động sẽ luôn về bên phải.

Ví dụ: phép cộng 1 và 5 (1 + 5 = 6)

Ở đây số thứ nhất là 1 và số thứ hai là 5; cả hai đều dương. Đầu tiên, xác định vị trí số 1 trên tia số. Sau đó di chuyển 5 vị trí sang phải sẽ được 6.

4.2. Phép trừ:

Khi trừ hai số dương, hãy di chuyển sang trái cho đến giá trị của số thứ hai.

Ví dụ: trừ 5 từ 7

Ở đây số thứ nhất là 7 và số thứ hai là 5; cả hai đều dương. Đầu tiên, xác định vị trí số 7 trên trục số. Sau đó di chuyển 5 vị trí sang trái sẽ được 2.

4.3. Phép nhân:

Vì phép nhân thực sự là phép cộng lặp đi lặp lại nên chúng ta cũng có thể điều chỉnh mô hình phép cộng của mình để trở thành mô hình nhân. Hãy nghĩ về 3 × 4. Điều này có nghĩa là cộng bốn với chính nó ba lần:

3 × 4 = 4 + 4 + 4.

Vì vậy, để nhân trên tia số, chúng ta thực hiện phép cộng nhiều lần.

4.4. Phép chia:

* Ví dụ: thực hiện phép chia 15 ÷ 5 là:

Xét trên tia số, ta có thể đưa về bài toán như sau cho dễ hiểu:

Mai bước 5 bước một lần. Nếu Mai chạm tới số 15 thì cô ấy đã bước được 5 bước bao nhiêu lần?

Để giải bài toán chia trên tia số, Mai bắt đầu từ số 0, hướng về chiều dương. Cô ấy đi về phía trước số bước được cho bởi số thứ hai (số chia). Mai lặp lại quá trình đó cho đến khi đạt được số đầu tiên. Số lần Mai lặp lại quá trình sẽ cho ra thương số của hai số.

15 ÷ 5 = 3

5. Các tác dụng của tia số:

– Công cụ đắc lực trong lớp học toán tiểu học

Các công cụ đơn giản đã được sử dụng để giúp thực hiện những bước nhảy vọt trong việc hiểu hoặc giải thích những ý tưởng mới trong khoa học, toán học và công nghệ. Một trong những “phát minh” quan trọng nhất của toán học là tia số. Khoảng 2.500 năm trước, người Ai Cập cổ đại được cho là đã tạo ra dãy số rất thực tế. Họ buộc những nút thắt có khoảng cách bằng nhau dọc theo một sợi dây dùng để đo chiều dài bằng cách đếm số khoảng trống. Ví dụ, người Ai Cập đo dây đã tạo thành một hình tam giác có 3 khoảng trống, 4 khoảng trống và 5 khoảng trống dọc theo mỗi cạnh. Sợi dây có một chiều dài duy nhất nên nó có thể được sử dụng để đo các tòa nhà, bức tường hoặc cánh đồng.

Sợi dây là một công cụ trực quan hoạt động tốt với những thứ thực tế. Nó rất tốt cho việc đo lường cũng như tính toán liên quan đến các phép toán “thẳng tiến” như phép cộng và phép nhân. 

– Biểu diễn số âm

Công lao tạo ra tia số để hiển thị các số nhỏ hơn 0 đã được trao cho người Anh John Wallis. Trong những hình minh họa đầu tiên của mình, anh ấy đã sử dụng một đường liền nét cho số 0 và các số dương và một đường chấm chấm cho các số âm.

Cùng lúc đó, nhà toán học người Hà Lan Rene’ Descartes đã sử dụng hai đường thẳng để tạo ra hệ tọa độ x-y nhằm củng cố phương pháp mà Wallis đã sử dụng. Việc sử dụng tia số cung cấp cách hiển thị số âm và quan trọng hơn là những công cụ này được sử dụng để liên kết tất cả các số với nhau. Với những công cụ này, chúng ta đã đạt được những bước tiến lớn trong việc khám phá những ý tưởng toán học mới vì đã có cách để làm việc với các con số chỉ bằng một mô hình trực quan duy nhất!

– Tia số trong lớp học

Khi tia số lần đầu tiên được sử dụng trong lớp học, người ta đã nảy ra một ý tưởng hay là hiển thị một trục kéo dài theo cả hai hướng mà không đề cập đến vế trái của số 0 (gốc). Nếu 0 được hiển thị là điểm cuối thì ví dụ này là một tia chứ không phải một đường thẳng.

Khoảng cách từ 0 đến 1 được gọi là độ dài đơn vị (hoặc một đơn vị) mang lại ý nghĩa cho tất cả các số dọc theo đường thẳng. Ví dụ, biết độ dài của một đơn vị có nghĩa là việc nhân đôi hoặc nhân ba khoảng cách đó sẽ tạo ra cách giải thích 2 hoặc 3 đơn vị. Đánh dấu khoảng cách từ 0 đến một điểm nhỏ hơn 1 sẽ cho khoảng cách có thể được viết dưới dạng phân số hoặc số thập phân nhỏ hơn 1. Khoảng cách từ 0 đến 1 có thể có độ dài bất kỳ, nhưng một khi nó được xác định, giá trị của tất cả các số khác sẽ được quyết định.