Đồ thị hàm số y= ax b (a ≠ 0) (Bài tập chuyên đề Toán 9)

1. Hàm số y = ax + b:

Để giải thích chi tiết hàm số y = ax + b, ta cần xét đến các khái niệm sau:

– Hệ số góc a: là hệ số của x trong biểu thức y = ax + b, cho biết độ dốc của đường thẳng. Nếu a > 0, đường thẳng có xu hướng tăng khi x tăng; nếu a < 0, đường thẳng có xu hướng giảm khi x tăng.

– Hệ số tự do b: là hằng số trong biểu thức y = ax + b, cho biết giá trị của y khi x = 0, hay nói cách khác là điểm cắt của đường thẳng với trục tung. Nếu b > 0, đường thẳng cắt trục tung ở phía trên gốc tọa độ; nếu b < 0, đường thẳng cắt trục tung ở phía dưới gốc tọa độ.

– Phương trình chính tắc: là phương trình có dạng y = ax + b, cho biết mối quan hệ giữa x và y trong hàm số. Nếu biết giá trị của x, ta có thể tính được giá trị của y tương ứng, và ngược lại.

– Phương trình tổng quát: là phương trình có dạng ax + by + c = 0, cho biết mối quan hệ giữa các hệ số a, b, c và các biến x, y trong hàm số. Nếu biết giá trị của hai trong ba hệ số a, b, c, ta có thể tìm được phương trình chính tắc của hàm số.

– Giao điểm với các trục: là các điểm thuộc đồ thị của hàm số mà có một tọa độ bằng 0. Để tìm giao điểm với trục tung, ta cho x = 0 và tính y từ phương trình chính tắc; để tìm giao điểm với trục hoành, ta cho y = 0 và giải phương trình chính tắc để tìm x.

Nếu a và b là các số thực cố định, a ≠ 0 thì f(x) = ax + b với x ∈ ℝ được gọi là hàm tuyến tính. Nếu a = 0 thì f(x) = b được gọi là hằng số

Đôi khi các hàm tuyến tính được viết là y = ax + b.

Ví dụ 1: f(x) = 2x +1 là hàm tuyến tính với a = 2 và b = 1

Ví dụ 2: f(x) = 3 là hàm hằng.

2. Đồ thị hàm số y = ax + b:

* Cách vẽ đồ thị hàm số

Đồ thị hàm số y = ax + b (a ≠ 0) là một đường thẳng có hệ số góc là a và độ lệch là b. Để vẽ đồ thị hàm số này, ta cần tìm hai điểm thuộc đường thẳng và nối chúng bằng một đoạn thẳng. Có hai cách đơn giản để tìm hai điểm thuộc đường thẳng:

– Cách 1: Tìm giao điểm của đường thẳng với trục hoành và trục tung. Giao điểm của đường thẳng với trục hoành là điểm có tọa độ (x, 0) thỏa mãn phương trình y = ax + b. Từ đó, ta có x = -b/a. Giao điểm của đường thẳng với trục tung là điểm có tọa độ (0, y) thỏa mãn phương trình y = ax + b. Từ đó, ta có y = b. Vậy, hai điểm thuộc đường thẳng là (-b/a, 0) và (0, b).

– Cách 2: Chọn một giá trị bất kỳ cho x và tính giá trị tương ứng của y theo phương trình y = ax + b. Lặp lại quá trình này với một giá trị khác của x để được một điểm khác thuộc đường thẳng. Ví dụ, nếu x = 1, ta có y = a + b. Nếu x = 2, ta có y = 2a + b. Vậy, hai điểm thuộc đường thẳng là (1, a + b) và (2, 2a + b).

Sau khi tìm được hai điểm thuộc đường thẳng, ta dùng thước kẻ nối chúng lại để được đồ thị hàm số y = ax + b.

* Các trường hợp của a ảnh hưởng đến dạng và vị trí của đồ thị như sau:

– Nếu a > 0, đồ thị có dạng nghiêng lên từ trái sang phải, cắt trục hoành tại điểm có hoành độ x = -b/a và cắt trục tung tại điểm có tung độ y = b. Đồ thị này có tính chất là khi x tăng thì y tăng và ngược lại.

– Nếu a < 0, đồ thị có dạng nghiêng xuống từ trái sang phải, cắt trục hoành tại điểm có hoành độ x = -b/a và cắt trục tung tại điểm có tung độ y = b. Đồ thị này có tính chất là khi x tăng thì y giảm và ngược lại.

– Nếu a = 0, đồ thị là một đường thẳng song song với trục hoành, cách trục hoành một khoảng b. Đồ thị này không phụ thuộc vào x, chỉ phụ thuộc vào b.

* Khi x = 0

Khi x = 0 của đồ thị hàm số y = ax + b (a ≠ 0), ta cần xét hai trường hợp:

– Nếu b = 0, thì đồ thị hàm số là một đường thẳng đi qua gốc tọa độ (0, 0) và có hệ số góc là a. Khi x = 0, ta có y = 0, nên điểm (0, 0) thuộc đồ thị hàm số.

– Nếu b ≠ 0, thì đồ thị hàm số là một đường thẳng song song với trục hoành và cắt trục tung tại điểm (0, b). Khi x = 0, ta có y = b, nên điểm (0, b) thuộc đồ thị hàm số.

Vậy, trường hợp x = 0 của đồ thị hàm số y = ax + b (a ≠ 0) phụ thuộc vào giá trị của b. Nếu b = 0, đồ thị hàm số cắt trục tung tại gốc tọa độ. Nếu b ≠ 0, đồ thị hàm số cắt trục tung tại điểm có tung độ bằng b.

* Khi f(x) = 0

Khi f(x) = 0 của đồ thị hàm số y= ax + b (a ≠ 0), ta cần hiểu rằng điều này có nghĩa là tìm các giá trị của x sao cho đồ thị hàm số cắt trục hoành. Điều này tương đương với việc giải phương trình ax + b = 0. Ta có thể dùng công thức x = -b/a để tìm nghiệm của phương trình.

– Nếu a > 0, đồ thị hàm số sẽ có dạng một đường thẳng có độ dốc dương, đi qua điểm cắt trục tung là (0, b) và điểm cắt trục hoành là (-b/a, 0).

– Nếu a < 0, đồ thị hàm số sẽ có dạng một đường thẳng có độ dốc âm, đi qua điểm cắt trục tung là (0, b) và điểm cắt trục hoành là (-b/a, 0).

Trong cả hai trường hợp, ta có thể vẽ đồ thị hàm số bằng cách nối hai điểm cắt trục.

3. Bài tập vận dụng:

Bài 1: Xác định xem mỗi hàm sau đây có phải là hàm tuyến tính hay không

A. f(x) – 1 = 3x

B. 3 = x – 2y

C. x + y = 1 – 3x

D. 2x² – 2x = y

Đáp án:

Lời giải: A. f(x) – 1 = 3x

Hàm số tuyến tính là hàm số có thể biểu diễn bằng một đường thẳng trên hệ trục tọa độ. Để xác định một hàm số là tuyến tính hay không, ta có thể dùng hai phương pháp: kiểm tra dạng tổng quát của hàm số hoặc kiểm tra tính chất cộng và nhân của hàm số. Theo phương pháp đầu tiên, một hàm số là tuyến tính nếu nó có dạng y = ax + b, trong đó a và b là các hằng số. Theo phương pháp thứ hai, một hàm số là tuyến tính nếu nó thỏa mãn hai tính chất sau: f(x + y) = f(x) + f(y) và f(kx) = kf(x), trong đó k là một hằng số. Áp dụng hai phương pháp này, ta có thể nhận ra rằng chỉ có hàm số A là hàm số tuyến tính, vì nó có dạng y = 3x – 1 và thỏa mãn hai tính chất cộng và nhân. Các hàm số còn lại không phải là hàm số tuyến tính, vì chúng không có dạng y = ax + b và không thỏa mãn hai tính chất cộng và nhân.

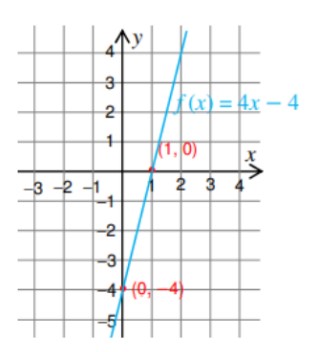
Bài 2: Vẽ đồ thị hàm số f(x) = 4x – 4

Lời giải:

Giao điểm x là cặp có thứ tự với y = 0. Tức là (1, 0).

Giao điểm y là cặp có thứ tự với x = 0. Tức là (0, –4).

Vẽ các giao điểm này trên một hệ tọa độ và vẽ một đường đi qua chúng.

Bạn cũng có thể sử dụng khái niệm độ dốc để vẽ đồ thị của hàm tuyến tính.

Để vẽ đồ thị của hàm tuyến tính f (x) = ax + b, trước tiên hãy đánh dấu điểm chặn y.

Sau đó, từ giao điểm y di chuyển một đơn vị lên (nếu a > 0) hoặc xuống một đơn vị (nếu a < 0) và sang bên phải một đơn vị và tìm một điểm. Sau đó kẻ đường thẳng đi qua điểm chặn y và điểm này. Đường này là đồ thị của hàm tuyến tính.

Bài 3: Đồ thị hàm số tuyến tính f(x) = 2 – 2x đồng biến hay nghịch biến?

Lời giải:

Đồ thị hàm số f(x) = 2 – 2x là một đường thẳng có hệ số góc bằng -2. Điều này có nghĩa là khi x tăng thì f(x) giảm và ngược lại. Do đó, đồ thị hàm số này là nghịch biến trên toàn miền xác định.

Ta thấy rằng đồ thị hàm số luôn đi xuống từ trái sang phải, cho dù x dương hay âm. Điều này chứng tỏ tính nghịch biến của hàm số.

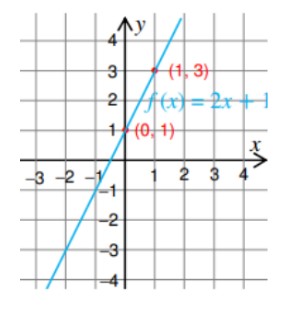
Bài 4: Vẽ đồ thị hàm số f(x) = 2x + 1.

Lời giải:

Độ dốc của đồ thị của hàm tuyến tính f (x) = 2x + 1 là 2 và tung độ gốc là (0, 1).

Nếu di chuyển 2 đơn vị lên từ điểm chặn y và một đơn vị ở bên phải, ta sẽ nhận được điểm (1, 3). Vậy đường thẳng đi qua (0, 1) và (1, 3) là đồ thị của hàm số f(x) = 2x + 1.

Bài 5: Cho hàm tuyến tính f (x) = 7x + 2, xác định tung độ y và hoành độ x.

Lời giải:

Hàm tuyến tính f (x) = 7x + 2 là một hàm số có đồ thị là một đường thẳng. Để xác định tung độ y và hoành độ x của một điểm bất kỳ trên đồ thị, ta có thể sử dụng công thức sau:

y = f (x) = 7x + 2

Trong đó, y là tung độ, x là hoành độ và f (x) là giá trị của hàm số tại x. Ví dụ, nếu x = 0, ta có:

y = f (0) = 7 * 0 + 2 = 2

Điều này có nghĩa là điểm có hoành độ x = 0 và tung độ y = 2 nằm trên đồ thị của hàm số. Tương tự, nếu y = 9, ta có:

9 = f (x) = 7x + 2

Để tìm x, ta phải giải phương trình:

7x + 2 – 9 = 0

⇒ x = (9 – 2) / 7

⇒ x = 1

Điều này có nghĩa là điểm có hoành độ x = 1 và tung độ y = 9 cũng nằm trên đồ thị của hàm số. Như vậy, ta có thể xác định tung độ và hoành độ của bất kỳ điểm nào trên đồ thị bằng cách sử dụng công thức y = f (x) và giải phương trình.