Độ lớn của lực Lorenxơ được tính theo công thức nào?

1. Công thức tính độ lớn của lực Lorenxơ:

Độ lớn của lực Lorenxơ là lực tác dụng lên một hạt mang điện tích q chuyển động với vận tốc v trong một trường từ đều có cảm ứng từ B. Lực này có phương vuông góc với mặt phẳng chứa v và B, và chiều theo quy tắc bàn tay trái. Độ lớn của lực Lorenxơ được tính theo công thức:

f = |q|vBsinα

Trong đó:

– f là độ lớn lực Lorenxơ, có đơn vị Niu tơn (N);

– q là điện tích, có đơn vị Cu lông (C);

– v là vận tốc của hạt điện tích, có đơn vị m/s;

– B là cảm ứng từ của trường từ, có đơn vị Tê xla (T);

– α là góc giữa vecto vận tốc và vecto cảm ứng từ.

Lực Lorenxơ có thể làm thay đổi phương và độ lớn của vận tốc của hạt mang điện tích, tùy thuộc vào góc α và chiều của điện tích q. Nếu α = 0° hoặc 180°, tức là vectơ vận tốc song song hoặc nghịch chiều với vectơ cảm ứng từ, thì f = 0, tức là không có lực Lorenxơ. Nếu α = 90°, tức là vectơ vận tốc vuông góc với vectơ cảm ứng từ, thì f = |q|vB, tức là lực Lorenxơ có độ lớn lớn nhất.

Ví dụ: Một hạt mang điện tích q = 2.10^-6 C chuyển động với vận tốc v = 3.10^4 m/s trong trường từ đều có cảm ứng từ B = 0,5 T. Góc giữa vecto v và vecto B là 60 độ. Tính độ lớn của lực Lorenxơ tác dụng lên hạt.

Lời giải:

Theo công thức trên, ta có:

f = |q|vBsinα

f = |2.10^-6| x 3.10^4 x 0,5 x sin60

f = 0,026 N

2. Khái quát về lực Lorenxơ:

Lực Lorenxơ có phương vuông góc với mặt phẳng chứa vectơ vận tốc và vectơ cảm ứng từ. Chiều của lực Lorenxơ được xác định bằng quy tắc bàn tay trái: Đặt bàn tay trái mở rộng sao cho các đường sức từ có thể xuyên vào lòng bàn tay, chiều từ cổ tay đến các ngón tay là chiều của vectơ vận tốc. Ngón cái choãi ra chỉ song song theo chiều của lực Lorenxơ tác dụng lên các hạt mang theo điện tích dương và chỉ chiều ngược lại nếu hạt mang điện tích âm.

Lực Lorenxơ có liên quan đến điện năng bởi vì nó là nguyên nhân của hiện tượng cảm ứng điện từ. Khi một dây dẫn mang dòng điện chuyển động trong trường từ, các hạt mang điện tích trong dây dẫn sẽ bị tác dụng bởi lực Lorenxơ. Lực này sẽ gây ra một điện thế cảm ứng trên hai đầu của dây dẫn, làm cho dòng điện chạy ngược lại. Điều này giải thích cho việc tạo ra điện năng từ các máy phát điện hoặc các máy biến áp.

Ví dụ: Một dây dẫn dài 1 m mang dòng điện I = 10 A chuyển động với vận tốc v = 2 m/s trong trường từ đều có cảm ứng từ B = 0,1 T. Góc giữa vecto v và vecto B là 90 độ. Tính điện thế cảm ứng trên hai đầu của dây dẫn.

Lời giải:

Theo công thức trên, ta có:

f = |q|vBsinα

f = |I.l|vBsinα

f = |10 x 1| x 2 x 0,1 x sin90

f = 2 N

Điện thế cảm ứng trên hai đầu của dây dẫn là:

U = f.l

U = 2 x 1

U = 2 V

3. Bài tập về lực Lorenxơ:

3.1. Lực tác động lên điện tích chuyển động trong từ trường: 

Ví dụ: Một hạt điện tích q di chuyển dọc theo y dương – hướng vận tốc một từ trường . Tính lực Lorentz mà hạt trải qua (a) khi từ trường dọc theo hướng y dương (b) khi từ trường chỉ theo z dương – hướng (c) khi từ trường ở mặt phẳng zy và tạo một góc θ với vận tốc của hạt. Đánh dấu hướng của lực từ trong từng trường hợp.

Cách giải:

Vận tốc của hạt là

(a) Từ trường dọc theo hướng y dương, điều này chỉ ra,

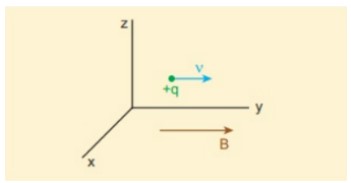
Theo lực Lorentz,

Vì vậy, không có lực tác động lên hạt khi nó di chuyển dọc theo hướng từ trường.

(b) Các điểm từ trường theo hướng z dương, điều này chỉ ra,

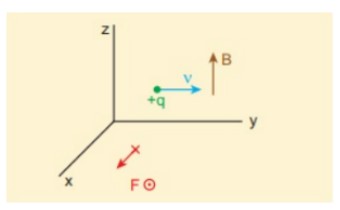
Theo lực Lorentz,

Do đó, cường độ của lực Lorentz là qvB và hướng dọc theo hướng x dương.

(c) Từ trường nằm trong mặt phẳng zy và tạo một góc θ với vận tốc của hạt, có nghĩa là

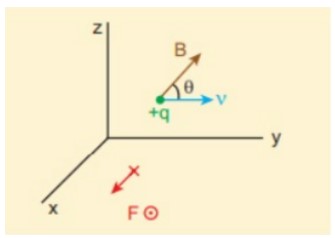
Theo lực Lorentz ,

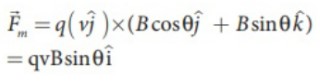
Ví dụ: Tính lực Lorentz cung cấp trên hạt điện tích q chuyển động với vận tốc . Tính góc giữa lực Lorentz và vận tốc của hạt tích điện, giải thích kết quả.

Lời giải:

Đối với một hạt tích điện di chuyển trên từ trường, .

Động năng được thực hiện bởi từ trường là .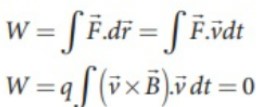

Vì vuông góc với và do đó . Điều này có nghĩa là lực Lorentz không hoạt động trên hạt. Từ định lý động năng công việc, (Tham khảo phần 4, tiêu chuẩn XI Tập I).

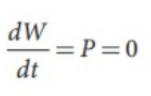
Vì,  và  vuông góc với nhau. Góc giữa lực Lorentz và vận tốc của hạt tích điện là 90º. Do đó, lực Lorentz thay đổi hướng của vận tốc, nhưng không thay đổi độ lớn của vận tốc. Do đó lực Lorentz không hoạt động và cũng không làm thay đổi động năng của hạt.

3.2. Chuyển động của một hạt tích điện trong từ trường đồng nhất:

Ví dụ: Một electron chuyển động vuông góc với từ trường đồng nhất 0,500 T trải qua chuyển động tròn bán kính 2,80 mm. Tốc độ của electron là gì?

Lời giải:

Điện tích của electron q = -1,60 × 10-19 C

⟹ |q| = 1,60 ×10−19 C

Độ lớn của từ trường B = 0,500 T

Khối lượng của electron, m = 9, 11 × 10-31 kg

Bán kính quỹ đạo, r = 2, 50 mm = 2, 50 × 10-3 m

Vận tốc của electron, v = |q| rB / m

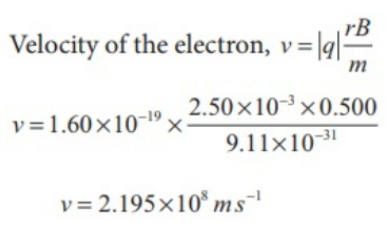
v = 2.195 ×108 m s−1

Ví dụ: Một proton di chuyển trong một từ trường đồng nhất có cường độ từ 0,500 T được định hướng dọc theo trục x. Tại thời điểm ban đầu, t = 0 s, proton có vận tốc  . Tìm:

(a) Tại thời điểm ban đầu, gia tốc của proton là gì.

(b) Là đường dẫn tròn hay xoắn ốc?. Nếu là xoắn ốc, tính bán kính của quỹ đạo xoắn ốc và cũng tính cao độ của chuỗi xoắn (Lưu ý: Cao độ của chuỗi xoắn là khoảng cách di chuyển dọc theo trục xoắn trên mỗi vòng quay).

Lời giải:

Cao độ của chuỗi xoắn là khoảng cách di chuyển dọc theo trục x trong thời gian T, là P = vx T

Nhưng thời gian

Proton trải qua gia tốc đáng kể trong từ trường, do đó cao độ của chuỗi xoắn lớn hơn gần sáu lần so với bán kính của chuỗi xoắn.

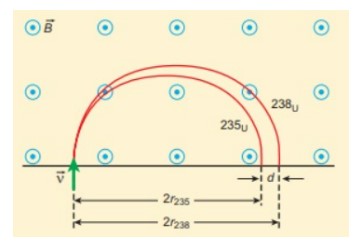
Ví dụ: Hai đồng vị ion hóa đơn lẻ của urani   và  (đồng vị có cùng số nguyên tử nhưng số khối khác nhau) được gửi với vận tốc 1,00 × 105 m s-1 vào từ trường có cường độ 0,500 T bình thường. Tính khoảng cách giữa hai đồng vị sau khi chúng hoàn thành một hình bán nguyệt. Đồng thời tính toán thời gian thực hiện bởi mỗi đồng vị để hoàn thành một đường bán nguyệt. (Lưu ý: khối lượng của các đồng vị: m235 = 3, 90 x 10-25 kg và m238 = 3, 95 x 10-25 kg)

Lời giải:

Vì các đồng vị bị ion hóa đơn lẻ, chúng có điện tích bằng nhau bằng điện tích của electron, q = – 1,6 × 10-19 C. Khối lượng uranium    và lần lượt là 3,90 × 10-25 kg và 3,95 × 10-25 kg. Từ trường áp dụng, B = 0, 500 T. Vận tốc của electron là 1, 00 × 105 m s-1, sau đó

(a) the radius of the path of 23592U is r235

Đường kính của hình bán nguyệt do là  = 98,8 cm

Do đó, khoảng cách tách giữa các đồng vị là Δd =  = 1,2cm

(b) Thời gian thực hiện bởi mỗi đồng vị để hoàn thành một đường bán nguyệt là:

Lưu ý rằng mặc dù sự khác biệt giữa khối lượng của hai đồng vị là rất nhỏ, sự sắp xếp này giúp chúng ta chuyển đổi sự khác biệt nhỏ này thành một khoảng cách tách dễ đo được. Sự sắp xếp này được gọi là máy quang phổ khối. Máy quang phổ khối được sử dụng trong nhiều lĩnh vực trong khoa học, đặc biệt là trong y học, khoa học vũ trụ, địa chất, v.v. Ví dụ, trong y học, các bác sĩ gây mê sử dụng nó để đo khí hô hấp và nhà sinh học sử dụng nó để xác định các cơ chế phản ứng trong quang hợp.