Đề thi giữa học kì 2 môn Toán 9 năm 2023 – 2024 có đáp án

1. Nội dung cần ôn tập khi thi giữa học kì 2 môn Toán 9 năm 2023 – 2024? 

Để ôn tập cho kỳ thi giữa học kỳ 2 môn Toán 9 năm 2023-2024, bạn cần ôn tập các chủ đề sau:

– Đại số: Tính chất của phép cộng, phép trừ, phép nhân và phép chia trong các số nguyên và phân số; giải các phương trình bậc nhất, bậc hai, và hệ phương trình đơn giản; giải các bài toán liên quan đến đại số.

– Hình học: Tính chất của các đường thẳng, góc, tam giác, hình vuông, hình chữ nhật, hình tròn, hình trụ và hình cầu; giải các bài toán liên quan đến hình học.

– Giải tích: Tính toán đạo hàm và tích phân của các hàm số đơn giản; áp dụng các phương pháp giải tích trong giải các bài toán liên quan đến tốc độ, gia tốc, tích phân, đạo hàm, và bài toán giá trị lớn nhất, giá trị nhỏ nhất.

– Xác suất và thống kê: Tính toán xác suất, biểu đồ, phân tích dữ liệu thống kê và giải các bài toán liên quan đến xác suất và thống kê.

Ngoài ra, bạn cũng nên luyện tập giải các đề thi mẫu, tập trung vào các dạng bài toán khó, trang bị cho mình các kỹ năng giải toán và cách suy nghĩ logic để giải quyết các bài toán phức tạp. Cuối cùng, hãy đọc kỹ các đề thi để hiểu rõ hơn yêu cầu của từng câu hỏi và cách trả lời cho phù hợp.

2. Một số lưu ý khi làm Đề thi giữa học kì 2 môn Toán 9 năm 2023 – 2024?

Để làm tốt đề thi giữa học kì 2 môn Toán 9 năm 2023 – 2024, bạn có thể tham khảo một số lưu ý sau đây:

– Học tất cả các kiến thức cơ bản: Để làm tốt đề thi, bạn nên học tất cả các kiến thức cơ bản của môn Toán, đặc biệt là những khái niệm quan trọng. Hãy đảm bảo rằng bạn đã hiểu rõ từng bước và công thức cần thiết để giải quyết các bài toán.

– Ôn tập các bài tập trọng tâm: Bạn nên ôn tập các bài tập trọng tâm, bao gồm các bài tập có độ khó từ trung bình đến khó. Điều này sẽ giúp bạn làm quen với cách giải quyết các bài tập khó hơn và đảm bảo bạn đã nắm chắc kiến thức cần thiết.

– Làm các bài tập mẫu và đề thi thử: Hãy làm các bài tập mẫu và đề thi thử để nâng cao kỹ năng giải toán và rèn luyện kỹ năng làm bài trong thời gian giới hạn. Điều này sẽ giúp bạn quen với cấu trúc đề thi và cải thiện khả năng làm bài của mình.

– Chú ý đến các dạng bài toán: Trong đề thi, có nhiều dạng bài toán khác nhau và mỗi dạng đều có cách giải khác nhau. Bạn nên chú ý đến các dạng bài toán và phân tích cách giải của chúng để có thể giải quyết mọi bài toán được đưa ra.

– Tập trung vào từng câu hỏi: Để làm tốt đề thi, hãy tập trung vào từng câu hỏi một, đọc kỹ đề và hiểu rõ yêu cầu của từng câu hỏi. Sau đó, bạn có thể giải quyết từng câu hỏi một và không nên bỏ qua bất kỳ câu hỏi nào.

– Làm bài sạch sẽ và rõ ràng: Hãy làm bài sạch sẽ và rõ ràng, viết đúng và sạch chữ, đảm bảo rằng giáo viên có thể đọc được các câu trả lời của bạn. Nếu cần, hãy sử dụng bút chì để xóa những lỗi sai và viết lại.

3. Đề thi giữa học kì 2 môn Toán 9 năm 2023 – 2024 có đáp án mới nhất – Đề số 1:

Bài 1 (2,5 điểm)

Trong mặt phẳng tọa độ Oxy, cho Parabol và đường thẳng

1. Tìm tọa độ giao điểm của (P) và (Q).
2. Gọi A, B là hai giao điểm của (P) và (Q). Tính diện tích tam giác OAB,

Bài 2 (5,0 điểm)

Cho đường tròn tâm O đường kính AB. Dây CD vuông góc với AB tại E (E nằm giữa A và O; E không trùng  A, không trùng O). Lấy điểm M thuộc cung nhỏ BC sao cho cung MB nhỏ hơn cung MC. Dây AM cắt CD tại F. Tia BM cắt đường thẳng CD tại K.

1. Chứng minh tứ giác BMFE nội tiếp.
2. Chứng minh BF vuông góc với AK và EK.EF = EA.EB
3. Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK = IF.

Bài 3. (2,5 điểm) Với các số a, b, c > 0 và thỏa mãn a + b + c = 1

Chứng minh

Đáp án và Hướng dẫn làm bài
Câu 1:

a. Hoành độ giao điểm của (P) và (Q) là nghiệm của phương trình:

Đề thi Toán 9 Giữa học kì 2 năm 2023 có đáp án (50 đề)

b. Gọi A, B là hai giao điểm của (P) và )Q). Tính diện tích tam giác OAB.

Đề thi Toán 9 Giữa học kì 2 năm 2023 có đáp án (50 đề)

Đề thi Toán 9 Giữa học kì 2 năm 2023 có đáp án (50 đề)

Câu 2:

Gọi số chi tiết máy mỗi tổ đã sản xuất được trong tháng đầu là x, y (Đề thi Toán 9 Giữa học kì 2 năm 2023 có đáp án (50 đề), chi tiết máy)

Vì trong tháng đầu, hai tổ sản xuất được 860 chi tiết máy nên ta có phương trình:

Đề thi Toán 9 Giữa học kì 2 năm 2023 có đáp án (50 đề)

Vì đến tháng thứ hai, tổ I vượt mức 15%, tổ II vượt mức 10%. Do đó, tháng thứ hai cả 2 tổ sản xuất được 964 chi tiết máy, nên ta có phương trình:

Đề thi Toán 9 Giữa học kì 2 năm 2023 có đáp án (50 đề)

Từ (1) và (2) ta có hệ phương trình:

Đề thi Toán 9 Giữa học kì 2 năm 2023 có đáp án (50 đề)

Đề thi Toán 9 Giữa học kì 2 năm 2023 có đáp án (50 đề)

Vậy trong tháng đầu, số chi tiết máy mỗi tổ đã sản xuất được lần lượt là: 360 và 500.

Câu 3:

Đề thi Toán 9 Giữa học kì 2 năm 2023 có đáp án (50 đề)

a. Chứng minh tứ giác BMFE nội tiếp.

Ta có Đề thi Toán 9 Giữa học kì 2 năm 2023 có đáp án (50 đề)

Nên 4 điểm E, F, M, B cùng thuộc đường tròn đường kính BF, suy ra tứ giác BMFE nội tiếp.

b. Chứng minh BF vuông góc với AK và EK.EF = EA.EB

Đề thi Toán 9 Giữa học kì 2 năm 2023 có đáp án (50 đề)

Nên F là trực tâm, suy ra Đề thi Toán 9 Giữa học kì 2 năm 2023 có đáp án (50 đề)

Đề thi Toán 9 Giữa học kì 2 năm 2023 có đáp án (50 đề)

c. Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK = IF.

4. Đề thi học giữa học kì 2 môn Toán 9 năm 2023 – 2024 có đáp án mới nhất – Đề số 2:

Phòng Giáo dục và Đào tạo …..

Đề thi Giữa học kì 2

Môn: Toán 9

Thời gian làm bài: 90 phút

(Đề 2)

I.PHẦN TRẮC NGHIỆM (2,0 điểm)

(Hãy chọn phương án đúng và viết chữ cái đứng trước phương án đó vào bài làm)

Câu 1. Rút gọn biểu thức :

Câu 2. Phương trình  có nghiệm là:

A.

B. x = 1 và y = -2

C. x = 1 và y = 2

D. x = -3 và y = 8

Câu 3. Đồ thị hàm số  đi qua điểm có tọa độ là

Câu 4. Phương trình nào sau đây có ít nhất một nghiệm nguyên?

A. x2 – x + 1 = 0

B. 9x2 – 6x + 1 = 0

C.

D. 16x2 – 1 = 0

Câu 5. Phương trình (m là tham số) có nghiệm khi và chỉ khi:

A. m < 4

B. m > -2

C.

D.

Câu 6. Cho đường tròn tâm (O; R) và dây cung BC = R. Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau tại A. Khi đó bằng:

Câu 7. Cho tam giác đều MNE ngoại tiếp đường tròn bán kính 1 cm. Diện tích của tam giác MNE bằng:

A.

B.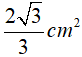

C.

D. 5cm2

II.PHẦN TỰ LUẬN (8,0 điểm)

Câu 1 (1,5 điểm)

a. Rút gọn biểu thức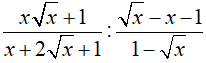

b. Cho hàm số y = -3x – m + 1, với m là tham số. Xác định giá trị của m để đồ thị hàm số y = -3x – m + 1 đi qua gốc tọa độ O

Câu 2 (1,75 điểm)

a. Giải phương trình x² – x – 6 = 0

b. Cho phương trình mx2 – 2(m-1)x + m = 0 (1), với m là tham số. Xác định giá trị của m để phương trình (1) có hai nghiệm phân biệt.

Câu 3 (0,75 điểm) Giải hệ phương trình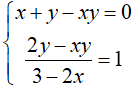

Câu 4 (3,25 điểm) Cho đường tròn (O) đường kính BC. Trên đường tròn (O) lấy điểm A sao cho AB < AC. Trên OC lấy điểm M sao cho M nằm giữa O và C. Qua M kẻ đường thẳng vuông góc với OC cắt tia đối của tia AB tại N, cắt AC tại F. Đường thẳng NM cắt đường tròn (O) tại F và K (F nằm giữa E và N)

a. Chứng minh bốn điểm A, B, M, E cùng thuộc một đường tròn và chứng minh bốn điểm N, A, M, C cùng thuộc một đường tròn.

b. Vẽ tiếp tuyến tại A của đường tròn (O) cắt MN tại H. Chứng minh tam giác là tam giác cân.

c. Gọi giao điểm thứ hai của NC với đường tròn (O) là D. Chứng minh HD là

tiếp tuyến của đường tròn (O).

Câu 5 (0,75) Giải phương trình

5. Một số tip đạt điểm cao khi làm Đề thi giữa học kì 2 môn Toán 9 năm 2023 – 2024?

Để đạt điểm cao trong đề thi giữa học kì 2 môn Toán lớp 9, bạn có thể áp dụng một số tips sau:

– Làm quen với đề thi: Bạn nên tham khảo các đề thi mẫu, bài tập và kiểm tra của năm học trước để làm quen với cấu trúc đề thi và các dạng bài tập.

– Học tất cả các chương trình: Học và luyện tập đầy đủ toàn bộ nội dung của chương trình môn Toán lớp 9 để đảm bảo rằng bạn đã hiểu hết các kiến thức cơ bản trước khi bước vào làm đề thi.

– Học cách giải các bài toán: Bạn cần học cách đọc đề bài, tìm hiểu các thông tin cần thiết, xác định dạng bài toán và sử dụng các phương pháp giải phù hợp để trả lời câu hỏi.

– Luyện tập giải các bài tập: Luyện tập giải các bài tập liên quan đến chương trình để củng cố kiến thức và rèn luyện kỹ năng giải quyết các bài tập.