Công thức tính và cách tính đường chéo hình vuông chuẩn

1. Tìm hiểu về hình vuông:

Hình vuông là tứ giác có 4 góc vuông và 4 cạnh bằng nhau.

Ta có thể nhận biết hình vuông qua một số dấu hiệu sau:

– Hình vuông cũng chính là hình chữ nhật có hai cạnh kề bằng nhau.

– Hai đường chéo của hình chữ nhật vuông góc với nhau là hình vuông

– Hình thoi có 1 góc vuông

– Hình thoi có hai đường chéo bằng nhau

Tính chất của hình vuông:

– Có 2 cặp cạnh song song.

– Có 4 cạnh bằng nhau.

– Hai đường chéo hình vuông bằng nhau, vuông góc và giao nhau tại trung điểm của mỗi đường.

– Giao điểm hai đường chéo của hình vuông là tâm của đường tròn nội tiếp và ngoại tiếp.

– Giao của các đường phân giác, trung tuyến, trung trực đều trùng tại một điểm.

– Một đường chéo sẽ chia hình vuông thành hai phần có diện tích bằng nhau.

– Có một đường tròn nội tiếp và ngoại tiếp, đồng thời tâm của cả hai đường tròn trùng nhau và là giao điểm của hai đường chéo của hình vuông.

– Hình vuông có tất cả tính chất của hình chữ nhật và hình thoi.

2. Công thức tính đường chéo của hình vuông:

Đường chéo hình vuông là 2 đường thẳng nối 2 đỉnh không kề nhau của hình vuông, vuông góc và giao nhau tại trung điểm của mỗi đường.

Trong một hình vuông có 2 đường chéo. Theo tính chất của hình vuông, đường chéo của hình vuông có tính chất: hai đường chéo hình vuông bằng nhau và một đường chéo hình vuông sẽ chia hình vuông thành hai phần có diện tích bằng nhau chính là 2 tam giác vuông cân. Như vậy thì đường chéo hình vuông chính là cạnh huyền của 2 tam giác vuông cân đó. Để tính đường chéo hình vuông ta áp dụng định lý Pi-ta-go trong tam giác vuông.

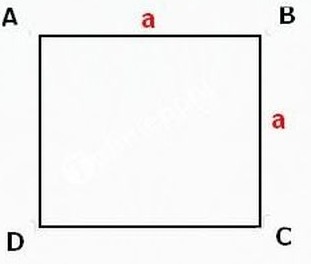
Gọi cạnh hình vuông là a, đường chéo của hình vuông là b, áp dụng định lý Pytago, ta có:

Đường chéo của hình vuông là

Các lưu ý khi tính đường chéo hình vuông:

Khi làm bài tập tính đường chéo hình vuông, ta cần xác định đúng tính chất của một hình vuông, tính chất của đường chéo hình vuông. Xem các dạng toán liên quan như Chu vi hình vuông, diện tích hình vuông,… để hiểu rõ về hình vuông một cách chính xác nhất. Ngoài ra:

– Nhớ kỹ và áp dụng đúng công thức.

– Sử dụng máy tính cầm tay để kết quả tính toán chắc chắn hơn.

– Sử dụng máy tính cầm tay như một công cụ hỗ trợ

– Các đại lượng phải cùng đơn vị đo.

– Tránh ghi sai đơn vị tính.

3. Ví dụ minh họa cách tính đường chéo hình vuông:

Ví dụ 1: Một hình vuông có cạnh bằng 3cm. Đường chéo của hình vuông đó bằng: 6cm, √18cm, 5cm, hay 4cm?

Bài giải:

Áp dụng định lí Pi-ta-go trong hình vuông ABC, ta có:

AC² = AB² + BC² = 3² + 3² = 18

=> AC = √18 cm

Vậy đường chéo của hình vuông bằng √18 cm .

Ví dụ 2: Đường chéo của một hình vuông bằng 2dm. Cạnh của hình vuông đó bằng: 1dm, 3/2dm, √2dm hay 4/3dm?

Bài giải:

Tương tự, cũng áp dụng định lí Py-ta-go vào tam giác vuông ABC, nhưng bài này cho độ dài đường chéo, tức AC = 2dm, tính cạnh AB.

Ta có: AC² = AB² + BC² = 2AB (vì AB = BC)

=> AB² = AC²/2 = 2²/2 = 2

=> AB = √2

Vậy cạnh hình vuông bằng √2dm.

4. Bài tập tính đường chéo hình vuông:

Bài 1: Cho hình vuông ABCD có cạnh a = 5 cm, tính đường chéo AC và BD của hình vuông này

Đáp án: áp dụng công thức tính đường chéo trong hình vuông

Đường chéo bằng cạnh x căn hai

Với a = 5 ta có đường chéo AC = 5 cm x √2

Đường chéo BD = 5 cm x √2

Do cạnh a = 5 cm ta có thể tính được giá trị chính xác của đường chéo AC và BD trong hình vuông ABCD bằng 5√2

Bài 2: Tính độ dài các cạnh trong hình vuông với MP = a căn 2, trong đó D là đường chéo A là các cạnh của hình vuông đáp án giả sử hình vuông ABCD ta biết đường chéo có độ dài bằng 10√2 cm

Đáp án: Tính độ dài các cạnh trong hình vuông này ta cần áp dụng công thức tính đường chéo và quan hệ giữa đường chéo và các cạnh của hình vuông

Do đường chéo có độ dài bằng 10 căn 2 ta có thể suy ra đường chéo bằng cạnh x căn 2 m căn 2 bằng cạnh xcăn 2

Ta có cạnh của hình vuông ABCD bằng cạnh bằng 10 cm

Vậy độ dài cạnh trong hình vuông ABCD là 10 cm

Bài 3: Cho tam giác vuông cân ABC, vuông tại A, có cạnh AC bằng 7 cm.

Đáp án: 

Để tính độ dài đường chéo của hình vuông ABCD M vẽ ta cần biết quan hệ giữa đường chéo và cạnh trong hình vuông Cho tam giác ABC là tam giác vuông cân ta biết rằng đường cao AD của tam giác vuông cân sẽ chia đoạn AC thành hai phần bằng nhau

Vì vậy cạnh của hình vuông ABCD sẽ là một nửa cạnh AC vì AC = 7 cm ta có ab = ac/2 = 7 cm/2 = 3,5 cm

Bài 4: Cho hình vuông ABCD trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Chứng minh tứ giác EFGH là hình vuông

Đáp án:

Vì ABCD là hình vuông lên AB = BC = CD = DA nên góc A = góc B = góc C = góc D bằng 90 độ

Ta có AB = AE + EB

BC = BF + FC

CD = CG + DG

AD = DH+ AH

Mà AB = BC = CD = DA và AE = BF = CG = DH nên EB = CF = DG = AH

Xét tam giác AHE và tam giác BEF có góc A = góc B = 90 độ AH = BE, AE = EF do đó tam giác AHE = tam giác BEF

Suy ra cạnh HE = EF

Xét tam giác CFH và tam giác DGH có góc E và góc D bằng 90 độ

Do đó tam giác CFH  bằng tam giác DHG suy ra FG = GH

Tam giác CFM và tam giác AHE có góc C bằng góc A bằng 90 độ CF = AH, CG = AE

Do đó tam giác CFM = tam giác AHE suy ra FG = HE

Xét tứ giác EFGH ta có FG = HE = EF nên tứ giác EFGH là hình thoi

Lai có FEB cộng ESB = 90°. Mà AIH = EFB nên AEH + EFB = 90°. Ngoài ra AEH+ góc HEF + góc FEB bằng 180 độ suy ra góc HEF = 90°.

Mà hình thoi EFGH có một góc vuông lên hình thoi EFGH là hình vuông

Bài 5: Tính độ dài đường chéo hình vuông biết độ dài cạnh hình vuông là 10.

Đáp án:

Gọi độ dài đường chéo hình vuông trên là a (đk: a > 0, cm)

Áp dụng định lý Pitago, ta có độ dài đường chéo của hình vuông trên là:

a² = 2 x 10² = 200

⇔ a = 10√2 (tmdk)

Độ dài đường chéo của hình vuông trên là 10√2 cm.

Bài 6: Cho hình vuông ABCD có cạnh có độ dài là 6 cm. Tính S hình vuông ABCD?

Đáp án:

Diện tích hình vuông ABCD là:

6 x 6 = 36 (cm²)

Đáp số: 36 cm²

Bài 7: Một hình vuông có cạnh bằng 3cm. Đường chéo của hình vuông đó bằng bao nhiêu?

Đáp án:

Áp dụng công thức, ta có:

AC² = AB² + BC² = 3² + 3² = 18

=> đường chéo hình vuông =  √18 cm

Bài 8: Cho tam giác vuông cân ABC tại A, có cạnh AC bằng 7cm. Để tính độ dài đường chéo của hình vuông ABCD mới vẽ, ta cần biết quan hệ giữa đường chéo và cạnh trong hình vuông.

Đáp án:

Do tam giác ABC là tam giác vuông cân, ta biết rằng đường cao AD của tam giác vuông cân sẽ chia đoạn AC thành hai phần bằng nhau. Vì vậy, cạnh của hình vuông ABCD sẽ là một nửa của cạnh AC.

Vì AC = 7cm, ta có:

Cạnh AB = AC / 2 = 7cm / 2 = 3.5cm

Bài 9. Cho hình vuông ABCD có cạnh a = 5cm, tính đường chéo AC, BD?

Bài 10. Cho hình vuông ABCD có đường chéo bằng 10√2 cm, tính độ dài các cạnh của hình vuông?

Bài 11. Cho tam giác vuông cân ABC tại A, có cạnh AC bằng 7cm. Vẽ hình vuông ABCD. Tính độ dài đường chéo của hình vuông ABCD mới vẽ