Bài viết dưới đây sẽ cung cấp công thức tính nhiệt lượng toả ra và các bài tập có đáp án sẽ giúp học sinh nắm vững công thức, từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi môn Vật Lí 8.
Mục lục bài viết
1. Nhiệt lượng toả ra là gì?
Nhiệt lượng toả ra là một khái niệm cực kỳ quan trọng và phổ biến trong vật lý, liên quan đến sự chuyển đổi và truyền đạt năng lượng từ một hệ thống đến môi trường xung quanh. Đây là một phần cơ bản của quá trình trao đổi năng lượng và sự chuyển động của nhiệt từ các vật thể có nhiệt độ cao đến vật thể có nhiệt độ thấp hơn.
Ở mức độ cơ bản, nhiệt lượng toả ra thường được diễn đạt thông qua các quá trình phát ra nhiệt từ một vật thể đến vật thể khác thông qua ba cơ chế chính: dẫn, phát sóng và tỏa nhiệt.
Đầu tiên, qua dẫn nhiệt, năng lượng nhiệt động từ các phân tử trong vật thể đang di chuyển qua các phân tử kề cận thông qua tác động của chúng lên nhau. Đây là lý do tại sao, khi bạn đặt một thanh kim loại vào lửa, phần cuối cùng của nó sẽ nhanh chóng trở nên nóng. Các phân tử nhiệt động của lửa chuyển giao nhiệt động cho phần kim loại còn lạnh.
Thứ hai, là phát sóng nhiệt. Điều này ám chỉ việc các vật thể phát ra nhiệt thông qua sóng điện từ. Ví dụ điển hình là mặt trời, nơi năng lượng từ hạt nhân được phát ra và truyền đến trái đất dưới dạng sóng điện từ.
Cuối cùng, tỏa nhiệt là quá trình mà một vật thể phát ra nhiệt lượng thông qua quá trình chuyển động của các phân tử của nó. Khi một vật thể có nhiệt độ cao hơn môi trường xung quanh, nó sẽ tỏa ra nhiệt lượng để cân bằng với môi trường đó. Đây là lý do tại sao các vật thể có nhiệt độ cao sẽ nguội dần khi đặt trong môi trường có nhiệt độ thấp hơn.
Nhiệt lượng toả ra đóng vai trò quan trọng trong nhiều lĩnh vực của cuộc sống hàng ngày và các lĩnh vực khoa học khác nhau như công nghiệp, vật lý, sinh học, và ngay cả trong việc thiết kế và hiểu biết về hệ thống năng lượng tự nhiên như hệ mặt trời hay hệ nhiệt động lực trái đất. Việc hiểu và vận dụng khái niệm này không chỉ giúp chúng ta hiểu rõ hơn về cách mà năng lượng di chuyển, mà còn là yếu tố quan trọng trong việc tối ưu hóa sử dụng năng lượng và thiết kế các hệ thống hiệu suất cao.
2. Công thức tính nhiệt lượng toả ra:
– Khi một vật hạ nhiệt độ từ t1 xuống t2 nó sẽ tỏa ra nhiệt lượng là:
Qtỏa = m.c. Δt, hay Qtỏa = m.c.(t1 – t2)
Trong đó:
+ Q: là nhiệt lượng tỏa ra của vật (J)
+ m: là khối lượng của vật (kg)
+ c: là nhiệt dung riêng của chất làm nên vật (J/kg.K)
+ Δt = t1 – t2: là độ giảm nhiệt độ của vật (°C hoặc °K)
– Lưu ý: Trong công thức nhiệt lượng tỏa ra thì nhiệt độ t2 luôn nhỏ hơn t1.
Từ công thức tính nhiệt lượng toả ra: Qtỏa = m.c.(t1 – t2), suy ra:
– Công thức tính khối lượng của vật: 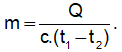
– Công thức tính nhiệt dung riêng của chất cấu tạo nên vật: 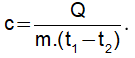
– Công thức tính độ giảm nhiệt độ của vật: 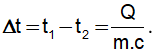
Ví dụ 1: Người ta thả một miếng đồng có khối lượng 0,5 kg vào nước. Miếng đồng nguội đi từ 120°C xuống 60°C. Lấy nhiệt dung riêng của đồng là 380 J/kg.K. Tính nhiệt lượng miếng đồng toả ra.
Tóm tắt:
m = 0,5 kg
t1 = 120°C, t2 = 60°C
c = 380 J/kg.K
Qtoả = ?
Giải:
Nhiệt lượng miếng đồng toả ra là:
Qtỏa = m.c.(t1 – t2) = 0,5.380.(120-60) = 11400 (J).
Ví dụ 2: Thả một quả cầu nhôm được nung nóng tới 100°C vào một ca nước ở 20°C. Sau một thời gian nhiệt độ của cả nhôm và nước là 25°C. Biết nhiệt lượng của quả cầu nhôm toả ra là 9900 J, tính khối lượng của quả cầu nhôm. Lấy nhiệt dung riêng của nhôm bằng 880J/kg.K.
Tóm tắt:
Nhôm: t1 = 100°C, t2 = 25°C, c = 880 J/kg.K, Qtoả = 9900 J
m = ?
Giải:
Khối lượng của quả cầu nhôm là:
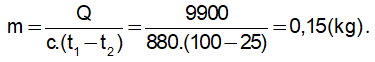
3. Bài tập vận dụng:
Bài 1: Một ấm nước bằng đồng khối lượng 300g chứa 1 lít nước. Tính nhiệt lượng cần thiết để đun nước trong ấm từ 150 C đến 1000 C. Biết nhiệt dung riêng của nước là 4200 J/kg.K, của đồng là 380 J/kg.K.
Nhiệt lượng cần cung cấp để ấm đồng tăng nhiệt độ từ 150C đến 1000C là:
Q1 = m1.c1.(t2 – t1) = 0,3.880.(100 – 15) = 9690 (J)
Nhiệt lượng cần cung cấp để nước tăng nhiệt độ từ 150C đến 1000C là:
Q2 = m2.c2.(t2 – t1) = 1.4200.(100 – 15) = 357000 (J)
Nhiệt lượng cần cung thiết để đun nước trong ấm 150C đến 1000C là:
Q = Q1 + Q2 = 9690 + 357000 = 366690 (J)
Bài 2: Môt khối lượng nước 25 kg thu được một nhiệt lượng 1050 kJ thì nóng lên tới 300C. Tính nhiệt độ ban đầu của nước.
Gọi t1 là nhiệt độ ban đầu của nước
Nhiệt lượng cần cung cấp cho nước là:
Q = m.c.(t2 – t1) = m.c.(30 – t) = 1050.103 (J)
=> t = 30 – 1050.103m.c = 30 – 1050.10325.4200 = 200C
Bài 3: Đặt một cái ấm nhôm có khối lượng 400 gam chứa 2 lít nước sôi 1000C lên trên bàn để cho nước nguội đi. Sau 1h30 phút thì nước trong ấm có nhiệt độ bằng nhiệt độ 270C của không khí trong phòng. Hỏi không khí trong phòng đã nhận bao nhiêu nhiệt lượng từ ấm truyền sang
Lúc đầu, cái ấm và nước chứa bên trong có nhiệt độ 1000C. Khi có cân bằng nhiệt thì nhiệt độ của cái ấm, của nước trong ấm và của không khí trong phòng là bằng nhau.
Nhiệt lượng nước tỏa ra là:
Q1 = m1.c1.Δt = 2.4200.(100 – 27) = 613200 J
Nhiệt lượng mà nhôm tỏa ra là:
Q2 = m2.c2.Δt = 0,4.880.(100 – 27) = 25696 (J)
Nhiệt lượng không khí nhận vào bằng nhiệt lượng của ấm nhôm và nước tỏa ra:
Q = Q1 + Q2 = 613200 + 25696 = 638896 (J)
Bài 4: Tại xưởng rèn, một bác thợ rèn nhúng con dao bằng thép có khối lượng 2,5kg đang nóng đỏ ở nhiệt độ 9000 C vào trong bể nước lạnh. Nước trong bể có thể tích 200 lít và có nhiệt độ bằng với nhiệt độ ngời trời 270 C. Bỏ qua sự truyền nhiệt cho thành bể và môi trường xung quanh. Hãy tính nhiệt độ của con dao khi có sự cân bằng nhiệt.
Gọi t là nhiệt độ khi có sự cân bằng nhiệt.
Nhiệt lượng do con dao bằng thép tỏa ra là: Q1 = m1.c1.(t1 – t)
Nhiệt lượng do nước thu vào là: Q2 = m2.c2.(t – t2)
Vì bỏ qua sự trao đổi nhiệt với môi trường nên nhiệt lượng mà nước thu vào bằng nhiệt lượng do dao bằng thép tỏa ra.
Ta có: Q1 = Q2
=> m1.c1.(t1 – t) = m2.c2.(t – t2)
<=> (m1.c1 + m2.c2).t = m1.c1.t1 + m2.c2.t2
<=> t = m1.c1.t1+m2.c2.t2m1.c1+m2.c2 = 2,5.460.900+200.4200.272,5.460+300.4200 = 28,20C
Bài 5: Một chậu bằng nhôm khối lượng 500g đựng 2 lít nước sôi. Phải thêm vào chậu bao nhiêu lít nước ở 200C để có nước ở 350C? Biết nhiệt dung riêng của nước là 4200 J/kg.K, của nhôm là 880 J/kg.K
Gọi m là khối lượng cần đổ thêm vào.
Nhiệt độ của nước sôi là 1000C => t1 = 1000C
Nhiệt lượng do chậu nhôm tỏa ra là:
Q1 = m1.c1.(t1 – t) = 0,5.880.(100 – 35) = 26000 (J)
Nhiệt lượng do nước trong chậu tỏa ra là:
Q1 = m2.c2.(t1 – t) = 2.4200.(100 – 35) = 546000 (J)
Nhiệt lượng do lượng nước cần đổ thêm nhận vào là:
Q3 = m.c2.(t – t2) = m.4200.(35 – 20) = 63000.m (J)
Phương trình cân bằng nhiệt: Q1 + Q2 = Q3
=> 26000 + 546000 = 63000.m
=> m = 9,1 (kg)
Vậy lượng nước cần đổ thêm vào là 9,1 kg hay 9,1 lít
Bài 6: Người ta thả một miếng nhôm khối lượng 0,5kg vào 500g nước. Miếng nhôm nguội đi từ 80°C xuống 20°C. Hỏi nước nhận được một nhiệt lượng bằng bao nhiêu và nóng lên thêm bao nhiêu độ? Cho biết nhiệt dung riêng của nhôm là 880J/kg.K; của nước là 4200J/Kg.K.
Hướng dẫn:
Nhiệt lượng nhôm toả ra khi hạ nhiệt độ từ 80°C xuống 30°C là :
Q1 = m1.c1.Δt1 = 0,5.880.(80 – 20) = 22000 (J)
Nhiệt lượng nước thu vào bằng nhiệt lượng đồng toả ra ta có :
Q2 = m2.c2.Δt2 = Q1= 22000(J)
Nước nóng lên thêm là: Δt2 = Q2m2.c2 = 220000,5.4200 = 10,5°C




