Công thức tính khoảng cách giữa đường thẳng và mặt phẳng song song

1. Công thức tính khoảng cách giữa đường thẳng và mặt phẳng song song:

Trong không gian Oxyz, cho đường thẳng d và mặt phẳng (P) song song với nhau. Đường thẳng d có chứa điểm M(α;β;γ). Mặt phẳng (P) có phương trình ax+by+cz+d=0. Khi đó, để tính khoảng cách giữa đường thẳng d và mặt phẳng (P), chúng ta có công thức sau:

Để tính khoảng cách giữa đường thẳng d và mặt phẳng (P), ta cần tìm vector pháp tuyến của mặt phẳng (P). Vector pháp tuyến của mặt phẳng (P) có thể được xác định bằng cách lấy hệ số của các biến x, y, và z trong phương trình mặt phẳng (P). Vì mặt phẳng (P) đã được cho là song song với đường thẳng d, nên vector pháp tuyến cũng chính là vector chỉ phương của đường thẳng d.

Sau khi đã xác định được vector pháp tuyến của mặt phẳng (P), ta có thể tính khoảng cách giữa đường thẳng d và mặt phẳng (P) bằng cách sử dụng công thức:

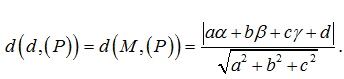
Trong đó, (x_0, y_0, z_0) là tọa độ của điểm M trên đường thẳng d, và (a, b, c) là vector pháp tuyến của mặt phẳng (P).

Đây là công thức cơ bản để tính khoảng cách giữa đường thẳng và mặt phẳng trong không gian Oxyz. Việc áp dụng công thức này sẽ giúp chúng ta xác định được khoảng cách giữa đường thẳng d và mặt phẳng (P) một cách chính xác và hiệu quả.

2. Ví dụ minh họa:

Ví dụ 1: Cho hình chóp tứ giác đều S.ABCD có AB = SA = 2a . Khoảng cách từ đường thẳng AB đến (SCD) bằng bao nhiêu?

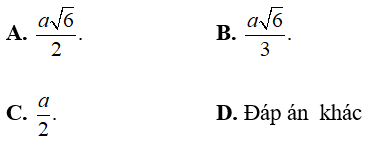
Hướng dẫn giải

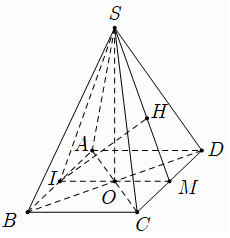
Gọi O là giao điểm của AC và BD; gọi I và M lần lượt là trung điểm cạnh AB và CD. Khi đó; IM // AD //BC

Do S.ABCD là hình chóp tứ giác đều có O là tâm của hình vuông nên SO ⊥ (ABCD) .

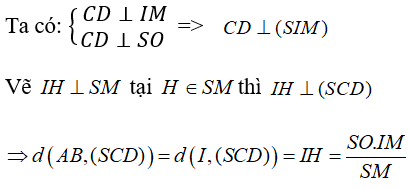
+ Do tam giác SAB là đều cạnh 2a

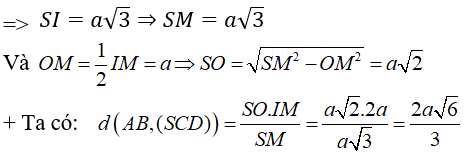
Chọn đáp án D

Ví dụ 2: Cho hình chóp S. ABCD có SA ⊥ (ABCD), đáy ABCD là hình thang vuông tại A và B; AB = a. Gọi I và J lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa đường thẳng IJ và (SAD)

Hướng dẫn giải

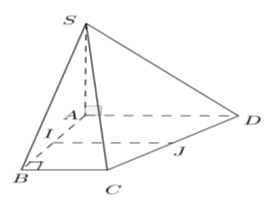
Chọn C

Ta có: I và J lần lượt là trung điểm của AB và CD nên IJ là đường trung bình của hình thang ABCD

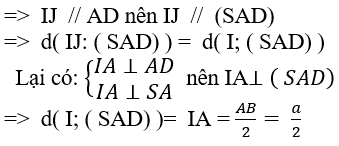
Ví dụ 3: Cho hình thang vuông ABCD vuông ở A và D; AD = 2a. Trên đường thẳng vuông góc tại D với (ABCD) lấy điểm S với SD = a√2. Tính khỏang cách giữa đường thẳng CD và (SAB).

Hướng dẫn giải

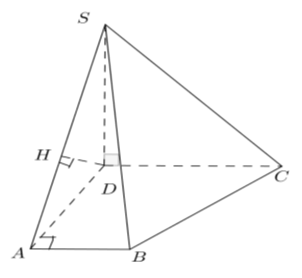
Chọn A

Vì DC // AB nên DC // (SAB)

⇒ d(DC; (SAB)) = d(D; (SAB))

Kẻ DH ⊥ SA

Do AB ⊥ AD và AB ⊥ SA nên AB ⊥ (SAD)

⇒ DH ⊥ AB lại có DH ⊥ SA

⇒ DH ⊥ (SAB)

Nên d(CD; (SAB)) = DH.

Trong tam giác vuông SAD ta có:

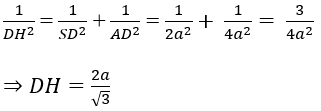
Ví dụ 4: Cho hình chóp O.ABC có đường cao OH = 2a/√3 . Gọi M và N lần lượt là trung điểm của OA và OB. Khoảng cách giữa đường thẳng MN và (ABC) bằng:

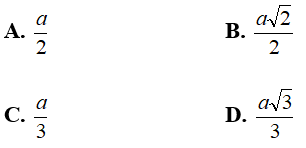
Hướng dẫn giải

Chọn D

Vì M và N lần lượt là trung điểm của OA và OB nên

MN // AB

⇒ MN // (ABC)

Khi đó, ta có:

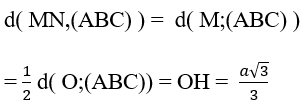
(vì M là trung điểm của OA).

3. Bài tập vận dụng:

Câu 1: Cho hình chóp tứ giác đều S.ABCD có đường cao SO = 2, mặt bên hợp với mặt đáy một góc 60°. Khi đó khoảng cách giữa hai đường thẳng AB và (SCD) bằng

Lời giải:

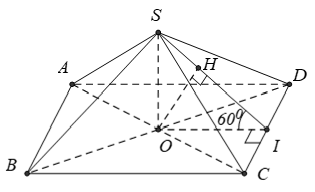
+ Gọi I là trung điểm của CD . Ta có:

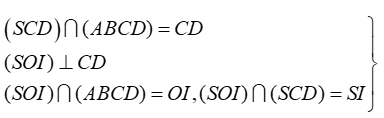
⇒ ((SCD), (ABCD)) = (OI, SI) = 60°

+ Ta có: AB // CD nên AB // (SCD)

⇒ d(AB, (SCD)) = d(A, ( SCD)) = 2.d(O, (SCD))

+ Trong mp (SOI) , gọi H là hình chiếu vuông góc của O lên SI

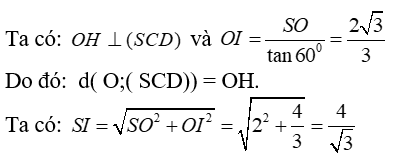
+ Tam giác SOI vuông tại O, có đường cao OH nên

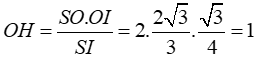
Do đó: d(AB; (SCD)) = 2d(O; (SCD)) = 2.OH = 2.1 = 2

Chọn B

Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Biết hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy và SA = a√2. Gọi E là trung điểm AD. Khoảng cách giữa AB và (SOE) là

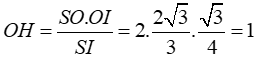
Lời giải:

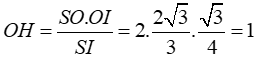
+ Vì hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy .

mà (SAB) ∩ (SAD) = SA

⇒ SA ⊥ (ABCD) .

+ Do E là trung điểm của AD khi đó

Tam giác ABD có EO là đường trung bình

⇒ EO // AB ⇒ AB // (SOE)

⇒ d(AB, (SOE)) = d(A; (SOE)) = AH

với H là hình chiếu của A lên SE.

Câu 3: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1 (đvdt). Khoảng cách giữa AA’ và (BB’D’) bằng:

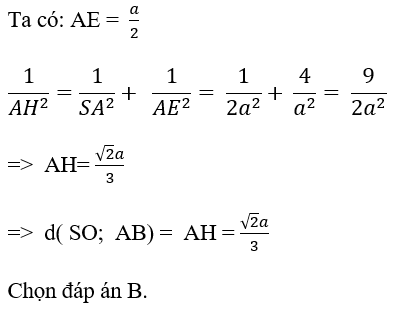
Lời giải:

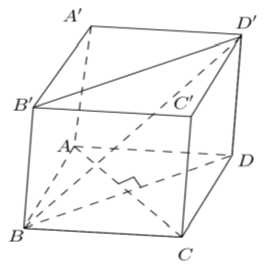
Chọn B

Ta có: AA’ // BB’ mà BB’ ⊂ ( BDD’B’)

⇒ AA’ // (BDD’B’)

⇒ d( AA’; (BD’B’)) = d(A; (BDD’B’)

Gọi O là giao điểm của AC và BD

⇒ AO ⊥ (BDD’B’) (tính chất hình lập phương)

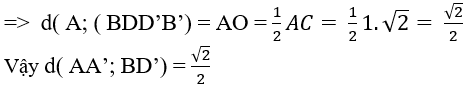
Câu 4: Cho hình chóp S.ABCD có SA ⊥ (ABCD) đáy ABCD là hình chữ nhật với AC = a√5 và BC = a√2. Tính khoảng cách giữa (SDA) và BC?

Lời giải:

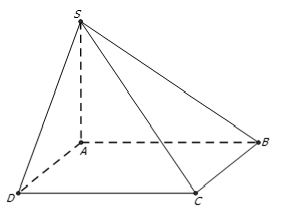
+ Ta có: BC // AD nên BC // (SAD)

⇒ d(BC; (SAD)) = d(B; SAD))

+ Ta chứng minh BA ⊥ (SAD) :

Do BA ⊥ AD (vì ABCD là hình chữ nhật)

Và BA ⊥ SA (vì SA ⊥ (ABCD))

⇒ BA ⊥ (SAD)

⇒ d(B; (SAD)) = BA

Áp dụng định lí Pytago trong tam giác vuông ABC có:

AB2 = AC2 – BC2 = 5a2 – 2a2 = 3a2

⇒ AB = √3 a

⇒ d(CB; (SAD)) = AB = √3 a

Đáp án D

Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và AB = 2a; BC = a . Các cạnh bên của hình chóp bằng nhau và bằng a√2 . Gọi E và F lần lượt là trung điểm của AB và CD; K là điểm bất kỳ trên BC. Khoảng cách giữa hai đường thẳng EF và (SBK) là:

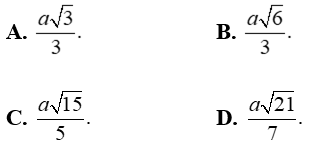
Lời giải:

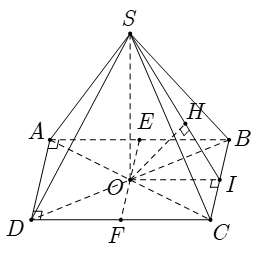
Gọi O là giao điểm của AC và BD; I là trung điểm cạnh BC

+ Do SA = SB = SC = SD và OA = OB = OC = OD nên SO ⊥ (ABCD)

+ Ta chứng minh BC ⊥ (SOI)

– Tam giác SBC cân tại S có SI là đường trung tuyến nên đồng thời là đường cao: BC ⊥ SI (1).

– Lại có: BC ⊥ SO (vì SO ⊥ (ABCD)) (2)

Từ ( 1) và ( 2) suy ra: BC ⊥ (SOI)

Mà OH ⊂ (SOI) nên BC ⊥ OH

⇒ OH ⊥ (SBC)

Do EF // BK nên EF // (SBK)

⇒ d(EF; (SBK)) = d(O; (SBK)) = OH

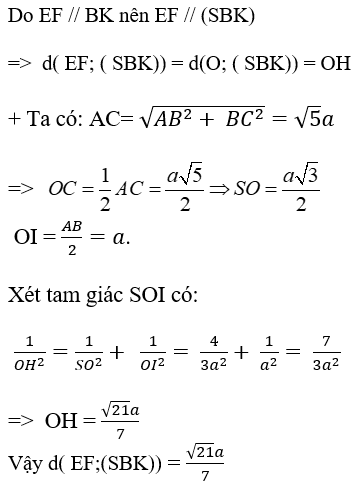
Chọn đáp án D.

Câu 6: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B; AB= a cạnh bên SA vuông góc với đáy và SA = a√2. Gọi M và N lần lượt là trung điểm của AB; AC. Khoảng cách giữa BC và (SMN) bằng bao nhiêu?

Lời giải:

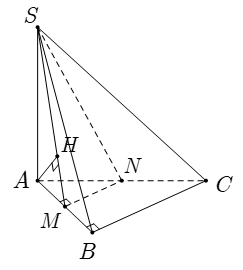
+ Tam giác ABC có MN là đường trung bình nên MN // BC

⇒ BC // (SMN) nên :

d(BC; (SMN)) = d(B; (SMN)) = d(A; (SMN))

Gọi H là hình chiếu vuông góc của A trên đoạn SM.

+ Ta chứng minh: MN ⊥ (SAM):

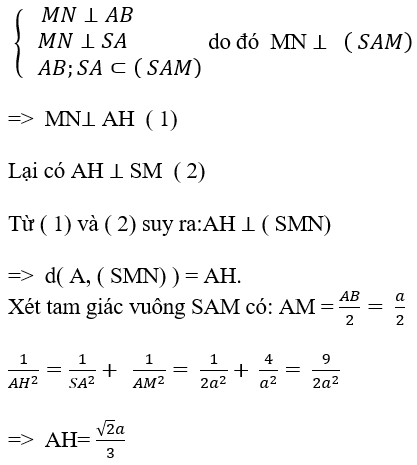
Chọn đáp án A

Câu 7: Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Các cạnh bên SA = SB = SC = SD = a√2. Khoảng cách giữa hai đường thẳng AD và (SBC) là:

Lời giải:

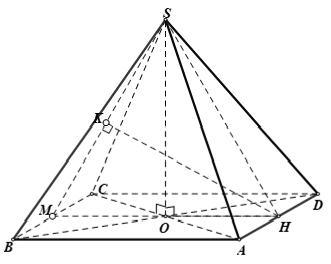
+ Do AD // BC nên AD // (SBC)

⇒ d (AD, (SBC)) = d(H; (SBC))

trong đó H là trung điểm AD.

+ Gọi M là trung điểm của BC và K là hình chiếu vuông góc của H lên SM

⇒ d(H; (SBC)) = HK.

+ Diện tích tam giác SMH là:

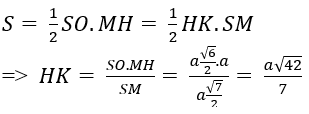
Chọn đáp án C

Câu 8: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SD = a√17/2 . Hình chiếu vuông góc H của đỉnh S lên mặt phẳng (ABCD) là trung điểm của cạnh AB. Gọi K là trung điểm của AD. Tính khoảng cách giữa hai đường HK và (SBD) theo a

Lời giải:

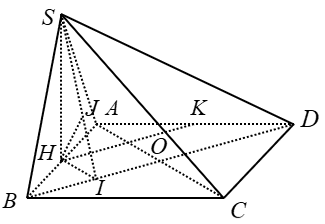
+ Ta có: H và K lần lượt là trung điểm của AB và AD nên HK là đường trung bình của tam giác ABD

⇒ HK // BD ⇒ HK // (SBD)

⇒ d(HK; (SBD)) = d(H, (SBD))

Kẻ HI ⊥ BD và HJ ⊥ SI

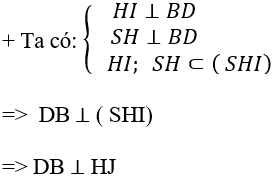
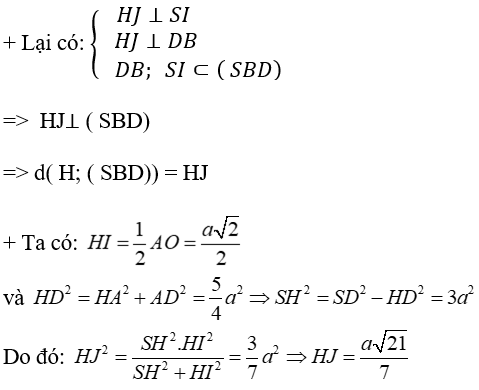
Chọn đáp án C

Câu 9: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và ∠ABC = 60° Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với đáy, góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 30°. Khoảng cách giữa hai đường thẳng CD và (SAB) theo a bằng:

Lời giải:

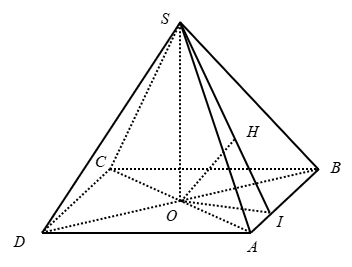
Gọi O là giao điểm của AC và BD

Kẻ: OI ⊥ AB; OH ⊥ SI

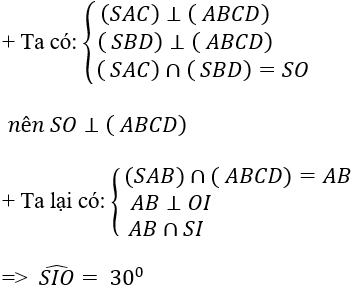
+ Do CD // AB nên CD // (SAB)

⇒ d(CD, (SAB)) = d(C; (SAB)) = 2d( O; (SAB))

Ta có: AB ⊥ SO , AB ⊥ OI ⇒ AB ⊥ (SOI) ⇒ AB ⊥ OH

Nên OH ⊥ (SAB) ⇒ d(O, (SAB)) = OH

Mà tam giác ACB cân tại B có ∠ABC = 60° nên tam giác ABC đều

⇒ OC = (1/2)AC = (1/2)AB = a/2 .

+ xét tam giác OAB có:

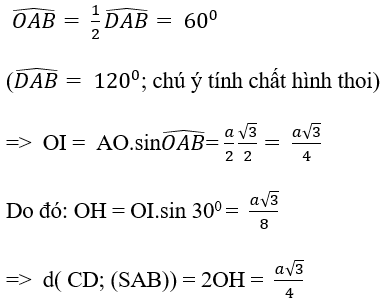
Chọn đáp án B